DecTree: a physics-based geochemical surrogate for surface complexation of uranium on clay

Geochemistry is usually the computational bottleneck in coupled reactive transport simulations, which hampers the complexity of the systems and of the processes they can investigate. In recent years, promising speedups have been obtained by substituting the numerical solution of geochemical models with approximated surrogates borrowed from artificial intelligence and machine learning (AI/ML). In the framework of the DONUT/EURAD project a set of benchmarks were defined to assess the performance and the accuracy of different surrogate approaches in settings relevant to the safety assessment of nuclear waste repositories, such as the surface complexation and exchange of U(VI) on clay. In this context, this work introduces am original surrogate modelling approach based on recursive partitioning of parameter space, which exploits prior domain knowledge for the training. The surrogate, which can be represented as a decision tree, hence the DecTree name, performs dimensionality reduction by identifying functional relationships between outputs and input variables using a straightforward non-monotonic extension of the Spearman's rank correlation coefficient. New predictions are then interpolated from the partitioned training data. Applied to a low-dimensional geochemical model, DecTree shows virtually no training time and excellent accuracy, ensuring a throughput of around 500 000 predictions per second on a single CPU core.

1 Introduction

Safety assessment of nuclear waste disposal sites requires large-scale reactive transport models (Jacques et al., 2021; Claret et al., 2022; Kolditz et al., 2023), which are however computationally intensive, with geochemistry usually representing the bottleneck from a numeric point of view. In recent years the scientific community has more and more explored different strategies in order to remove such computational bottleneck, especially by borrowing methods from Artificial Intelligence and Machine Learning (AI/ML) to obtain so called low-fidelity or surrogate models for geochemistry (Jatnieks et al., 2016; De Lucia et al., 2017; Laloy and Jacques, 2019; Guérillot and Bruyelle, 2020; Prasianakis et al., 2020; De Lucia and Kühn, 2021). The general idea is to pre-train a ML-model on a dataset obtained by classical numerical geochemical simulations and to employ the surrogate in coupled simulations, thus trading accuracy for improved performance. This approach has been particularly investigated in the context of nuclear waste disposal both in engineered barriers (cement) and in different types of host rock (e.g., Laloy and Jacques, 2022; Kolditz et al., 2023; Demirer et al., 2023; Hu and Pfingsten, 2023), but also for sensitivity analysis and uncertainty propagation (e.g., Turunen and Lipping, 2023; Sochala et al., 2024).

In the context of recently concluded DONUT european project (Claret et al., 2022), a benchmarking initiative has been initiated specifically to bring together expertise in geochemical modelling and in the application of ML/AI methods (Prasianakis et al., 2024a). The consortium defined and shared datasets depicting different geochemical systems of increasing complexity, solved with numerical geochemical simulators (Prasianakis et al., 2024a). These datasets served as test-bed for benchmarking different ML/AI regressors; participants to the initiative employed their method of choice, e.g., neural networks or gaussian processes, trying to reproduce the numerical data with the highest accuracy.

This study showcases an original entry to the aforementioned initiative, and specifically applied to the simple benchmark about surface complexation and exchange of uranium onto clay, introduced in Sect. 2.1. This entry is based on the same general principles of the DecTree numerical experiment (De Lucia and Kühn, 2021), however with a novel implementation and some key differences. For example, the original DecTree (version 1) approach consisted in a physics-based recursive partitioning of parameter space based on the identification of bijections among variables, both inputs, outputs and some user-defined engineered features derived from domain knowledge, such as law of mass action and mass conservation. Such non-linear partition is representable as a tree, where the edges are physically meaningful and thus interpretable conditions, and each leaf identifies a distinct parameter region in which each output variable can be regressed in terms of a minimal number of input variables. In this new application, detailed in Sect. 3.1, bijectivity has been replaced with the more general notion of functional association, and the computationally inexpensive heuristic adopted to identify it is discussed in Sect. 3.2. Finally the performance and the accuracy of this method in the application to the benchmark are discussed in Sect. 4.

2 Data: geochemical system and training data

2.1 The geochemical system: surface complexation of U(VI) on clay

The considered geochemical system represents the isotherm (25 °C) sorption of hexavalent uranium on clay as function depending on the initial total amount of U(VI) in the system and pH value. Batch (0D) geochemical models considering 1 g montmorillonite and 1 L of water in presence of a background NaCl concentration of 0.1 mol L⁻¹ were numerically simulated using widely adopted geochemical simulators; only the calculations and the resulting training and validation datasets obtained through Orchestra (Meeussen, 2003) were considered in this study. Surface complexation and cation exchange were modelled after Bradbury and Baeyens (1997) and the thermodynamical parameters for U(VI) sorption on montmorillonite were taken from Marques Fernandes et al. (2012, Table 2). The mineral phase metaschoepite (UO₃:2H₂O) was allowed to precipitate upon reaching saturation. Its dissolution reaction can be written:

$$\begin{array}{}\text{(R1)}& {\mathrm{UO}}_{\mathrm{3}}:\mathrm{2}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{2}{\mathrm{H}}^{+}\rightleftharpoons {\mathrm{UO}}_{\mathrm{2}}^{+\mathrm{2}}+\mathrm{3}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\end{array}$$

with log K=5.96. In order to control the coverage of a broad range of pH in the final equilibrium solutions, the system was titrated with either HCl (Acid) or NaOH (Base). The total initial amount of U and pH constitute hence the two degrees of freedom of the system, or inputs in ML-terms.

The targeted results of the geochemical simulations, included in the training dataset, are summarized in Table 1. They encompass: total aqueous uranium, U_aq​​​​​​​; total amount of sorbed uranium, U_s, itself consisting of the sum of exchanged, U_ex, and in surface complexes, U_sc; and the amount of precipitated metaschoepite. Amounts of Acid or Base needed to reach the prescribed pH are considered outputs as well; note that for uniformity of the original benchmark across the conventions of several geochemical simulators, a minimal value for either variable was set to 10⁻⁹ instead of 0.

Table 1 Output variables in the benchmark.

Further derived output variables are partition coefficients of uranium, expressed as Kd values, in terms of L kg⁻¹. Three different Kd are computed, with subscripts indicating the considered fraction: Kd_s for the ratio of U in the solid phase and in the aqueous phase; Kd_sc and Kd_ex for the U fractions in surface complexes and at exchange sites, respectively.

2.2 The training and validation datasets

The geochemical simulations introduced above have two free variables: total uranium and pH. For the purpose of the benchmark, uniform bivariate random samplings were drawn by latine hypercube in the logarithmic space pH × log ₁₀U, meaning that the samplings are uniform in the cartesian space $[\mathrm{2},\mathrm{12}]\times [-\mathrm{9},-\mathrm{2}]$ (cf. Table 2).

Table 2 Input parameters and ranges in the training dataset.

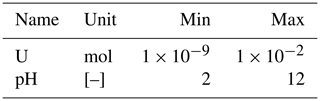
For a given random seed, samples of increasing length were generated: 5000, 20 000, 50 000 data points are used as training sets; validation datasets from a different seed comprising 20 000, 50 000 and 500 000 entries for validation. The coverage of the parameter space of the training dataset à 20 000 points is presented in Fig. 1. The colour-codes of the points in the figure will be explained in the next section.

Figure 1 Map of the uniform sampling in the coordinates pH and log ₁₀(U) for the 20 000 points dataset.

3 Methods

3.1 DecTree: Recursive partition of parameter space

The main idea of the DecTree approach is to exploit domain-specific knowledge for the training of the surrogate model. For the above introduced geochemical system, such a priori knowledge consists of:

1. either Acid or Base are larger than $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{9}}$

2. for the {pH, log ₁₀U} combinations where metaschoepite precipitates, the geochemical system honours its law of mass action, and thus they are fundamentally distinct from those where no precipitation occurs

3. known mass balance equation for uranium across sorbed, exchanged, metaschoepite, and aqueous phase.

The mass balance equation, written in terms of the variables included in the training dataset, reads:

$$\begin{array}{}\text{(1)}& \mathrm{U}=\mathrm{U}\mathrm{\_}\mathrm{aq}+\mathrm{U}\mathrm{\_}\mathrm{sc}+\mathrm{U}\mathrm{\_}\mathrm{ex}+\mathrm{Metaschoepite}\end{array}$$

It is easy to recognize that the first two facts of the a priori knowledge each define disjointed subsets within the training data. This can be clearly visualized in Fig. 1: the data points are coloured evaluating first the boolean condition “Acid > $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{9}}$” (or, equivalently, its complement), resulting in a non-linear binary partition. Secondly, in each of the two subregions, the second condition “metaschoepite > 0” (or its complement) is evaluated, resulting in a further binary split. The successive, hierarchical application of binary splits results in the four colour-codes of Fig. 1, much like a classical phase diagram separates fundamentally distinct regions based on thermodynamics.

The first learning task for the DecTree surrogate is hence to identify these regions, or equivalently their boundaries. This is in all effects a classical space partitioning problem. While many ML algorithms can solve it, a straightforward geometric approach was here preferred, based on the inexpensive computation of convex hull of a set of points. The convex hull is defined as the smallest closed convex polygon that encloses all the points in the set (Serra, 1982); assuming convexity ensures that the hull is unique and its computation very quick. Such a polygon is stored by DecTree as node of the tree, since it represents the boundaries of homogeneous regions identified from the data.

Note that the convexity of sets of points isn't guaranteed. DecTree addresses this issue by first computing convex hulls for both the region where a condition is true (such as mineral occurrence) and its complement. It then analyzes the confusion table of resulting in-sample classifications by means of point in polygon algorithm (Serra, 1982), which simply checks if a point lies inside a polygon or on the boundary, and is particularly efficient to compute in case of convex polygons. The absence of false positives for one hull is heuristically interpreted as evidence of that region's convexity, and is finally retained in the model. When neither subregion is convex, DecTree reverts to a more general but less precise concaveman parametric generalization (Park and Oh, 2012), followed by further morphological operations such as dilation of the hull (Serra, 1982), followed by the computation of the intersections between the dilated concave hull and its complement, in order to maximize the area covered by the hull while resolving possible overlaps.

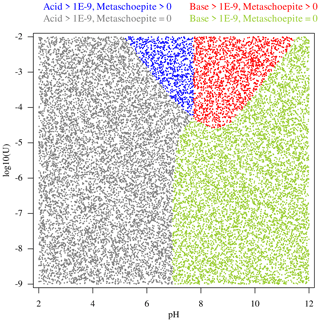
Figure 2 Matrix of scatterplots visualizing the dependencies between inputs (pH, log ₁₀U) and some of the outputs in a DecTree partition (Base > 1 × 10⁻⁹ and Metaschoepite > 0). Many perfect functional relationships appear, hence allowing for simplification or model reduction in the prediction step if identified correctly in the learning phase.

Once the hierarchy of space partitions in terms of region boundaries is learned, DecTree assesses the functional dependence among all possible input-output combinations in each of the resulting subset of training data. The importance of such exploratory step is illustrated in Fig. 2, which displays a matrix of scatterplots between all variables in a DecTree leaf. Very scattered point clouds imply no visible correlation; however in many instances a clear functional dependence appears (marked in red), which can be leveraged to simplify the prediction. The screening for functional dependence is performed via a heuristic extension of the Spearman rank-based correlation coefficient ρ, discussed in Sect. 3.2.

DecTree keeps track of the explained output variables in a leaf. The outputs identified as function of only one input are marked as “explained”, since they can be predicted by bivariate interpolation (cubic splines). The remaining outputs can be either predicted by the known mass balance equation, if all but one term in such equation are already explained; or, in the general case, they must be predicted by multivariate interpolation from all the inputs. In the current DecTree implementation, interpolation is performed via the highly efficient Multilevel B-spline Approximation (MBA) method (Lee et al., 1997; Hjelle, 2001). The application of MBA requires some heuristic setting such as the degree of the underlying B-splines and the ratio of the dimensions’ ranges.

The partition of training data after the hierarchical splits together with the indication of the required form of prediction for each output (bivariate, multivariate interpolation, or computation via mass balance) ultimately constitute the final leaf of a DecTree surrogate. The actual training data hence are retained as interpolation set (data from which interpolations are performed) in a DecTree model.

Note that all the aforementioned operations, convex hull, point-in-polygon check and MBA could be extended to higher dimensions than two, realistically up to dimension 5. This is however not yet explored at the moment, and proving this claim would require an implementation of these methods which is currently not available in the author's software environment.

3.2 Measures of functional association

In statistics and data science, a measure of dependence or statistical correlation between sets of points is a long-standing problem (e.g., Chatterjee, 2020). The well-known Pearson correlation coefficient only measures linear associations, while rank-based Spearman's ρ and Kendall's τ can deal with non-linear monotonic relationships. As a reminder, ρ is defined as the correlation coefficient between the ranks of two random variables:

$$\begin{array}{}\text{(2)}& \mathit{\rho }={\displaystyle \frac{\mathrm{cov}\left(\mathbf{R}\right(X),\mathbf{R}(Y\left)\right)}{{\mathit{\sigma }}_{\mathbf{R}\left(X\right)}{\mathit{\sigma }}_{\mathbf{R}\left(Y\right)}}}=\mathrm{1}-{\displaystyle \frac{\mathrm{6}\sum d_i^{\mathrm{2}}}{n(n^{\mathrm{2}}-\mathrm{1})}}\end{array}$$

where cov is the covariance operator, σ the standard deviation, R the rank operator and d the difference between the two ranks of the ith observation. By definition, $\mathit{\rho }\in [-\mathrm{1},\mathrm{1}]$ and it takes the extreme values if and only X and Y are in a perfect order relation. Kendall's τ (Kendall, 1938) and the successively introduced Hoeffding's D (Hoeffding, 1948) are rather statistical tests and as such they must be interpreted; while they capture general types of dependence, those do not again include non-monotonic relationships and do not guarantee to have a defined numerical value when the observations are in measurable functional dependence (Chatterjee, 2020).

Further measures have been devised in order to obtain reliable and fast association metric between variables in the general non-linear and non-monotonic case (Griessenberger et al., 2022, and references therein) both in presence of noise or not. Among them we can cite: Distance Correlation dCor (Székely et al., 2007), Maximal Information Coefficient MIC (Reshef et al., 2011), the copula-based quantification of asymmetric dependence qad (Junker et al., 2021) and Chatterjee's ξ (Chatterjee, 2020). All these methods are implemented in open source, freely available R extension packages and were tested for the purpose of this study in three different configurations (Fig. 3): (a) polynomial of degree 3 with added noise; (b) sinusoidal function; (c) non-function: different values of y are associated to the same x value.

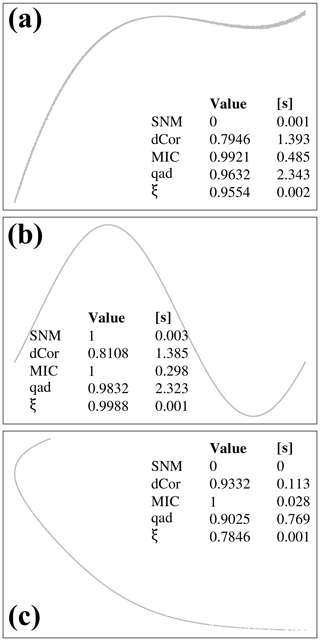
Figure 3 Comparison of different measures of bivariate association for variables with and without noise. SNM: Spearman Non-Monotonic (this work); dCor: Distance Correlation (Székely et al., 2007); ξ: Chatterjee measure (Chatterjee, 2020); qad: Quantification of Asymmetric Dependence (Junker et al., 2021); MIC: Maximal Information Coefficient (Reshef et al., 2011). (a) n=5000, polynomial of degree 3 with added gaussian noise; (b) n=5000, sin function; (c) n=1840, non-functional relationship between U_aq and U_sc from the uranium benchmark (partition Base > 1 × 10⁻⁹, metaschoepite > 0). The CPU time reported in seconds is rounded to the nearest third decimal digit.

However, none of these measures applied to the datasets from the considered benchmark were completely satisfying as a reliable measure of functional dependence. dCor and qad proved too computationally intensive for the purpose of this work; MIC, while being much faster, did not distinguish between perfect, non-noisy relationship and functional relationship, as it can be seen in Fig. 3c, which displays such kind of relationship. Chatterjee's ξ performed very well both in computational speed and in capturing the needed information; however, its computed final value in many cases only approaches unity for perfect functional association, hence requiring user decision to define a “threshold” above which a functional relationship could be reliably inferred.

Under the assumption of non-noisy relationship between the free variable x and the tested variable y, a straightforward semi-parametric extension of the Spearman coefficient for the non-monotonic case is possible. It relies on identification of local minima and maxima of the x,y function, a very inexpensive operation requiring only lagged differencing of order two of the y vector ordered for increasing x values. These extremants divide by definition the parameter space of the x,y relationship in monotonic intervals. For each interval i in which enough data points are present, the classical Spearman's ρ_i of Eq. (2) is then computed. Contiguous intervals in which $\left|{\mathit{\rho }}_i\right|=\mathrm{1}$ can then be joined to cover the region of parameter space in which a perfect functional association is recognized. For the purpose of this work, the computed values (SNM in Fig. 3, standing for Spearman Non-Monotonic) are the arithmetic mean of the absolute values of all the computed ρ_i. This extension is indeed only semi-parametric since the minimum number of points needed in a monotonic interval must be chosen – the value of 5 is used throughout this work. A naive implementation of SNM in the R language (Listing A1) is given in appendix. In particular, it is so implemented that even if just one interval holds not enough points, the function returns 0 instead of the average of the monotonic ρ_i. However, SNM guarantees to return 1 if and only if it is applied to perfectly functional relationships. The latter characteristic is not prioritized in the other metrics, which also do not guarantee to obtain 1 in case of perfect functional dependence (cf. ξ in case (b)), but capture “approximately functional” relationship.

As it can be seen in Fig. 3, SNM behaves as intended in all three cases, while being on par with ξ in computational speed even in the naive implementation of Listing A1, and can hence be relied on when inferring “physical behavior” from data. A further straightforward extension of the SNM would be to identify the sub-intervals in which the relationship between two variables is functional. This however is left for future work.

4 Results and discussion

As reminder, the benchmark described in Sect. 2.1 has two independent features, total U and pH, and comprises 10 distinct outputs, of which 6 are primary and the other 4 could be derived. However, all the outputs in the training dataset were directly predicted by DecTree in this exercise.

All input and output variables were log-transformed before the DecTree learning phase, with exception of pH (left untouched), and the amount of mineral metaschoepite, which was scaled by a factor of 1000. Note that if mass balance is used to predict an output, this has to consider back-transformed variables, while all bi- and trivariate interpolations are operated in the transformed parameter space, thus introducing a slight systematic bias in DecTree predictions. This also implies that the variables' preprocessing must be known by DecTree and hence constitutes one input to the routine.

The “physical knowledge” given to DecTree as input is: the disjointed occurrence of either Acid or Base; the fact that metaschoepite is pure mineral; and the mass balance Eq. (1). DecTree operates a first split of the {log₁₀U, pH} space based on the condition ${\log }_{\mathrm{10}}\mathrm{Acid}>-\mathrm{9}$. Since neither the region where the condition is true nor its complement are convex, the algorithm reverts to computing the concave hull. Each resulting subspace is further partitioned learning the region of metaschoepite occurrence, this time by convex hull. Within the four resulting subspaces, DecTree then correctly identifies functional dependencies between outputs and inputs. This is particularly evident in the leaves where metaschoepite occurs, where their number is elevated. Remaining variables are predicted by multivariate interpolation via the MBA method. The final form of the learned tree surrogate for this benchmark is displayed in Fig. 4.

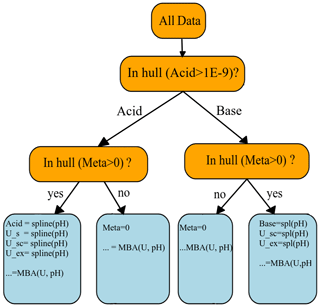
Figure 4 Output of the DecTree surrogate approach represented as a binary tree for the U-pH benchmark from the DONUT ML-benchmark initiative. The leaves of the surrogate indicate functional dependencies of outputs to the inputs: within each leaf, a mono- or bivariate interpolation of the training data returns the predictions. Spline stands for cubic splines, MBA for Multilevel B-spline Approximation bivariate interpolation. This tree is explainable by construction: it recognizes from the data that when the mineral metaschoepite occurs, the underlying system honours a “latent hidden constraint” which reduces its degrees of freedom. This results in a functional dependence of all or most output variables on a single input dimension in the corresponding regions.

Accuracy and performance. The current non-parallelized implementation of DecTree achieves excellent results in reproducing the validation data. In particular, DecTree is characterized by virtually no training time, competitive prediction throughput, and excellent accuracy. DecTree is able to produce results for all combinations of the three available dataset for training and four for validation in under 10 s using one single CPU core (Intel Xeon W-2133 CPU, up to 3.60 GHz).

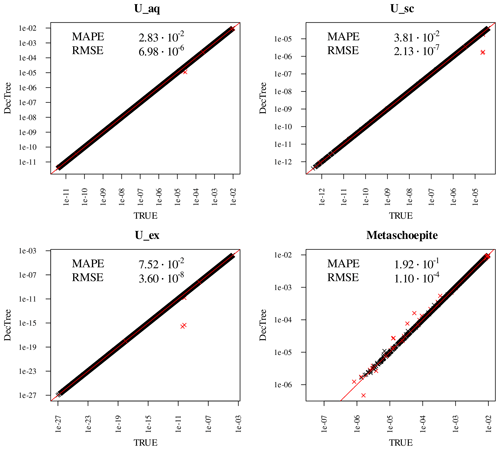
Figure 5 Scatterplot of selected DecTree predictions against validation dataset. All variables on logarithmic scale in both axes. Training data: 50 000 points; validation data: 20 000 points. From this figure it is visible how many variables span many orders of magnitude. Red points indicate predictions which incur in a mass balance error for uranium higher than 1 %. These points would be rejected in a coupled reactive transport simulator, but they are included in the displayed statistics.

Figure 5 showcases scatterplots between true and predicted outputs for four variables U_aq, U_sc, U_ex, and metaschoepite, obtained with a DecTree model trained on the 50 000 samples dataset and evaluated on the 20 000 validation set. All plots are in log-log scale to ensure capturing of discrepancies also at lower values. Two metrics are furthermore reported in each panel: the classical Root Mean Square Error (RMSE), and the relative (per observation) Mean Absolute Percentage Error (MAPE) which is capable to capture discrepancies at very low ranges:

$$\begin{array}{}\text{(3)}& \mathrm{MAPE}={\displaystyle \frac{\mathrm{100}}{N}}\sum \left|{\displaystyle \frac{y_i-\widehat{y_i}}{y_i}}\right|\end{array}$$

where N is the number of observations, y_i are the true values and $\widehat{y_i}$ the predicted. As such, the MAPE is defined only for strictly positive “true” y_i. Since however many of the variables have 0 as a physically meaningful parameter, in the cases in which y_i=0, the ratio in Eq. (3) is substituted by 0 if the predicted $\widehat{y_i}$ are zero, and 1 otherwise. More details and a more in-depth discussion of the metric choice can be found in Prasianakis et al. (2024a). The advantage of the thus defined MAPE is that it can be read as a percentage: MAPE = 2.2 × 10⁻² means 0.022 % relative error. This makes also MAPEs comparable between different variables, which is not possible with the standard RMSE.

Note that no variable was predicted by mass balance in the tree of Fig. 4. This allows to check plausibility of predictions, evaluating the lost mass of U in the outputs. In Fig. 5 the points exceeding 1 % error of the initial total U are plotted in red: this criterion captures most of the outliers in those variables. The reported metrics include those outliers, while of course in view of application to coupled reactive transport simulations, those points would be rejected.

The single main factor controlling the accuracy of the surrogate predictions is in any case the hierarchical partitioning based on geometry. The misclassification of validation points is limited (i.e., 14 points in the 20 000 validation set when DecTree is trained on the 50 000 training dataset, cf. Fig. 5).

The MBA approximator suffers from some over- and undershooting near the borders of the interpolation domain, but only a minimal amount of validation points are actually affected by this problem. Again, refusing to predict points near the region boundaries would easily improve the accuracy of the surrogate predictions in a coupled RTM scenario, delegating the “full physics” geochemical simulation. It is intuitive that such an approach profits greatly from refined sampling near the “physical boundaries” or transition regions in the parameter space, since DecTree relies on geometric computations to learn them. Conversely, within each region, the data could actually be downsampled far from those boundaries without incurring significant loss of accuracy, given the smoothness of the response surfaces. Since in general the prediction speed depends quadratically on the amount of points used for interpolation, less retained points would further increase the throughput of DecTree.

Table 3 Training and prediction time for the DecTree surrogate for the different training and validation datasets. Throughput is inversely proportional to the number of data retained for interpolation. MAPE(Meta) stands for Mean Absolute Percentage Error for mineral metaschoepite.​​​​​​​

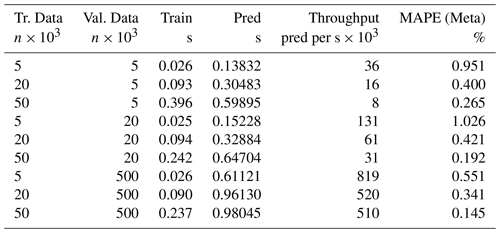
Table 3 reports training and prediction timing on 1 single core. The training time is completely negligible, 50 000 data points are processed in about 0.24 s. The throughput of the prediction is however heavily impacted by the amount of data retained in the interpolation set. This is because the data are irregularly sampled, and each interpolation must setup a data structure and perform a search for neighbouring points once, at initialisation. Still, the prediction is very fast, achieving around 500 000 predictions per second when trained on the 50 000 dataset.

For comparison, the numerical simulator used to compute the training and validation datasets has a throughput of around 40 000 simulations per second on a single core on the same desktop machine used to evaluate the DecTree performance as in Table 3. More details about the the efficiency of different methods and of geochemical simulators can be found in Prasianakis et al. (2024a).

The here described single-core implementation of DecTree could be further improved by parallelization, in particular to increase the prediction throughput. In the learning phase, parallelization can be employed in the screening for functional dependence within each partition. In the prediction phase, a linear increase in prediction throughput can be expected, provided enough requests are there to make up for the overhead.

The interpolation from scattered 2D data is the bottleneck during prediction: this part could theoretically profit from a GPU (Graphic Processing Unit) implementation. However there are more fundamental improvements in the algorithm still needed before looking into these technical implementation details, especially the ability to deal with more complex systems and higher dimensionalities.

5 Conclusions and future work

The physics-based DecTree approach demonstrates promising results when applied to low-dimensional geochemical benchmark related to sorption of U(VI) on clay. With respect to the original DecTree version (De Lucia and Kühn, 2021), this application considers datasets which uniformly cover the range of input variables. The principles of operating a non-linear recursive parameter space partitioning were implemented via geometric algorithms. The same principles can be leveraged to substantially reduce the required training time for many black-box AI/ML surrogates, such as Gaussian processes and artificial neural networks. Further research is required to extend its applicability to more complex systems, beginning with mechanisms to embed domain knowledge for chemical processes other than sorption and precipitation or dissolution of pure mineral phases. This concerns both the implementation and the actual construction of the method itself. In particular, the current implementation cannot deal with nested or disjointed mineral occurrences. This prevented its application to other benchmarks from the DONUT project, such as those for the cementitious systems (Prasianakis et al., 2024a).

The DecTree approach achieves its high accuracy by interpolating new predictions directly from the training data and by reducing the dimensionality of interpolation for variables for which functional dependence is identified. To this end, a straightforward extension of the Spearman's rank coefficient has been devised for non-monotonic relationships.

Approximators such as MBA and the algorithms of computational geometry such as convex hull and point-in-polygon are well defined in higher dimensions, but their actual efficiency remains to be assessed in higher dimensionalities.

Appendix A: Computing the non-monotonic Spearman coefficient

Listing A1 R code implementing Spearman's ρ (function Spear) and the non-monotonic extension SpearmanNonMonotonic adopted in this study. Note that this implementation does not deal with missing values in either of the two variables for which functional dependence is checked.