Combination of precise orbit solutions for Sentinel-3A using Variance Component Estimation
Cyril Kobel
Daniel Arnold
Adrian Jäggi
In this article we analyze the benefit of computing a combined solution from individual orbit solutions for the low Earth orbiting satellite Sentinel-3A. The selected combination scheme for calculating the combined solution is Variance Component Estimation (VCE). Before a combination is calculated, the individual orbit solutions are analyzed to identify systematic differences and characteristics. Simulation studies are performed to show under which conditions a combined solution of superior quality may be expected. The combined solution is validated by Satellite Laser Ranging (SLR) measurements and compared with SLR validations of the individual solutions. The result of this investigation shows that VCE, implemented as an iterative procedure, is suitable to obtain an orbit solution of superior quality for Sentinel-3A.
- Article
(1312 KB) - Full-text XML
- BibTeX
- EndNote
Precise Orbit Determination (POD) of Low Earth Orbiters (LEO) plays an important role for studies in various fields. Global Positioning System (GPS) data together with precise GPS satellite orbits and satellite clock corrections provided by the International GNSS Service (IGS, Johnston et al., 2017), data from the French DORIS (Doppler Orbitography and Radiopositioning Integrated by Satellite) system or from Satellite Laser Ranging (SLR) are used to perform LEO precise orbit determinations. To determine a precise orbit, a physical model of the orbit is fitted to the corresponding tracking data. The combination of force models and precise tracking data, the so-called reduced-dynamic approach, provides the framework to fulfil the precise orbit requirements in terms of precision and computation time (Wu et al., 1991).
Nowadays for many LEO satellites with stringent accuracy requirements, the precise orbits are calculated on an operational basis. In addition several POD expert centers are also providing solutions in off-line processings. Since the calculated reduced-dynamic orbits are based on a physical force model, different orbits can result if different background models or different orbit parametrizations are used. The software used for the corresponding calculations can also lead to differences.
The existence of different solutions for one and the same orbit raises the question if there is a solution that represents the orbit better than all others do. Furthermore, the question arises whether a combination of such different solutions can lead to an orbit of superior quality.
In this article this question is investigated by using the precise orbit solutions of the satellite Sentinel-3A. Sentinel-3A forms together with Sentinel-3B a pair of Earth observation satellites which are part of the Copernicus, or formerly GMES (Global Monitoring for Environment and Security) program (Aschbacher and Milagro-Pérez, 2012). The European Copernicus Program provides Earth observation data for environmental protection, climate monitoring, natural catastrophes assessment and other societal purposes.
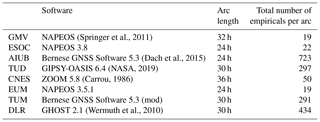
Sentinel-3A was launched on 16 February 2016, from the space port Plessezk with a Rockot sky rocket into a sun-synchronous orbit at an altitude of about 800 km. The specific task of Sentinel-3A is ocean observation. It is equipped with corresponding instruments for this purpose. Besides those, it is also equipped with two GPS receivers to allow for POD (Montenbruck et al., 2018) with the goal of 2 cm RMS residual orbit accuracy (Fernández et al., 2016). As part of the so-called Sentinel POD Quality working group (QWG), different Analysis centers (ACs) are routinely computing orbit solutions for Sentinel-3A. From the list of ACs that provide these solutions, eight institutions have been selected for which the solutions will be analyzed in more detail and eventually used to generate a combined solution:
-
GMV (Grupo Mecánica del Vuelo, CPOD solution)
-
AIUB (Astronomical Institute, University of Bern)
-
TUM (Technical University of Munich)
-
CNES (Centre National d'Etudes Spatiales)
-
TUD (Delft University of Technology)
-
EUM (European Organisation for the Exploitation of Meteorological Satellites)
-
DLR (German Aerospace Center)
-
ESOC (European Space Operations Center of ESA)
These institutions regularly provide independent orbit solutions for the Sentinel-3 satellites. They are produced with different software packages and are based on different reduced-dynamic orbit determination approaches. The orbit solutions used in this study are based on GPS data only, while other ACs of the QWG also use DORIS for the POD (GMV, 2018a). SLR data may be used for an independent validation of the orbits for the Sentinel-3 satellites. Sentinel-3A was selected for this study because within the QWG many different solutions are provided by the ACs. In addition, Sentinel-3A has the highest accuracy requirements of the Sentinel satellites and features a Laser Retro Reflector, which makes SLR validation possible.
(Springer et al., 2011)(Dach et al., 2015)(NASA, 2019)(Carrou, 1986)(Wermuth et al., 2010)Table 1 shows that the parametrizations, especially the total number of empirical parameters per arc differs very much when comparing the solutions of the different ACs. In general it can be stated that the larger the number of empirical parameters the less dynamic is the corresponding orbit determination approach. Those parametrization differences can reveal biases, e.g. in radial direction, when comparing the different orbit solutions against each other (Peter et al., 2017).
The article is structured as follows. In Sect. 2 we will introduce the framework of Variance Component Estimation (VCE) used to compute combined orbit solutions as a weighted average of the individual orbit solutions from the QWG. In Sect. 3 a comparison between the different solutions is carried out. Section 4 deals with simulations, made to examine the impact of different types of orbit errors when using VCE. The application of VCE to real orbit solutions of Sentinel-3A is shown in Sect. 5. In Sect. 6 the combined solutions as well as the individual solutions are validated using SLR measurements.
The method used for the combination is based on VCE. The formulas can be derived from the results presented in Kusche (2003) and Teunissen and Amiri-Simkooei (2008). The combined solution is computed as a weighted average of the individual solutions. The weights of the individual solutions are a priori unknown and determined using VCE. The positions of the combined solution are determined independently for each epoch in this study. The corresponding set of weights is iteratively determined using daily batches of the individual orbit solutions. Note that in the adopted procedure correlations between components of the position vector and positions referring to different epochs are neglected.
The combination is represented, under the above mentioned simplifications, by the following formulas (Jean et al., 2018):
In each iteration new weights are thus calculated for each of the individual solutions. The computation is based on the weights of the previous iteration and the RMS of the difference of the individual solution to the combined solution of the previous iteration. xk represent the individual orbit solutions in the earth-fixed frame. Since the orbital solutions of the individual ACs are given in 3-D space, xk can be either interpreted as a one dimensional quantity or as a full position vector. This results in two possible strategies for the combination. It would be possible to compute the combination for each of the spatial directions xk∈ () independently of the others. With this variant, one RMS would be determined per spatial direction, per iteration and per solution. In the other variant, the differences of all spatial directions are used together and a single RMS is determined per individual solution per iteration. Various tests have shown that generally the version with one weight per solution is better suited. In addition, the separation of the three spatial directions of a solution is questionable, because they are not independent of each other. Therefore for each individual solution one weight per day is iteratively determined. The sampling for the combined solutions is 60 s. If the procedure is aborted after one iteration (i=1), the procedure is similar to the original method used for the combination of GNSS satellite orbits from different ACs as implemented by the IGS (Beutler et al., 1995).
Helmert transformations between individual solutions may be applied prior to the combination in order to reduce systematic differences between the individual solutions. For this purpose one solution is selected as a reference solution and all other solutions are transformed to the frame of the reference solution. Systematic differences such as offsets, rotations and scale differences can thus be eliminated if necessary. They will be reflected in the corresponding Helmert parameters. The Helmert transformation matches one set of orbit positions with another set of orbit positions according to
where Xi, Yi and Zi are the original coordinates and , and are the transformed coordinates. The Helmert parameters are a displacement vector with three components (), a scale factor (1+μ) and a rotation matrix consisting of three (small) rotation angles () around the coordinate axes. These parameters are iteratively determined using the classical non-linear least-squares adjustment (Watson, 2006).
Before a combination of the individual solutions is computed, the solutions are mutually compared to each other. This serves the purpose to quantify and characterize potential systematic differences between the individual orbit solutions. In addition, such comparisons serve to identify degraded solutions and to exclude them from the combination if necessary. As such comparisons are regularly carried out and published by GMV in the frame of the regular Copernicus POD Service reviews (GMV, 2018b), the comparisons also serve the purpose of verifying our results. The comparison was performed for the period from 1 January 2017 to 27 January 2018.
Table 2Orbit comparison in the local orbital frame, CPOD vs. other solutions, no Helmert transformation applied, average of daily values.
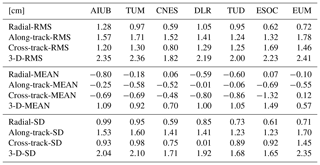
Since one may lose track from a cross-comparison between all solutions, a reference solution is selected and the differences between this solution and all others are calculated. The orbit differences, which are given first in the earth-fixed reference frame used by the sp3 orbit exchange file format (Remondi, 1993), are transferred to the local orbital frame defined by the radial, along-track, and cross-track direction. The first comparison is shown in Table 2. No Helmert transformation was applied and the official Copernicus POD (CPOD) service solution was used as a reference. Table 2 shows that different solutions may have systematic differences, e.g. systematic radial biases as already discussed by Peter et al. (2017) for Sentinel-1. It can also be seen that the radial mean value between some solutions is small, e.g. between the GMV and the ESOC orbit solutions. This is also the case when comparing the GMV to the EUM orbit solution. This reflects the use of the same software (NAPEOS) and similar orbit parametrizations by these three ACs. A small mean value also shows up in the radial direction in the comparison of GMV and CNES orbit solutions. According to GMV (2018a) both ACs do not make use of empirical parameters in radial direction and use a similar number of total empirical parameters per arc (see Table 1) resulting in a rather dynamic orbit representation. The combination of small differences and not setting up empirical parameters in radial direction are an indicator of very similar modelling of the radial direction by these ACs. A larger systematic difference, e.g. in radial direction between the GMV orbit solution and the AIUB orbit solution, reflects the large difference in total number of empirical parameters (see Table 1). This shows that GMV's orbit determination approach yields orbits of more dynamical stiffness than the AIUB orbit determination approach, which may be exploited to detect inconsistencies in the adopted antenna phase center offset (PCO) corrections or center-of-mass coordinates (Peter et al., 2017). It can be stated here that the ACs are essentially divided into two groups, one group performing a very dynamic orbit determination approach, and the other one with relatively large total number of empirical parameters, a more reduced-dynamic one.
Table 3Orbit comparison in the local orbital frame, CPOD vs. other solutions, average of daily values.
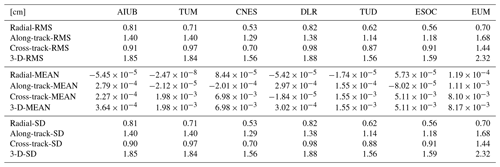
In addition to the SD, which indicates the variability between orbit solutions, the RMS is calculated as well, because this value also includes systematic offsets. The RMS is therefore well suited to quantify the total differences between different solutions. In order to reduce systematic differences, a Helmert transformation is carried out before the comparison, i.e. before computing the orbit differences, where again the CPOD solution serves as reference, both for the transformation and for the comparison. In Table 3 the very small mean values are clearly visible, because the Helmert transformation reduces by construction systematic biases, rotations and scale differences. In addition, both SD and RMS became smaller in all comparisons.
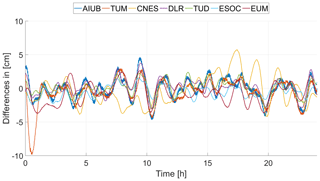
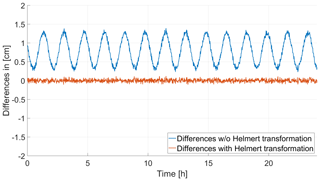
Figure 1Along-track differences between individual solutions and CPOD solution for 24 September 2017, no Helmert transformation applied.
In order to characterize the different types of differences, the residuals of an example day are plotted in Fig. 1 in along-track direction. The CPOD solution serves again as reference. One can clearly see that the differences are not random but approximately once-per-revolution periodic.
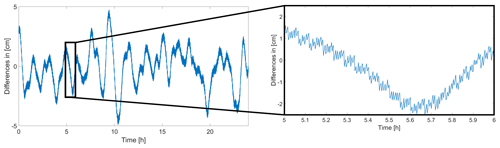
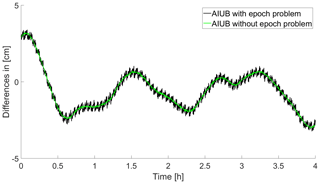
Figure 2Epoch problem revealed by the comparison of AIUB versus CPOD solution in the along-track direction.
Figures 1 and 2 furthermore reveal that differences involving orbit solutions computed with the Bernese GNSS Software (Dach et al., 2015) show a high-frequency noise in the along-track direction. This effect is a pure artefact of the Bernese GNSS solutions (AIUB, TUM). If these solutions are included in the combination, this problem will smear on the combination.
The problem is related to the use of the Modified Julian Date (MJD) as time argument when accessing the positions of the numerically integrated reduced-dynamic orbits in the Bernese GNSS Software. It can be easily cured when orbit positions are requested at integer seconds as it is the case for Sentinel-3A (see Fig. 3).
The example of the outlined epoch problem of orbit solutions computed with the Bernese GNSS Software underlines that a rigorous examination of the individual solutions needs to be performed first and potential issues should be sorted out before computing a combined solution. Otherwise artefacts of an individual solution will propagate into the combined solution.
In this section we investigate the reduction of different error types in the combination.
4.1 Random errors
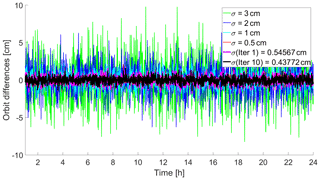
First we assess the benefits of VCE when combining orbit solutions affected by different levels of white noise. For this purpose four solutions are simulated, where the true orbit is assumed to be zero for the sake of simplicity. To each of the solutions we add white noise with an expectation value of zero and a specific standard deviation of 0.5, 1, 2 and 3 cm, respectively. The four solutions are then combined with VCE. In order to asses the quality of the combined solution, we examine the differences with respect to the true solution and compute its standard deviation. In addition, the results after the first iteration and after the tenth iteration are compared. Figure 4 shows the different time series over 24 h.
Figure 4 shows that the combination with VCE works perfectly well in this scenario as to be expected. It is noteworthy that after one iteration the standard deviation of the combined solution may be still larger than that of one specific single solution due to the different noise levels of the individual solutions. After several iterations, however, the combined solution outperforms all individual solutions when adopting VCE.
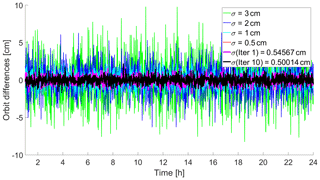
Nowadays, the IGS routinely calculates a combined solution for the orbits of GNSS satellites. The original combination method differs from the one used in this study in determining the weights according to . A comparison of the two combination strategies is shown in Figs. 4 and 5. It can be seen that if the weighting corresponds to that originally used by the IGS, the combined solution will converge to the best of the individual solutions but not to a superior solution. Only when adopting the VCE scheme, the combined solution converges towards a solution of superior quality. Note that both schemes are equivalent if the combination is truncated after the first iteration.
4.2 Systematic errors
In Sect. 3 it was shown that real orbit solutions are affected by systematic, in particular by periodic differences. In order to investigate the behaviour of VCE when combining solutions affected by systematic, periodic errors, additional simulations are carried out. For this purpose orbit solutions are simulated which are characterized by once-per-rev periodic errors with different amplitudes and phases. The errors are simulated according to
where ω denotes the angular frequency of the orbital period of about 90 min for a LEO satellite, Ai the specific amplitudes of the simulated errors and ϕi their phases. The individual solutions affected by the periodic errors from Eq. (3) are then combined using VCE as shown in Fig. 6.
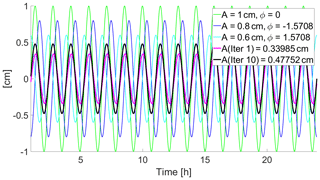
Figure 6Simulation of orbital errors with different amplitudes and phase shifts and their impact on the variance component estimation.
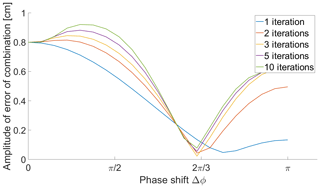
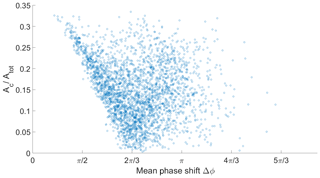
Figure 7Resulting amplitude of error of combined solution with different phase shifts when using three individual solutions for the combination.
In order to investigate the impact of phase differences to the quality of a combined solution, three individual solutions were simulated with a periodic error of identical amplitudes. Two of the three phases were constructed with the same difference to the third phase (once positive and once negative). Figure 7 shows the amplitude of the combined solution as a function of the phase difference. The error of the resulting combination with respect to the true solution is plotted as a function of the mutual phase difference (Δϕ) between the simulated periodic errors. A minimum is clearly visible. The exact position of the minimum depends on the amplitudes of the simulated errors of the individual solutions. In general, the simulation shows that the larger the phase shifts between the individual solutions, the smaller the amplitude of the error of the combined solution. The result for three individual solutions shown in Fig. 7 can be generalized to any number of solutions (not shown). The minimum approximately occurs at , where n denotes the number of solutions.
In further simulations, three individual solutions were generated with both their relative phases and amplitudes being chosen randomly. Based on this the ratio between the amplitude of the error of the combined solution (Ac) and the square root of the sum of the amplitudes squared of the errors (Atot) of the individual solutions is determined. Figure 8 shows this ratio (Ac∕Atot) as a function of the mean phase difference. The same pattern as in Fig. 7 can also be seen here, which allows to draw two conclusions. On the one hand, the amplitude of the error of the combined solution is always smaller than the square root of the sum of the amplitudes squared of the errors of the individual solutions. On the other hand, Fig. 8 shows that for increasing the mean value of the phase differences, the probability of an additional improvement for the combined solution increases as well.
From the results of the simulations it can be concluded that VCE will still be able to reduce the errors observed in real orbits even though they are not random but periodic. In order to generate combined solutions from real data, which ultimatively shall be of better quality than the individual solutions, periodic orbit errors need to fulfil the above mentioned criterion regarding the phase shifts.
To further investigate this, the phases of the differences of individual real orbit solutions are determined by Fourier analysis. This analysis confirms that all solutions have indeed different phases with non-zero mean (not shown). However, the exact mean value of the phase differences varies greatly from day to day. From this result and from the simulation it can be concluded that VCE will be able to reduce the periodic errors observed in real orbit solutions.
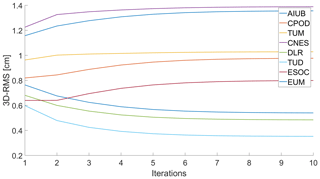
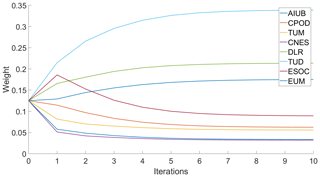
Since VCE is an iterative procedure, we have to determine how many iterations are necessary until convergence is reached. To determine this number, real Sentinel-3A orbit solutions from the QWG were combined with VCE. The RMS of the individual solutions to the previous combination was determined in each iteration, according to Eq. (1). Figure 9 shows the values as a function of the number of iterations for the example day 24 September 2017. It was found that the combined solution changes only marginally after eight iterations. Figure 10 shows the corresponding weights with increasing number of iterations for this example day. In Fig. 9 it can be seen that the RMS stabilized after several iterations. The same can be seen in Fig. 10 for the weights. We therefore set the number of iterations to ten for the combined solutions.
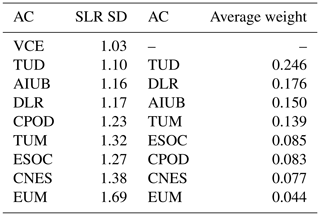
VCE is applied to the individual solutions of the period from 1 January 2017 to 27 January 2018. In this time series each individual solution receives one weight per day. The mean values of the weights for the analyzed time series are given in Table 4. No Helmert transformation was applied for this test. Table 4 shows that TUD gets the highest weight on average. It is of interest if the solutions with the highest weights on average are also the ones which represent the most accurate orbits. This will be addressed by validating the orbit quality of all solutions with independent SLR data (see Sect. 6).
In total ten different combinations are calculated for each day of the analyzed time period. Two combinations were computed without Helmert transformation; one aborted after one iteration and the other one aborted after ten iterations. The other eight combinations are each performed with a previous Helmert transformation, where one of the eight solutions served as the reference solution to which the other solutions were transformed by a Helmert transformation. Those combinations were also aborted after ten iterations.
Some ACs do not provide solutions for manoeuvre days. In addition, it may be possible for other reasons that an individual solution is not provided for some days. For the combination, a solution was determined using the solutions existing of the respective days. The amount of non-existent data over the period examined is only 2.3 %. Due to this small percentage, it is assumed that the neglect of these missing days for the statistics of both the comparison and the SLR validation is irrelevant.
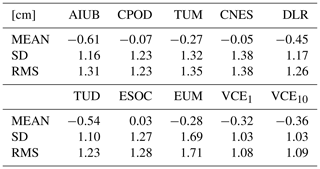
Sentinel-3A is equipped with a Laser Retro Reflector (LRR) which allows SLR tracking of the satellite by the station network of the International Laser Ranging Service (ILRS, Pearlman et al., 2002). Since all individual solutions are calculated with the same set of GPS observations, an independent technique like SLR is required for orbit validation. This guarantees that the solutions are not prone to biases that affect all individual solutions in the same way, e.g., in the radial direction, which would not be noticed in a cross-comparison (GMV, 2018b). SLR is primarily, although not exclusively, sensitive to the radial direction. Additionally, in order to independently validate if VCE, especially as an iterative method, is advantageous for the combination of different LEO orbit solutions, SLR measurements can be used. SLR residuals are therefore computed for the combined solutions as well as for the individual orbit solutions of each AC. The SLR validation was performed using the Bernese GNSS Software. The validation was performed for the entire time period from 1 January 2017 to 27 January 2018. For the validation of the SLR measurements, only observations from a subset of well performing stations were used: The list of accepted stations was compiled on the basis to externally determined quality of the measurements (GMV, 2018b, Table 5). A threshold of 20 cm was set for the residual outlier detection. Table 6 shows the statistics of the SLR validation. The number of accepted measurements per day are mostly between 50 and 250. It is worth mentioning that the number of rejected observations for most days is zero. For days on which manoeuvres took place no validation is performed. The combined solutions (VCE) shown in Table 6 were determined without a previous Helmert transformation. The subscript denotes the number of iterations for the combined solutions.
Table 5SLR stations from which the observations were used with corresponding number of accepted observations for the investigated time period.
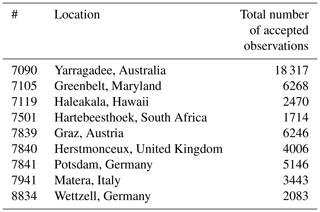
Table 6 shows that the standard deviation (SD) of the combination is smaller than the SD of any of the individual solutions. This underlies the superior quality of the combined solution. It is also noteworthy that the mean value of the combined solution is, however, not the smallest, but rather represents a weighted average of the mean values of the individual solutions. However, one has to keep in mind that, due to potential inconsistencies in the satellite geometry, the best orbit solution might not show the smallest mean value for the SLR residuals. To avoid mixing the levelling of individual solutions in the combined solution, a Helmert transformation of the individual solutions w.r.t. one reference solution can be performed prior to the combination. It is also evident that the mean value and the RMS assume larger values as the number of iterations increases, but not the SD.
Table 7 presents the SLR validation with one solution serving as a reference when adopting a Helmert transformation prior to the combination. If no solution was calculated for such a reference solution for a specific day, no combined solution was determined.
Table 7SLR validation of combined orbit solutions by using variance component estimation with previous Helmert transformation.

It is noteworthy that the standard deviation only becomes smaller than in Table 6 for the combination where DLR is chosen as a reference orbit. In all other combinations, the standard deviation is larger than when no Helmert transformation is applied but smaller than the standard deviation of the corresponding (reference) individual solutions.
Why the DLR orbit solutions used as reference for a prior Helmert transformation leads to the best combined orbit solution, in terms of SD of SLR residuals, can not be answered conclusively. One possibility could be that the number of empirical parameters in the computation of this solutions is a good compromise between dynamic and reduced-dynamic orbit determination approach. In Table 4, however, it can be seen that the combination scheme (VCE) gives a high weight to the DLR solution on average. Also the combined solution with TUD as reference, which receives the highest weight in average, shows a comparatively small SD of the SLR residuals. The reason for this high weight is the good agreement of the TUD solution to all the other solutions in cross-comparisons (not shown). If therefore a combined orbit solution is to be computed, a reference solution should be selected from which it is known that it has a small mean value in the SLR residuals and then a combined solution with previous Helmert transformation should be carried out using VCE to further improve the SD. If no such reference solution is known, no Helmert transformation should be carried out before performing a combination. Additionally the orbit solution which gets the highest weight in this combination procedure (without prior Helmert tranformation) can be used as reference for a Helmert transformation for another combined solution, to further improve both the mean and SD of the SLR residuals. If it is known that one of the solutions is significantly worse than the other solutions, e.g. by a translation, it should be included anyway, since when not carrying out a prior Helmert transformation, the combination scheme will strongly decrease the weight of this solution. If a prior Helmert transformation is carried out in this scenario the translation will be compensated and the initially worse solution can contribute to the combined solution.
Table 8SLR validation of combined orbit computed by GMV (COMB) and combined solution using variance component estimation (VCE10).
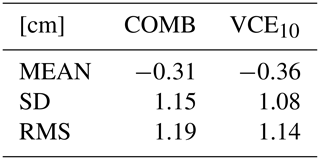
GMV is also operationally computing a combined orbit solution (COMB) from the orbit solutions of the individual ACs, but in this combination the weights are determined according to . This combination is computed with a prior Helmert transformation. The SLR validation in Table 8 shows that the combination computed using VCE has a smaller standard deviation and a slightly larger mean value than the combination computed by GMV. Direct orbit comparisons of the combined solution computed by GMV and the combined solution computed using the presented combination method reveal a 3-D RMS of 0.49 cm for the time period from 27 January to 18 May 2019.
In order to illustrate that the weights assigned by the VCE algorithm generally nicely correspond to the actual orbit quality, we show the average weights, after the 10th iteration of the combination procedure without prior Helmert transformation, together with the average SD of the SLR validation in Table 9. Since the values in both the columns are determined completely independent of each other, the coincidence of the order of the ACs is a very strong indication that using VCE as combination scheme is advantageous for computing combined orbit solutions for Sentinel-3A.
Varieties between different combined solutions, obtained by using different reference solutions, are analyzed. The differences in such comparisons look similar to differences in comparisons between individual solutions unless a Helmert transformation is performed beforehand. When performing a Helmert transformation before the comparison, the differences of combined solutions vanish to a large extent, see Fig. 11. This implies that the combined solutions with previous Helmert transformation differ mainly by a rotation, scaling and translation.
The method of variance component estimation can be successfully applied to the combination of precise orbit solutions of the Sentinel-3A satellite computed in the frame of the POD Quality Working Group. It could be shown that the SD of the SLR measurements is further improved by the combination process, which is a good indicator for the superior quality of the combined solution. However, the mean value of SLR residuals is worse than for some of the individual solutions when not applying a Helmert transformation. An attempt was made to eliminate systematic differences before the combination by making use of a Helmert transformation before performing the combination with VCE. It turned out that the combination by VCE in this case shows a smaller SD of the SLR residuals than the individual solutions used as reference. Both the simulation of the periodicities and the values of the SLR validation for the mean value and RMS show that more than one iteration can also be disadvantageous in the presence of systematic errors. By performing a Helmert transformation before the computation of the combination it is possible to reduce the mean value to a large extent if a solution is chosen as reference which has a small mean value in the SLR validation itself. Since the simulations with solutions affected by white noise showed that a increasing number of iterations is advantageous and due to the fact that by performing a previous Helmert transformation the mean value of the SLR residuals can be controlled, it can be stated that making more than one iteration is advantageous and should therefore be done to get an orbit of superior quality. The magnitude of the improvement of the combined solution over the individual solutions is at least 6.4 %, which is considered as relevant.
The order of the ACs in terms of SLR SD and weights given by VCE is very similar. One can see that the ACs which receive on average the highest weights are also the ones with the smallest standard deviations in the SLR validation. It is encouraging to see that the weights reflect the SLR validation. From this it can be concluded that the combined solution converges to a superior solution in most cases. In our opinion the findings are well transferable to other satellite missions.
Further improvements of the combination method are conceivable, e.g. with regard to the correlated spatial directions and correlations in time.
The data is not publicy accessible. The different individual orbit solutions are computed in the frame of the Quality Working Group and are only available for members of the QWG. To access the data, please contact the authors.
CK designed the study, planned and carried out the simulations, performed the computational framework and analyzed the data. DA contributed to the SLR validation. AJ developed the theoretical formalism and contributed to the discussions. All authors discussed the results and contributed to the final manuscript.
The authors declare that they have no conflict of interest.
This article is part of the special issue “European Geosciences Union General Assembly 2019, EGU Geodesy Division Sessions G1.1, G2.4, G2.6, G3.1, G4.4, and G5.2”. It is a result of the EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019.
Helpful discussions about the combined solution by GMV with Heike Peter and Jaime Fernández Sánchez are kindly acknowledged. Additional thanks to the Copernicus POD QWG for providing the individual solutions, which made it possible to do this study. Kindly acknowledged is also the careful reading of the manuscript including adding useful comments by the reviewers.
This paper was edited by Sigrid Böhm and reviewed by two anonymous referees.
Aschbacher, J. and Milagro-Pérez, M. P.: The European Earth monitoring (GMES) programme: Status and perspectives, Remote Sens. Environ., 120, 3–8, https://doi.org/10.1016/j.rse.2011.08.028, 2012. a
Beutler, G., Kouba, J., and Springer, T.: Combining the orbits of the IGS Analysis Centers, B. Geod., 69, 200–222, https://doi.org/10.1007/BF00806733, 1995. a
Carrou, J. P.: Zoom Software: Error Analysis and Accurate Orbit Restitution at CNES, in: Space Dynamics and Celestial Mechanics, edited by: Bhatnagar, K. B., 381–398, Springer Netherlands, Dordrecht, 1986. a
Dach, R., Andritsch, F., Arnold, D., Bertone, S., Fridez, P., Jäggi, A., Jean, Y., Maier, A., Mervart, L., Meyer, U., Orliac, E., Ortiz-Geist, E., Prange, L., Scaramuzza, S., Schaer, S., Sidorov, D., Susnik, A., Villiger, A., Walser, P., and Thaller, D.: Bernese GNSS Software Version 5.2, https://doi.org/10.7892/boris.72297, University of Bern, Bern Open Publishing, Bern, 2015. a, b
Fernández, J., Fernández, C., Féménias, P., and Peter, H.: The Copernicus Sentinel-3 mission, in: ILRS workshop, 1–4, 2016. a
GMV: Regular Service Review, October 2017 to January 2018 GMV, available at: https://sentinel.esa.int/web/sentinel/missions/sentinel-3/ground-segment/pod/documentation (last access: 23 May 2019), 2018a. a, b, c
GMV: SLR Yearly Report GMV, available at: https://sentinel.esa.int/web/sentinel/missions/sentinel-3/ground-segment/pod/documentation (last access: 23 May 2019), 2018b. a, b, c
Jean, Y., Meyer, U., and Jäggi, A.: Combination of GRACE monthly gravity field solutions from different processing strategies, J. Geodesy, 92, 1313–1328, https://doi.org/10.1007/s00190-018-1123-5, 2018. a
Johnston, G., Riddell, A., and Hausler, G.: The International GNSS Service, 967–982, Springer International Publishing, Cham, https://doi.org/10.1007/978-3-319-42928-1_33, 2017. a
Kusche, J.: A Monte-Carlo technique for weight estimation in satellite geodesy, J. Geodesy, 76, 641–652, 2003. a
Montenbruck, O., Hackel, S., and Jäggi, A.: Precise orbit determination of the Sentinel-3A altimetry satellite using ambiguity-fixed GPS carrier phase observations, J. Geodesy, 92, 711–726, https://doi.org/10.1007/s00190-017-1090-2, 2018. a
NASA: GIPSY-OASIS Jet Propulsion Laboratory, available at: https://gipsy-oasis.jpl.nasa.gov, last access: 30 August 2019. a
Pearlman, M., Degnan, J., and Bosworth, J.: The International Laser Ranging Service, Adv. Space Res., 30, 135–143, https://doi.org/10.1016/S0273-1177(02)00277-6, 2002. a
Peter, H., Jäggi, A., Fernández, J., Escobar, D., Ayuga, F., Arnold, D., Wermuth, M., Hackel, S., Otten, M., Simons, W., Visser, P., Hugentobler, U., and Féménias, P.: Sentinel-1A – First precise orbit determination results, Adv. Space Res., 60, 879–892, https://doi.org/10.1016/j.asr.2017.05.034, 2017. a, b, c
Remondi, B. W.: NGS Second Generation ASCII and Binary Orbit Formats and Associated Interpolation Studies, in: Permanent Satellite Tracking Networks for Geodesy and Geodynamics, edited by: Mader, G. L., 177–186, Springer Berlin Heidelberg, Berlin, Heidelberg, 1993. a
Springer, T., Dilssner, F., Escobar, D., Flohrer, C., Otten, O., Svehla, D., and Zandbergen, R.: NAPEOS: The ESA/ESOC tool for space geodesy, Geophys. Res. Abstr., EGU2011-8287, EGU General Assembly 2011, Vienna, Austria, 2011. a
Teunissen, P. J. and Amiri-Simkooei, A.: Least-squares variance component estimation, J. Geodesy, 82, 65–82, 2008. a
Watson, G.: Computing Helmert transformations, J. Comput. Appl. Math., 197, 387–394, https://doi.org/10.1016/j.cam.2005.06.047, 2006. a
Wermuth, M., Montenbruck, O., and Van Helleputte, T.: GPS high precision orbit determination software tools (GHOST), in: 4th international conference on astrodynamics tools and techniques, Madrid, Spain, 3–6, Citeseer, 2010. a
Wu, S. C., Yunck, T. P., and Thornton, C. L.: Reduced-dynamic technique for precise orbit determination of low earth satellites, J. Guid. Control Dynam., 14, 24–30, https://doi.org/10.2514/3.20600, 1991. a