Towards fully coupled Thermo-Hydro-Mechanical-Chemical (THMC) modelling in advanced reservoir engineering: GOLEM-PHREEQC

Effective geothermal resource development requires sophisticated computational tools integrating different physical and chemical processes. This work describes a novel coupling of GOLEM, an open source simulator for thermal-hydraulic-mechanical modeling based on the MOOSE multiphysics framework, with the PHREEQC geochemical solver. GOLEM solves coupled partial differential equations governing subsurface fluid flow, heat transfer, conservative mass transport, and mechanical deformation in complex geological environments. PHREEQC is a proven and widely adopted geochemical simulator in the scientific community. The coupling to GOLEM is achieved leveraging an efficient and original wrapper based on the IPhreeqc module. The newly developed coupling of flow, transport and geochemical reactions is validated against standalone PHREEQC by means of 1D RTM benchmarks including both equilibrium and kinetic mineral reactions. A further demonstration of the capabilities of the GOLEM-PHREEQC coupling is shown, on a 2D domain with three distinct geochemical zones.

1 Introduction

Exploration, planning and operational optimization of geothermal systems in porous and fractured media need powerful numerical tools that are able to capture and analyze an intricate network of coupled physical and chemical interactions between fluids and host rocks, each acting at different spatial and temporal scales (e.g., Jing et al., 2002; Rabemanana et al., 2003; Kiryukhin et al., 2004; Bächler and Kohl, 2005; André et al., 2006; Pandey et al., 2018). Such interactions are usually summarized as thermo-hydro-mechanical-chemical (THMC) processes, while the numerical frameworks enabling modelling of these systems are termed multiphysics. Reactive transport indicates the coupling of geochemical reactions with fluid flow and transport of solutes, including the feedbacks triggered by reactions, altering porous media and hence their permeability and mechanical characteristics. Established reactive transport simulators include RETRASO-CODEBRIGHT (Saaltink et al., 2004), CORE-2D (Samper et al., 2003), MIN3P (Mayer et al., 2002), HYTEC (Van der Lee et al., 2003), TOUGHREACT (Xu et al., 2011), PFLOTRAN (Mills et al., 2007), HP1 (Šimůnek et al., 2006) and CRUNCHFLOW (Steefel, 2009). A recent overview and intercomparison of RTM codes can be found in Steefel et al. (2014).

In recent years, several general-purpose and flexible multiphysics software frameworks able to couple arbitrary processes emerged, such as OpenFOAM^® (Greenshields and Weller, 2022), MOOSE (Gaston et al., 2009; Permann et al., 2020), FEniCS (Logg et al., 2012) and COMSOL Multiphysics^® (, ). Generally speaking, these allow users to conveniently define Partial Differential Equations (PDE) depicting the physical processes to be modelled, and the framework itself takes care of discretizing the PDEs and solving them numerically, thus leveraging robust linear and nonlinear solvers, adaptive temporal discretization, and effective spatial approximation methods implemented in advanced computational libraries such as PETSc (Balay et al., 2016) and Chombo (Trebotich et al., 2008).

Geochemical processes represent the usual computational bottleneck of reactive transport simulations and are the most complex to simulate given their high nonlinearity, the large number of variables and typically high number of parameters needed to model them. For this reason, it is in practice often preferable to leverage specialized geochemical solvers such as CHEPROO (Bea et al., 2009), PHREEQC (Parkhurst and Appelo, 2013), GEMS3K (Kulik et al., 2012), Orchestra (Meeussen, 2003) and Reaktoro (Leal, 2015). These specialized packages are then interfaced with the multiphysics simulators to add the capability of modelling geochemical reactions. Examples of this architecture are PHAST (Parkhurst et al., 2010), PHT3D (Prommer et al., 1999), PorousMedia4Foam (Soulaine et al., 2021), COMSOL-PHREEQC (Nardi et al., 2014), Firedrake-Reaktoro (Kyas et al., 2022), OpenGeoSys (He et al., 2015) and POET (De Lucia et al., 2021).

This contribution introduces the coupling between GOLEM (Cacace and Jacquey, 2017) and PHREEQC (Parkhurst and Appelo, 2013) through a novel, advanced wrapper based on the IPhreeqc module (Charlton and Parkhurst, 2011). GOLEM is a finite element application, built upon the MOOSE framework, specializing in thermal, hydraulic, and mechanical (THM) processes in fractured porous media. It solves the governing equations for single-phase fluid flow, heat transport, conservative mass transport, and mechanical deformation. PHREEQC functions as the chemical computation engine, handling equilibrium and kinetic reactions, cation exchange and surface complexation. In the following, we describe in detail the coupled simulator and provide a validation of the achieved coupling between hydrodynamic and chemical processes based on 1D benchmark scenarios involving mineral precipitation and dissolution. A further practical demonstration of current GOLEM-PHREEQC capabilities is also given, inspired by an Aquifer Thermal Energy Storage (ATES) application – a system that exploits subsurface aquifers for seasonal thermal energy storage and recovery. It is thereby showcased how the handling of geochemically heterogeneous zones is operative at this stage of development. ATES operations lead to rapid spatiotemporal variations in reservoir conditions, highlighting the necessity for high-fidelity simulation of geochemical interactions to ensure sustainable reservoir management.

2 Numerical Framework

The following sections detail the numerical architecture and integration strategy for the GOLEM-IPHREEQC coupling, emphasizing the distinct capabilities of each computational component.

2.1 GOLEM

GOLEM (Cacace and Jacquey, 2017) is an open source massively parallel computational platform for hydrothermal and geothermal modeling in heterogeneous reservoir systems, accommodating one-, two-, and three-dimensional problems through unified code architecture. GOLEM has been developed upon MOOSE (Permann et al., 2020), an advanced multiphysics framework in C++ based on the finite element method.

MOOSE itself employs rigorously tested computational libraries including libMesh (Kirk et al., 2006) for parallel finite element functionality and comprehensive solver suites based on PETSc (Balay et al., 2016), Trilinos (Heroux et al., 2005), and Hypre (Chow et al., 1998) for scalable linear and nonlinear equation solution. MOOSE provides out of the box hybrid parallelization capabilities, using Message Passing Interface (MPI) for distributed computing and multi-threading on shared-memory computers. Many computational features are built-in in MOOSE, such as adaptive mesh refinement, input/output using many scientific data formats. This modular architecture enables application developers to concentrate on physics formulation while maintaining streamlined code structures. Integrated MOOSE physics modules inherently support coupled THMC models. In particular, the Geochemistry module (Wilkins et al., 2021) is a promising alternative chemical solver. However, a more established, more flexible and better documented software such as PHREEQC was deemed more future-proof than this module, also in view of a significantly larger user base.

GOLEM itself is an application derived from MOOSE and adopts a similar modular philosophy, organizing distinct physical processes within dedicated computational modules that facilitate code maintenance and enhancement. GOLEM solves nonlinear thermal-hydraulic-mechanical processes and conservative mass transport by representing fractures, faults, and wellbores as discrete lower-dimensional discontinuous elements, while capturing nonlinear interactions and property-structure relationships. Examples of such relationships are: dependence of fluid density and viscosity on state variables (pressure, temperature, concentrations) alongside material property evolution reflecting reservoir changes (e.g., porosity-permeability correlations). More details and a comprehensive overview of the implemented numerics can be found in Cacace and Jacquey (2017).

For hydrodynamics and conservative transport, primary system variables are pore pressure P and volumetric solute concentrations C_i (where $i=\mathrm{1},N$ represents the total number of chemical species). According to Darcy's law for laminar flow, the pore pressure field is solved by combining the mass and momentum balances (Bundschuh and Suárez Arriaga, 2010) for the matrix as well as the lower-dimensional elements (wells and fractures) as:

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }b{S}_m{\displaystyle \frac{\partial P}{\partial t}}=-\mathrm{\nabla }\cdot b\mathit{q}+Q\text{(2)}& {\displaystyle }& {\displaystyle }\mathit{q}=-{\displaystyle \frac{\mathbf{K}}{{\mathit{\mu }}_f}}\cdot \left(\mathrm{\nabla }P-{\mathit{\rho }}_{\mathrm{f}}\mathit{g}\right)\end{array}$$

where P is the pore pressure; t is the time; S_m is the specific storage; Q is a source term; K is the permeability tensor; μ is the dynamic viscosity of the fluid; ρ_f is the fluid density; g is the gravitational acceleration vector; q is the fluid or Darcy velocity vector and b is a scale factor for fractures (aperture) and wells (diameter); b=1 for porous media. Advective-dispersive mass transport of ith solute is solved according to the second Fick's law:

$$\begin{array}{}\text{(3)}& b{\displaystyle \frac{\partial C_i}{\partial t}}=-\mathrm{\nabla }\cdot b\left(\mathit{q}{C}_i-\mathbf{D}\mathrm{\nabla }{C}_i\right)+Q_i\end{array}$$

In case of non-reactive (conservative) mass transport, Q=0. The effective hydrodynamic dispersion tensor D is defined as:

$$\begin{array}{}\text{(4)}& \mathbf{D}=\left(D_m+{\mathit{\alpha }}_T\Vert \mathit{q}\Vert \right)I+\left({\mathit{\alpha }}_L-{\mathit{\alpha }}_T\right){\displaystyle \frac{\mathit{q}{\mathit{q}}^{\mathit{T}}}{\Vert \mathit{q}\Vert }}\end{array}$$

This system of coupled nonlinear equations is solved numerically by GOLEM in a fully coupled, full implicit approach, exposing to the user many capabilities offered by the MOOSE framework, including appropriate spatial discretization schemes, several choices for time-stepping and temporal integration approach, as well as many iterative solvers and preconditioners. Each of these aspects plays a critical role in ensuring the accuracy, stability, and efficiency of the solution process. For the sake of brevity, readers interested in a comprehensive discussion are referred to Cacace and Jacquey (2017) for further elaboration on the numerical methods and techniques employed.

2.2 PHREEQC

PHREEQC (Parkhurst and Appelo, 2013) is a multi-platform open source simulator for aqueous geochemistry developed by US Geological Survey. It can be considered as a de facto standard in the scientific community given its longevity and comprehensive modelling capabilities: it can namely model aqueous speciation, incorporating various activity models and thermodynamic databases; redox reactions; mineral precipitation and dissolution under both equilibrium and kinetic control; ion exchange and surface complexation, implementing several phenomenological models therefore; and finally, isotope fractionation and one-dimensional reactive transport problems. PHREEQC, implemented in C++, ships with several thermodynamic databases based on a variety of activity correction models, including extended Debye-Hückel, Pitzer and Specific Ion Interactions. Geochemical processes in PHREEQC are described in terms of Law of Mass Action, which results in the formulation of nonlinear equilibrium system of equations subjected to charge and mass balance. Iterative Newton-Raphson method coupled with convex optimization algorithm are employed to solve the thermodynamic equilibrium system of equations; kinetic processes are integrated through Runge-Kutta or, for particularly stiff problems, the cvode solver. An important implementation characteristic is that all aqueous chemical reactions, including redox processes, are considered at local thermodynamic equilibrium. Kinetic control is hence only possible for heterogeneous reactions. This also means that all redox couples in solution are always simultaneously at the same potential.

PHREEQC embeds an interpreter for the BASIC programming language, through which the user can define arbitrary kinetic laws in form of small programs, and specify custom output and computations. The software operates on textual input scripts, with a simple syntax organized in blocks with defined keywords. The results of computations are returned in form of formatted text file or, optionally, in tabular form in an additional text file, if requested by the user. Graphical User Interfaces (GUI) are available for PHREEQC, but under the hood they all leverage the text-based input-output.

2.3 IPhreeqc and the POET wrapper

To streamline integration and connectivity with external programming languages and other computational tools, the PHREEQC authors developed the IPhreeqc module (Charlton and Parkhurst, 2011) and the PhreeqcRM library (Parkhurst and Wissmeier, 2015). PhreeqcRM facilitates the integration of PHREEQC into reactive transport simulators, offering integrated parallelization (both MPI and OpenMP) and unit conversions. However, its API (Application Programming Interface) relies primarily on PHREEQC input scripts, which on the one hand provides benefits for users experienced with the platform, but on the other is not optimal regarding the efficiency of data exchange and computational performance. IPhreeqc is a modular wrapping of the PHREEQC core and eases the coupling of the simulator to other applications, in this case specifically programming languages such as python (e.g., phreeqpy https://www.phreeqpy.com/, last access: 22 December 2025) or R (De Lucia and Kühn, 2021).

The development of the POET simulator (POtsdam rEactive Transport, De Lucia et al., 2021; Lübke et al., 2025) led to the implementation of an original wrapper for the IPhreeqc module. This new interface, named litephreeqc, is designed to eliminate, after initialization, the need for parsing or modifying PHREEQC input scripts to perform geochemical calculations. Instead, it operates directly on the in-memory data structures of the core PHREEQC engine, resulting in a much more efficient data transfer which is of particular significance in the context of large-scale simulations. The users specify the actual chemical systems, including solutes and mineral phases, by providing actual PHREEQC scripts, hence familiar to many practitioners. The POET wrapper implemented in litephreeqc is leveraged for the coupling of GOLEM with PHREEQC, as described in more detail in the next section.

2.4 The GOLEM-PHREEQC Coupling

As specified in the previous sections, GOLEM handles the thermal and fluid dynamics throughout the reservoir, whereas PHREEQC manages the geochemical processes. At the time of writing, dissolution and precipitation reactions both under equilibrium and with kinetic control, cation exchange and, partially, surface complexation are handled by the litephreeqc wrapper and hence usable in the GOLEM-PHREEQC coupling.

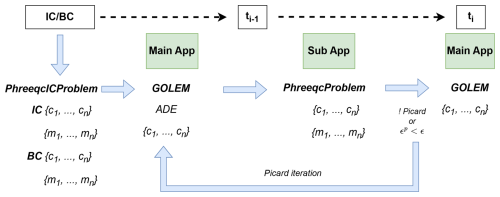
Information exchange between GOLEM and PHREEQC relies on the MOOSE Transfer System framework, offering multiple mesh-to-mesh communication approaches (including nearest node assignment, projections, interpolations and additional methods). Data exchange protocols are typically designed to remain independent of the physical meaning of associated degrees of freedom (dof) between source and destination meshes. Input/output communication between GOLEM and PHREEQC is ensured by correlating each PHREEQC calculation, one per GOLEM elemental dof, with the finite element grid employed by GOLEM. Data reading/writing between solution arrays to/from GOLEM and PHREEQC occur at the elemental scale using the corresponding element identifier, which marks the associated dof of the active calculation. GOLEM and PHREEQC are coupled through fixed point (Picard) iteration methodology utilizing bidirectional data exchange of solute concentrations across timesteps, leveraging MOOSE's MultiApp infrastructure. The user can specify whether the operator-splitting coupling of transport and chemistry is to be solved iteratively (SIA, Sequential Iterative Approach) or non-iteratively (SNIA).

A schematic representation of the coupling is given in Fig. 1. The chemical problems assigned to initial (IC) and boundary conditions (BC) are specified by the user through baseline PHREEQC input scripts and a thermodynamic database. The litephreeqc wrapper runs all different geochemical problems and builds a tabular data structure containing all data needed by GOLEM to initialize the kernels for the transient transport problems. The application then updates concentrations due to transport before passing the modified data at runtime to the PHREEQC transient sub-calculation. The latter executes a batch reactive chemistry update of solutes and minerals before returning the affected variables to the transient GOLEM application. Hybrid parallelization of PHREEQC calculations utilizes the same MPI groups as GOLEM, implementing loop parallelization of the geochemical reactive calculations based on input processors through a specialized MOOSE ExternalProblem class.

Figure 1 Schematic representation of the GOLEM-PHREEQC coupling, where C_i are solutes and M_i are mineral and gas phases.

3 Validation of GOLEM-PHREEQC coupling

The validation hereby presented is based on a classical isothermal 1D reactive transport problem initially proposed by Engesgaard and Kipp (1992), and which has traditionally been employed as a benchmark in many instances (He et al., 2015; Leal et al., 2020; De Lucia et al., 2021). The simulated system includes carbonate dissolution and precipitation within a water-saturated column of porous medium initially at equilibrium with calcite CaCO₃, hence with an initial pH of 9.91. The medium in the column has a porosity φ=0.32, and its length set to 0.5 m. A 1 millimolal (mmol kgw⁻¹) magnesium chloride (MgCl₂) solution at pH = 7 and 25 °C is injected into the column for 350 min (∼5.8 h) at a constant rate corresponding to a Darcy velocity (q) of $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{6}}$ m s⁻¹. The arrival of the MgCl₂ solution triggers the dissolution of calcite and the transient precipitation of dolomite, magnesium-calcium carbonate CaMg(CO₃)₂. Once calcite in a given grid element is completely dissolved, also dolomite becomes undersaturated and redissolves.

For GOLEM, a quasi-3D computational domain measuring 0.5 m in length divided into 100 uniform elements with a cross-sectional area A=0.1 m², was chosen as spatial discretization. Figure 2 visualizes the simulation grid for the benchmark. A longitudinal dispersivity D_L=0.0067 m and a timestep of 525 s were used in all simulations.

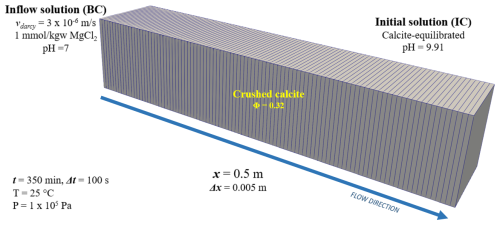
Figure 2 Mesh and model setup used for validation of the GOLEM-PHREEQC coupling against PHREEQC's own 1D reactive transport capability.

Thermodynamic parameters for hydrolysis, aqueous speciation, and dissolution/precipitation processes involving Mg, Ca, Cl, and carbonate species were obtained from version 12/07 of the PSI/NAGRA chemical thermodynamic database (Thoenen et al., 2014). Both initial and inlet solutions are equilibrated with atmospheric oxygen partial pressure of O_2(g) of 10^−0.68 atm or 0.221×10⁵ Pa to maintain pe at positive values. Porosity changes throughout the simulation are neglected.

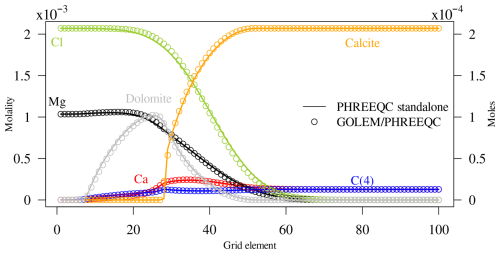
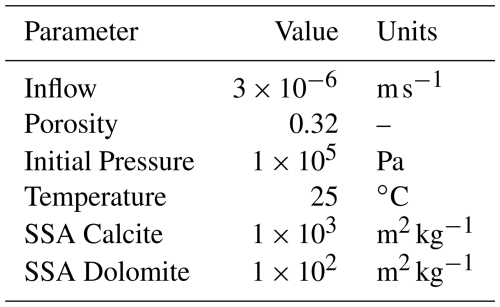
Figure 3 shows a comparison of results from GOLEM-PHREEQC and the corresponding models computed with the 1D transport feature of PHREEQC at the end of simulation time for the case with both minerals considered at equilibrium. The results clearly demonstrate that the MgCl₂ solution front has advanced ∼0.3 m into the column, causing calcite dissolution and dolomite precipitation. Total aqueous concentrations and solid phase profiles from GOLEM-PHREEQC show excellent agreement with the results from PHREEQC. The small discrepancies arise from the different spatial discretizations and numerical solution schemes for transport implemented in the two simulators: FEM for GOLEM and explicit Euler (forward time) finite differences scheme for PHREEQC. The same exercise is repeated including kinetic control of mineral reactions both for dissolution and precipitation. Here, the phreeqc.dat chemical thermodynamic database is used, while kinetic rate expressions for dolomite and calcite are derived from Palandri and Kharaka (2004). The sole parameter needed by the rate expression is the specific surface area SSA, which was assigned as 1×10³ and 1×10² m² kg⁻¹ for finely-ground calcite and dolomite, respectively. A summary of the parameters employed to inform the simulations is given in Table 1. The results of kinetic simulations are displayed in Fig. 4.

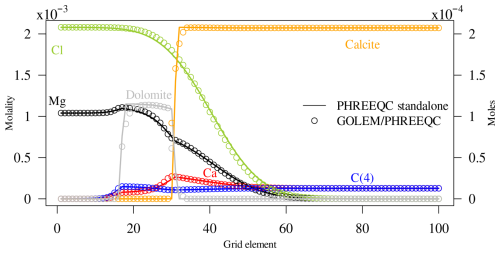
Figure 3 Validation of the GOLEM-PHREEQC coupling against standalone PHREEQC, equilibrium simulations.

Table 1 Parameters of the 1D benchmark used to validate the GOLEM-PHREEQC coupling against PHREEQC in both equilibrium and kinetic models.

Figure 4 Validation of the GOLEM-PHREEQC coupling against PHREEQC, kinetic simulations.

These two benchmarks, while being computationally light – both simulations run in under ten seconds – confirm the reliability of reactive transport outcomes achieved through the new GOLEM-PHREEQC coupling compared to standalone PHREEQC calculations. Both equilibrium and kinetic reaction mechanisms are precisely replicated.

3.1 An Example of Zone-Heterogeneous 2D RTM Simulation: ATES

To further illustrate the capabilities of our new implementation in handling heterogeneity typical of real-world subsurface systems, an additional simulation was conducted. The model is inspired by the geological and hydrogeochemical characteristics of the reservoir encountered at approximately 250 m depth by the ATES research drilling (Gt BChb 1/2015) in Berlin-Charlottenburg (Blöcher et al., 2024). The 2D model, simplifying the original reservoir geometries, comprises two highly permeable sandy layers, each 1 m thick of Tertiary to Upper Triassic age, separated by a 0.5 m thick aquitard. The model setup is shown in Fig. 5.

Geochemically and hydrodynamically, the three layers are initialized as distinct and independent domains, each with unique transport properties and specific solute and mineral assemblages (Table 2). The central aquitard is relatively inert due to the slow dissolution kinetics of quartz, while the sandy layers contain more reactive minerals, implemented either as kinetic or equilibrium phases. Pyrite (FeS₂) and kaolinite (Al₂Si₂O₅(OH)₄) are the primary reactive phases of interest.

From an engineering perspective, the main objective of this simulation is to test the hypothesis proposed by Regenspurg et al. (2020) that the anomalous Al release observed during previous hydraulic testing may have been triggered by the injection of oxidizing fluids. Such conditions would promote pyrite oxidation, leading to proton generation, local acidification, and the subsequent dissolution of aluminum-bearing silicates – particularly clay minerals such as kaolinite. To further explore the fate of iron (Fe) released during pyrite oxidation, the model includes the potential for siderite (FeCO₃) precipitation in the lower layer, driven by carbonate availability following calcite dissolution. This process is of particular interest as pore clogging due to secondary mineral precipitation may reduce long-term system performance.

The model domain measures 10 m × 2.5 m and is discretized into a grid of 1000 × 50 cells, resulting in 50 000 dof. The domain is subdivided into three distinct units – upper layer, middle layer, and lower layer – corresponding to the previously described lithological blocks. The heterogeneous hydraulic and geochemical properties of the layers are summarized in Fig. 5 and Table 2. Fluid properties (density, viscosity) are constant and representative of reservoir conditions, corresponding to a temperature of 17 °C and a pressure of 2.1 MPa. Material properties such as porosity and permeability vary between layers to simulate heterogeneous transport behavior. A fixed overpressure of 0.05 MPa is applied at the left model boundary to represent oxidizing fluid injection. Both dispersivity and hydrodynamic diffusion coefficients are set to zero throughout the domain to isolate advective transport effects.

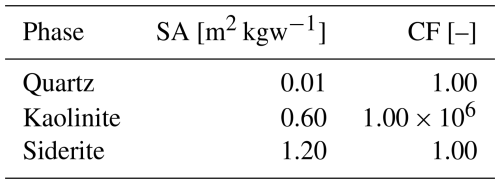
In terms of fluid composition, each layer is initially saturated with a specific set of minerals making use of the phreeqc.dat thermodynamic database. The middle layer is equilibrated with quartz, reflecting its relatively inert character. The upper layer is initially equilibrated with pyrite and kaolinite, whereas the lower layer includes calcite in addition to these phases. This results in elevated concentrations of dissolved ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ and a pH of 9.96 in the bottom layer, compared to the more neutral conditions observed in the upper and middle layers. The injected 0.3 millimolal (mmol kgw⁻¹) NaCl solution entering from the left boundary is initially equilibrated with an oxygen partial pressure of O_2(g) of 10^−1.00 atm and a partial pressure of CO_2(g) of 10^−3.38 atm, resulting in a highly positive pe of 15.66 and a moderately acidic pH of 5.58. Pyrite and calcite are modeled as equilibrium phases, while the remaining minerals are under kinetic control. Rate laws were sourced from Marty et al. (2015); the corresponding parameters – initial surface area SA [m² kg⁻¹] and correction factor CF – are summarized in Table 3. Secondary precipitation of siderite is allowed only in the bottom layer, while precipitation of kaolinite and calcite is suppressed throughout the domain. The injection of oxidizing fluids from the inlet boundary results in a non-uniform transport front due to the hydraulic contrast among the layers. Darcy velocity q ranges from $\mathrm{1.12}\times {\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹ in the bottom layer to as low as $\mathrm{1.10}\times {\mathrm{10}}^{-\mathrm{12}}$ m s⁻¹ in the middle one, with Cl, which acts conservatively in this simulation, travelling between 4.5 and 7 m within the domain during the simulation period (Fig. 6).

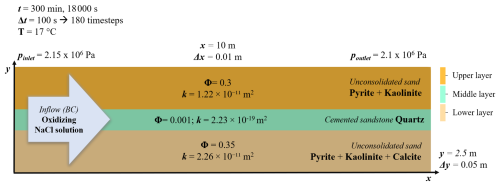
Figure 5 Mesh and model setup used for the heterogeneous simulation. The injected solution is equilibrated with 0.1 atm partial pressure of oxygen, triggering pyrite oxidation and release of protons in the system.

As expected, in the two main reactive layers, the injected fluid triggers pyrite oxidation, releasing ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, Fe²⁺, and H⁺ into the fluid phase. These more acidic conditions, together with the undersaturation of kaolinite in the injected fluids, induce kaolinite dissolution and the subsequent release of Al and Si. In the lower layer, calcite dissolution releases carbonate, which combines with Fe²⁺ from pyrite oxidation and leads to siderite precipitation (Fig. 6). Although only limited quartz dissolution occurs in the central aquitard, the fluid chemistry evolves due to solute contributions from the bounding layers throughout the simulation.

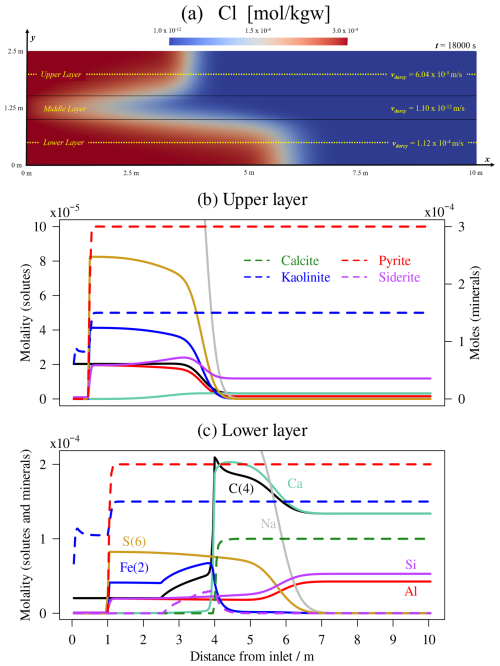
Figure 6 (a) Map of total dissolved Cl concentrations at the end of simulation time. The yellow dotted lines represent the location of the profiles displayed in the other two images. (b) Concentration profiles of relevant solutes and minerals in the upper layer. Minerals, represented with dashed lines, refer to the y-axis on the right; (c) Profiles of relevant solutes and minerals in the lower layer.

Table 2 Initial geochemical setup used for the heterogeneous simulation (UL = Upper Layer; ML = Middle Layer; LL = Lower Layer; IS = Inlet Solution).

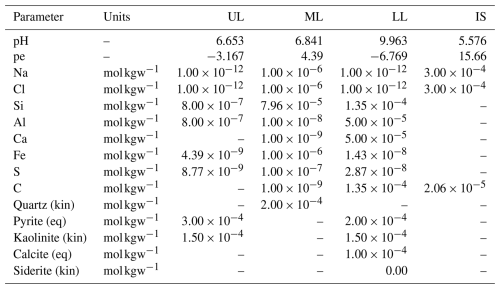
Table 3 Kinetic parameters used the heterogeneous simulation (SA = Initial Surface Area; CF = Correction Factor).

This simulation runs in ∼ 60 min using 16 cores on a compute server equipped with Intel Xeon CPU at 3.20 GHz. This example further demonstrates the capabilities of the GOLEM-PHREEQC implementation to handle reactive transport in hydraulically and geochemically heterogeneous systems, and represents a first step towards the analysis of complex real-world reservoir dynamics through open source numerical modelling.

4 Outlook and Future Developments

While still at an early stage of development, the GOLEM-PHREEQC coupling supports 1D/2D/3D simulations of fluid flow, rock mechanics and reactive transport, including mineral dissolution & precipitation processes, cationic exchange and partial support to surface complexation. A simple mechanism to assign grid elements to distinct, heterogeneous geochemical zones is built in. While not yet fully validated at the time of writing, the coupling between heat transport and chemical reactions is also functioning. Heat transport is integral to GOLEM and used only as input for geochemical simulations in our coupling, since PHREEQC does not compute excess reaction heat.

The capability to utilize parallelization and high-performance computing additionally enables effective simulation of large, heterogeneous systems. Furthermore, the open source nature of this software allows users to examine, modify, and expand its source code to address specific research or engineering requirements, removing constraints and ambiguities frequently encountered with proprietary software. The successful validation establishes the groundwork for the subsequent development phase, focused on representing more sophisticated dynamic interactions between geochemical reactions and subsurface transport phenomena, notably including feedbacks to other subprocesses.

A full-fledged THMC simulator should incorporate feedbacks between the different physical and chemical processes. A first example of feedback under development is the dynamic update of permeability following changes in porosity due to mineral alterations. The well-established Kozeny-Carman relationship (Kozeny, 1927; Carman, 1937, 1956) is a widely adopted empirical correlation often used in reactive transport simulators to represent the feedback of chemistry on hydrodynamics. Many further feedback mechanisms still need to be implemented to achieve a more realistic description of subsurface processes, i.e., change in mechanical characteristics of the medium following chemical degradation of mineral components. The full feedback of chemical reactions on the hydrodynamic properties of the fluid (density, viscosity, heat capacity) is also subject of ongoing work, allowing fluid properties such as density and viscosity to change in response to chemical modifications in the system. This can be achieved either leveraging the aqueous model implemented in PHREEQC or by user-specified equations of state.

Finally, support for fractured reservoir systems is planned, enabling simulation of preferential flow channels and their interaction with reactive mechanisms. Concurrent investigations are examining the viability of integrating Reaktoro (Leal, 2015) into the GOLEM framework as an additional geochemical engine. This would provide enhanced geochemical modeling capabilities, especially for multiphase systems and advanced kinetic formulations, and leverage the On Demand Machine Learning (ODML) approach embedded in this simulator (Leal et al., 2020). The recently published general interface Alquimia (Molins et al., 2025) represents also an interesting further option for the extension of GOLEM, since it promises the ability to swap different specialized geochemical solvers with limited programming efforts and will be explored in future.

5 Conclusions

This paper presents the latest developments in the ongoing implementation of the GOLEM-PHREEQC coupling for reactive transport modeling in fully saturated heterogeneous media. With a fully functional integration of both equilibrium and kinetic reactions within heterogeneous domains, our effort is now focused on incorporating the full PHREEQC capabilities and implementing the dynamic feedbacks across processes. The open source GOLEM-PHREEQC framework demonstrates strong potential as a robust alternative to commercial software solutions for simulating multiphysics (THMC) advective-dispersive reactive transport processes in complex geothermal systems. These attributes support the broader goal of promoting the widespread adoption of multiphysics modeling platforms within the geoscientific and engineering communities, and encourages a more inclusive advancement of computational modeling practices. In addition, extending the framework to support other geochemical solvers through unified interfaces would further enhance its versatility and allow for comparative benchmarking across different modeling approaches.