Physics-based numerical evaluation of High-Temperature Aquifer Thermal Energy Storage (HT-ATES) in the Upper Jurassic reservoir of the German Molasse Basin

Concepts of High-Temperature Aquifer Thermal Energy Storage (HT-ATES) (> 50 °C) are investigated in this study for system application in the Upper Jurassic reservoir (Malm aquifer) of the German Molasse Basin (North Alpine Foreland Basin). The karstified and fractured carbonate rocks exhibit favourable conditions for conventional geothermal exploitation of the hydrothermal resource. Here, we perform a physics-based numerical analysis to further assess the sustainability of HT-ATES development in the Upper Jurassic reservoir. With an estimated heating capacity of approx. 19.5 MW over half a year, our approach aims at determining numerically the efficiency of heat storage under the in situ Upper Jurassic reservoir conditions and projected operation parameters. In addition, the hydraulic performance of the HT-ATES system is further evaluated in terms of productivity and injectivity index.

The numerical models build upon datasets from three operating geothermal sites at depths of approx. 2000–3000 m TVD, located in a subset of the reservoir dominated by karst-controlled fluid fluxes. Commonly considered as a single homogeneous unit, the 500 m thick reservoir is subdivided into three discrete layers based on field tests and borehole logs from the three considered sites. The introduced vertical heterogeneity with associated layer-specific enhanced permeabilities allows to examine potentially arising favourable heat transfer, and in combination with the facilitated high operation flow rates (100 kg s⁻¹) to evaluate thermal recoveries in the multilayered reservoir. All simulations account for fluid density and viscosity variation based on thermodynamically consistent equations of state (EOS).

Computation results reveal that the reservoir layering induces preferential fluid and heat migration primarily into the high-permeability zone, while thermal front propagation into the lower permeable rock matrix is inhibited. The simulations further display a gradual temperature increase in the warm wellbore and its surrounding host rock, and a consequent progressive improvement in the heat recovery efficiency. Despite the elevated permeability that may trigger advective heat losses, heat recovery factor values range from approx. 0.7 over the first year of operation to over 0.85 after 10 years of operation. An additional scenario is examined with fluid injection solely in the high permeable zone, in order to quantify potential enhancement in the recovery efficiency by omitting fluid injection in the lower-permeability layers where heat propagation is diminished. This is due to the geometrical shape of the thermally perturbed rock volume as heat losses occur during thermal equilibration between injected fluid and reservoir rock, as well as at the contact-surface area between propagating thermal front and adjacent rock matrix. Results suggest that under the stratified reservoir configuration, additionally constrained by the selected spatial distribution of rock properties, heat storage performed only into the upper high-permeability zone corresponds to an improved thermal performance. Simulation results further indicate that density-induced buoyant fluxes, which would considerably decrease thermal efficiencies are inhibited in the system, and the prevailing heat transport mechanism is forced convection.

1 Introduction

The Upper Jurassic reservoir of the North Alpine Foreland Basin comprises the most significant target horizon for conventional geothermal exploitation of the hydrothermal resource in the German Molasse Basin, southern Germany. This stems from the combined effect of favourable reservoir temperature and in situ hydraulic conditions (Steiner et al., 2014), while the reservoir conditions and geographical location, close to the Munich metropolitan area, turn it into a significant asset to contribute towards covering the high local energy demand. As manifesting a southward dipping towards the Northern Alpine Front, the karstified and fractured carbonate rocks attain depths of up to 6 km, and reservoir temperatures rise from approx. 40 °C in the north to up to 160 °C in the south (Flechtner et al., 2020; Weber et al., 2019). In the area of Munich, the reservoir lays between 1.5 and 3 km, with reservoir temperatures as observed in geothermal wells varying between 70 and 120 °C. Characterized by considerable spatial heterogeneity, the presence of distinct structural features, as for instance karst zones or fractures/faults, introduces physical anisotropy in the system, and together with the reservoir matrix marks a spatial transitioning of the fluid-flow control across the different reservoir segments.

Despite the extensive and cross-disciplinary investigation of the reservoir towards its integrative characterization as well as the continuous development of new geothermal projects, its suitability for thermal energy storage has not been yet sufficiently analyzed. In parallel, concepts of High-Temperature Aquifer Thermal Energy Storage (HT-ATES) (> 50 °C) are currently being increasingly considered by geothermal plant operators for system application in the German Molasse Basin. HT-ATES systems yield considerable capacity for thermal energy storage by integrating seasonal phases of charging and discharging a reservoir through, commonly, a well doublet. During periods of available excess energy, the surplus energy is transferred into reservoir fluid produced from a well, and subsequently stored in the reservoir through a different well. In turn, during periods of high energy demand, the operation cycle is reversed and the stored fluid volume is produced, while after heat extraction the produced fluid volume is re-injected into the reservoir. In the area of Munich, potential thermal energy sources may span from combined heat and power (CHP) or geothermal to waste incineration plants, while the HT-ATES systems can be deployed to cover peak loads of energy demand, and can additionally comprise redundancy components of the energy network systems. This framework provided the stimulus to our present study, in which we aim at quantifying, via physics-based numerical modelling, the system performance with respect to HT-ATES concept development and at providing a predictive assessment of HT-ATES application in the Upper Jurassic reservoir.

The availability and access to a variety of datasets facilitates the development of a physics-based numerical approach to predict the HT-ATES-system behaviour under the in situ reservoir conditions and a reservoir-specific operation scheme. The presented analysis emphasizes on the central area of Munich, relying on discrete data derived from three operating geothermal plants, all characterized by karst-dominated hydrodynamics. In this regard, the developed synthetic numerical models populated with encountered reservoir rock properties are considered to represent efficiently the Upper Jurassic reservoir in the selected subsection of the Molasse Basin.

We perform coupled numerical simulations of fluid flow and heat transport to capture and describe the physical processes induced by the storage of high-temperature fluids into the reservoir. More specifically, we compare two ATES-system configurations, differentiated by the penetration-extent of the wellbores into the reservoir. In the first model (reference model hereafter), the wells intersect the entire 500 m reservoir thickness, whereas in the second model the wells are hydraulically connected only with the upper 140 m high-permeability reservoir-zone (karst model hereafter). The hydraulic performance of the two system designs is evaluated in terms of productivity and injectivity indexes, while the thermal performance is assessed based on the computed heat recovery factor. Consequently, conclusions on the efficiency of the two distinct HT-ATES-system configurations are deduced under the investigated stratified reservoir setting. In a broader context, the presented comparative numerical approach additionally exemplifies and addresses the transient relative impact of the contributing convective and conductive heat transfer components, both in terms of thermal energy distribution during fluid injection as well as in terms of induced heat losses during storage under such multilayered targeted reservoirs.

2 Methodology

2.1 Numerical approach

The coupled thermal-hydraulic numerical simulations presented in this study have been performed with GOLEM (Cacace and Jacquey, 2017), a numerical simulator developed for coupled thermal-hydraulic-mechanical-chemical problems in fractured and porous media. GOLEM builds upon the parallel, object-oriented finite element framework MOOSE (Permann et al., 2020). Several studies (e.g. Sheldon et al., 2021; Collignon et al., 2020; Schout et al., 2014) demonstrate the impact that fluid density-induced buoyant fluxes arising during ATES operation exert on the estimated thermal performance of the system. To consider such potential effects, the numerical simulations further account for density and viscosity variation based on equations of state (EOS) derived from 2008 releases of the IAPWS (International Association for the Properties of Water and Steam) thermodynamic property formulations (IAPWS, 2008a, b).

2.2 Governing equations

The following conservation laws of mass, energy and momentum are deployed to derive the governing partial differential equations for the coupled thermal-hydraulic problem (Nield and Bejan, 2006). Those are solved with respect to the state variables pore fluid pressure p_f, and temperature T.

The continuity equation of mass for the liquid phase in a saturated porous medium reads as:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\partial \left(n{\mathit{\rho }}_{\mathrm{f}}\right)}{\partial t}}+\mathrm{\nabla }\cdot \left({\mathit{\rho }}_{\mathrm{f}}{\mathit{q}}_D\right)=Q_{\mathrm{f}},\end{array}$$

where ρ_f denotes the fluid density, n the porosity, q_D the Darcy fluid flux, and Q_f corresponds to a source/sink mass term.

Under the assumption of local thermodynamic equilibrium between the solid and fluid phase, the energy balance equation considering both advective and conductive components of heat transfer reads as:

$$\begin{array}{}\text{(2)}& T{\displaystyle \frac{\partial {\left(\mathit{\rho }{c}_p\right)}_{\mathrm{b}}}{\partial t}}+{\left(\mathit{\rho }{c}_p\right)}_{\mathrm{b}}{\displaystyle \frac{\partial T}{\partial t}}+\mathrm{\nabla }\cdot \left({\mathit{\rho }}_{\mathrm{f}}{c}_{p,\mathrm{f}}{\mathit{q}}_{D}T-{\mathit{\lambda }}_{\mathrm{b}}\mathrm{\nabla }T\right)=\dot{H},\end{array}$$

where $(\mathit{\rho }{c}_p{)}_{\mathrm{b}}=n{\mathit{\rho }}_{\mathrm{f}}{c}_{p,\mathrm{f}}+(\mathrm{1}-n){\mathit{\rho }}_{\mathrm{s}}{c}_{p,\mathrm{s}}$ is the bulk specific heat capacity of the system, with ρ_f and ρ_s the fluid and solid density, c_p,f and c_p,s the fluid and solid specific heat capacity, ${\mathit{\lambda }}_{\mathrm{b}}=n{\mathit{\lambda }}_{\mathrm{f}}+(\mathrm{1}-n){\mathit{\lambda }}_{\mathrm{s}}$ the bulk thermal conductivity of the porous medium, with λ_f and λ_s the fluid and solid thermal conductivity, and $\dot{H}$ the heat source/sink term.

The mass and energy equations are coupled through Darcy's law that expresses the conservation of momentum:

$$\begin{array}{}\text{(3)}& {\mathit{q}}_D=-{\displaystyle \frac{\mathit{k}}{{\mathit{\mu }}_{\mathrm{f}}}}\cdot \left(\mathrm{\nabla }{p}_{\mathrm{f}}-{\mathit{\rho }}_{\mathrm{f}}\mathit{g}\right),\end{array}$$

where k is the permeability tensor, μ_f the dynamic fluid viscosity, and g the gravitational acceleration tensor.

2.3 Numerical model

Spatially characterized by significant structural and geological heterogeneity, the reservoir is considered compartmentalized into three principal segments with respect to its primary fluid-migration control. This compartmentalization stems from investigations that point to the presence of different hydraulically conductive features across the Molasse Basin, varying from reservoir matrix in the north or karst zones beneath the greater area of Munich to fractures and faults in the south. The present numerical analysis emphasizes on a reservoir-subset beneath the central area of Munich controlled mainly by karst-dominated hydrodynamics, and further delineated by favourable reservoir conditions for storage of high-temperature fluids. We base the geological reconstruction on three geothermal systems, which operate within this reservoir subsection and on diverse datasets to constrain the multiphysics synthetic models, whereas a reservoir-specific operation design is adopted.

Table 1 Rock properties assigned to the reference and karst numerical model.

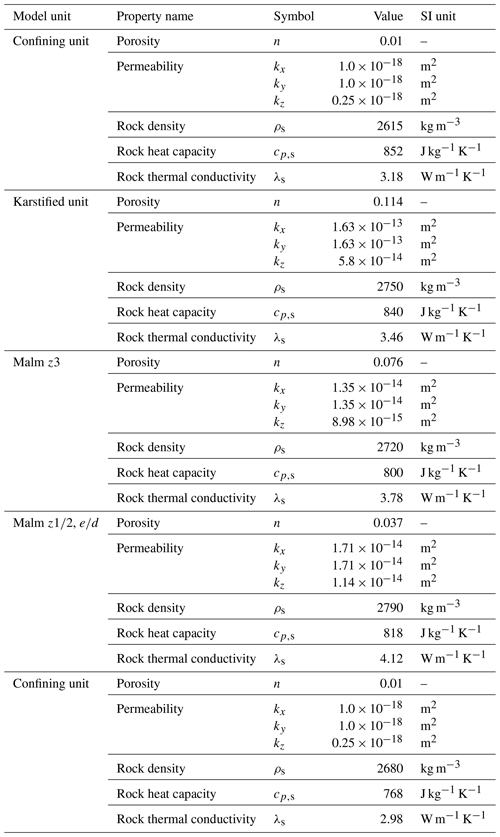
Deriving from available borehole log data of the three sites, the principal geometries of the model domain (Fig. 1) are defined. The model dimension is 1 km × 1 km in the horizontal direction and 900 m in the vertical direction, while the reservoir attains its average 500 m thickness. Commonly considered as a single homogeneous unit, the reservoir is subdivided into three discrete layers. The shallower 140 m thick reservoir unit consisting of the Purbeck, Bankia and Malm $z\mathrm{4}/\mathrm{5}$ formations represents a highly-conductive karstified unit. This unit is underlain by the 60 m lower-permeability Malm z3 formation, followed by the Malm $z\mathrm{1}/\mathrm{2}$ and $e/d$ sequences, integrated into a single 300 m thick domain. This introduced vertical heterogeneity with associated layer-specific enhanced permeabilities allows to examine favourable heat transfer into the different zones, and evaluate the HT-ATES system performance under this stratified reservoir setting. Two confining layers, each 200 m thick, on top and bottom of the reservoir disconnect it hydraulically from overlying and underlying sequences. Nevertheless, thermal energy losses in the form of conductive heat transfer from the reservoir to the confining units can occur. Average values of reservoir rock and fluid properties as available from a series of hydraulic tests, borehole logs and rock core analyses, are listed in Tables 1 and 2, respectively, and we deploy these values to populate each model unit in the present study.

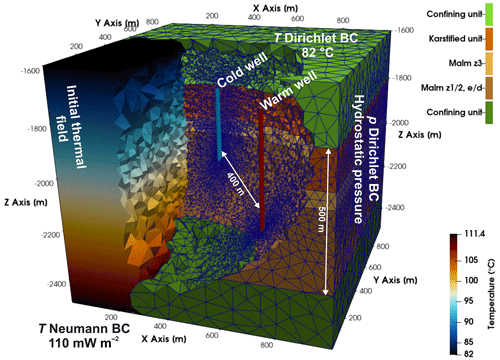
Figure 1 Model domain, modelled units and thickness of the reservoir as well as generated finite element mesh. Depth of penetration of the two wells of the reference model (i.e. 500 m), well distance and placement on the model diagonal, and local higher spatial discretization of the matrix in the vicinity of the wells are also illustrated. Imposed hydraulic and thermal boundary conditions, and initial undisturbed temperature field are further displayed.

Table 2 Fluid properties assigned to the reference and karst numerical model.

Heat storage is assigned through two vertical wells (Fig. 1), numerically represented by 1D elements, and termed as “warm” (storage of high-temperature fluid) and “cold” (fluid injection after heat extraction) well. As stated before, two HT-ATES system configurations are analyzed and compared. A reference model where fluid injection and production occurs along the entire 500 m reservoir thickness (Fig. 1), and a karst model where we limit the well sections to penetrate only into the upper 140 m karstified unit. In both case studies we maintain the well location on the model diagonal with a specified 400 m well distance, approx. twice the estimated thermal radius (Doughty et al., 1982) under the hypothesis of assuming main inflow primarily into the thinnest Malm z3 reservoir zone. Implemented reservoir rock properties, boundary conditions (BCs) and assigned operation scheme are also kept identical in the two models.

The injection of high-temperature fluid takes place through the warm wellbore at 140 °C during the referred to as “charging phase”. In parallel, reservoir fluid is produced from the cold well comprising the working fluid of the heat storage operation. Subsequently, the operation mode is reversed. The stored fluid volume is produced from the warm well during the termed as “discharging phase” and simultaneous injection after heat extraction occurs in the cold wellbore at 95 °C, i.e. the average reservoir temperature in those depths. We consider a consecutive 6 months duration of the charging phase and an equal duration of the discharging phase, with no operational pauses, in consecutive semi-annual cycles over a continuous 10 years of simulation time. The fluid injection and production rate in both wells is identical and equal to 100 kg s⁻¹, ensuring conservation of mass in the system. Therefore, a comparable storage capacity of approx. 19.5 MW over half a year characterizes the two HT-ATES systems.

The unstructured tetrahedral numerical mesh is generated with the software MeshIt (Cacace and Blöcher, 2015). The mesh resolution of the vertical model boundaries is set to 100 m, whereas that of the horizontal boundaries is 120 m. The degree of mesh refinement in the different reservoir units is specified in dependence to their thickness to ensure stability in the computation, as well as sufficient numerical resolution, thus providing physically consistent predictions of the state distribution within each single unit. In this regard, the upper surface of the karstified unit is discretized with 70 m, the top and bottom of the thinner Malm z3 with 35 m, whereas the bottom surface of the Malm $z\mathrm{1}/\mathrm{2}$, $e/d$ is assigned a 100 m resolution. A higher spatial discretization of 2 m is assigned in the reservoir matrix adjacent to the wells (Fig. 1) due to the anticipated sharp hydraulic and thermal gradients. Those mesh resolutions result in a total amount of 1 326 254 finite elements in the reference model, while the karst model in accordance with the shorter well section consists of 560 431 tetrahedral elements.

We impose a hydrostatic and a conductive gradient as initial conditions (ICs) for the primary variables pressure p_f and temperature T, respectively. Along the vertical model boundaries, a hydrostatic pressure gradient is set with a constant Dirichlet BC (Fig. 1). With an estimated maximum temperature gradient of 36 °C km⁻¹, a constant temperature (i.e. Dirichlet BC) equal to 82 °C is considered at top of the model domain, whereas at bottom a constant terrestrial heat flow of 110 mW m⁻² (i.e. Neumann BC) is defined. The fluid injection temperature in the two wells is imposed with a Dirichlet BC, whereas the flow rates are applied as transient mass flux functions. Both, injection temperature and flow fluxes are assigned 40 m below the top reservoir (i.e. at −1840 m a.m.s.l.) to avoid interference effects by implementing them directly on the reservoir–confining unit interface.

2.4 Performance evaluation

A commonly adopted parameter utilized in the evaluation of ATES systems operation is the fraction of recovered thermal energy in relation to the energy injected. A proportion of the injected thermal energy is not recovered due to arising heat losses either by temperature equilibration between the injected fluid volume and the rock matrix, or by conductive and convective heat transfer. The heat recovery factor (η) is considered as an indicator to estimate thermal losses, describing thus the thermal performance of the HT-ATES system. It is defined as the ratio between the recovered to the injected thermal energy and is estimated by the following expression:

$$\begin{array}{}\text{(4)}& \mathit{\eta }={\displaystyle \frac{\underset{t_{\mathrm{discharg},\mathrm{start}}}{\overset{t_{\mathrm{discharg},\mathrm{end}}}{\int }}\dot{m}{c}_{p,\mathrm{f}}\left(T_{\mathrm{prod},\mathrm{warm}}\left(t\right)-T_{\mathrm{inj},\mathrm{cold}}\left(t\right)\right)\mathrm{d}t}{\underset{t_{\mathrm{charg},\mathrm{start}}}{\overset{t_{\mathrm{charg},\mathrm{end}}}{\int }}\dot{m}{c}_{p,\mathrm{f}}\left(T_{\mathrm{inj},\mathrm{warm}}\left(t\right)-T_{\mathrm{prod},\mathrm{cold}}\left(t\right)\right)\mathrm{d}t}},\end{array}$$

where $\dot{m}$ is the mass flow rate, c_p,f the specific heat capacity of the fluid, T_prod(t) and T_inj(t) the time-varying temperature of the produced and injected fluid volume, respectively, in the warm and cold well denoted by the respective subscript, while t_{discharg,start}, t_charg,start and t_discharg,end, t_charg,end indicate the initiation and end of the discharging and charging periods, respectively.

Another key performance factor denoting the efficiency of fluid injection into and production from the reservoir through a well is the injectivity (II) and productivity (PI) index. Those indexes are indicators of the well performance during operation. Analysis of the two indexes is of great significance, contributing towards optimization of the operation process and towards proper management of the reservoir performance. The general form of the productivity and injectivity indexes is:

$$\begin{array}{}\text{(5)}& \mathrm{PI}/\mathrm{II}={\displaystyle \frac{\dot{V}}{\mathrm{\Delta }{p}_{\mathrm{f}}}},\end{array}$$

where $\dot{V}$ is the volumetric flow rate, and Δp_f denotes the pressure differential between the initial undisturbed pressure and the pressure at the end of each operation phase.

3 Computation results

3.1 Thermal field and heat recovery factor

Computation results capture the thermal front propagation that develops initially in the rock volume adjacent to the wells and gradually progresses radially into the reservoir rock matrix. Figure 2a depicts the simulated temperature field of the reference model reflecting the thermal perturbation in the vicinity of the warm well at the end of the last charging phase, after 9.5 years of simulation. Results demonstrate a non-uniform layer-specific distribution of the thermal front propagation in the vertical direction. This system response is due to the stratification of the reservoir with associated unit-specific distinct permeabilities, and the consequent spatial variation in the imposed hydraulic gradients that induce more vigorous advective fluid and heat flow primarily into the high-permeability layer. In coherence, fluid and heat transfer in the deeper lower-permeability units is considerably decreased and spatially confined in the direct proximity of the warm well.

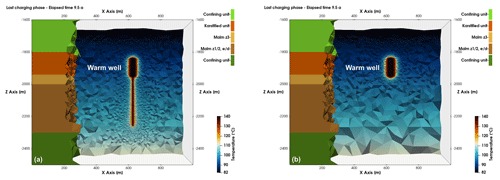
Figure 2 Computed temperature profile in the proximity of the warm wellbore for the (a) reference and (b) karst model at the end of the last charging period, after 9.5 years of simulation. Modelled units are illustrated for comparison.

Deriving from the inferred anisotropic spatial distribution of the thermal front propagation, in the subsequent karst model scenario injection only in the principal hydraulically-conductive unit is investigated serving towards comparison of the two system configurations. In the karst model, the thermal front is limited to the upper reservoir section (Fig. 2b), that is in the reservoir horizon where active injection is performed. This simulation aims at quantifying the impact on the recovered fluid-temperature, and thus on the recovery efficiency if omitting fluid injection into the lower-permeability layers where, in the reference model, heat propagation is diminished (Fig. 2a). This is due to the geometrical shape of the thermally perturbed rock volume since heat losses arise during thermal equilibration between injected fluid and reservoir rock, as well as at the interface between propagating thermal front and adjacent rock matrix. Our numerical results reveal that the thermally influenced rock volume, here defined as an injection-induced increase in reservoir temperature higher than 110 °C, in the reference model is 839 993 m³, whereas the respective of the karst model equals 673 367 m³. The thermal-perturbation radius extends approx. 4 m deeper into the reservoir in the karst model as the same fluid volume is injected in a single layer (Fig. 2b).

In both simulations, density-driven buoyancy, which could considerably decrease thermal efficiencies is impeded, and thus the prevailing heat transport mechanism is forced convection. This system response is attributed to the high operation fluid fluxes that promote steep lateral hydraulic gradients suppressing the onset of destabilizing buoyant forces. In parallel, the relatively low reservoir permeability builds synergies towards the absence of any influential convective patterns.

In Fig. 3 we cross-plot the temperature evolution in the warm and cold well at −1840 m a.m.s.l. for both models over the entire 10 years of simulation time. In both models the fluid temperature in the warm well increases per operation cycle over the successive production phases. This rise is driven by an equivalent gradual temperature improvement in the reservoir itself, induced by thermal equilibration between the injected fluid and the reservoir during each charging phase, which in turn enhances the residual heat in the reservoir at the end of each consecutive discharge period. Nevertheless, we also note that recovered fluid temperatures are higher in the karst model. Those results imply that injection into the two deeper layers likely enhances heat losses from the injected fluid volume to the reservoir rock matrix, and thus deteriorates the HT-ATES system thermal performance.

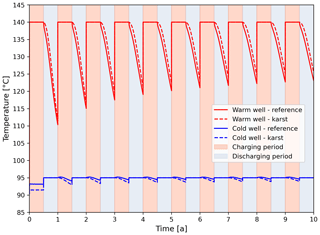
Figure 3 Simulated temperature development in the warm and cold wellbore at −1840 m a.m.s.l. of the two simulated models over the complete simulation time. Red and blue shaded areas highlight the consecutive reservoir charging and discharging periods, respectively.

Fluid temperature in the cold wellbore experiences lower magnitude fluctuations over the simulation since fluids are injected with the average reservoir temperature. Composed of a fluid mixture from different depths, the temperature in the reference model rises from 90.3 to 93 °C during the first production phase. This temperature increase is lower in the karst model (91.5 °C) since the produced fluid mixture originates only from the shallower reservoir section. The subsequent fluid injection with 95 °C and the observed positive step in temperature correlates with the depth of the selected plotting point, i.e. –1840 m a.m.s.l. Per increase of reservoir temperature at deeper reservoir segments, this positive step is expected to attenuate.

We utilize the numerical results to estimate the anticipated thermal recovery factor (η) for the two systems. The recovery factor increase per year of operation observed in both case studies is in agreement with the progressive improvement in the temperature of the produced fluid volume. Besides, this increase is sharper in the first years of operation, whereas the rate of increase levels off gradually over the simulation. Results confirm that the derived factors are higher in the karst model. Inferred values in the reference model vary between approx. 0.65 in the first year and 0.82 in the last year of operation, while those of the karst model range from approx. 0.68 to 0.87, respectively.

The interplay of two principal heat transfer mechanisms induces thermal energy losses, and thus triggers the observed time-varying behaviour of temperature and heat recovery. The first process is related to the portion of rock volume for which injected fluid and host rock have to reach to a thermal equilibrium. In the presented simulations, since identical operation parameters are assigned, this transport process is only a function of the thermally influenced rock volume. Apart from this, conductive heat losses are reinforced at the contact-surface area between propagating thermal front and adjacent rock matrix. Doughty et al. (1982) showed that the conductive heat loss rate from a thermally perturbed rock volume to the neighbouring matrix is proportional to its surface area to volume. Initially, as the system is characterized by a high temperature differential between injected fluid and rock matrix, the first triggering mechanism of heat loss prevails. However, over time as the reservoir is conditioned, conductive heat losses gain progressively in significance.

The two described heat transfer mechanisms causing thermal energy loss are active in both simulated systems. However, the higher portion of the thermally perturbed rock volume in combination with an enhanced ratio of surface area to volume (Doughty et al., 1982) in the reference model explain the inferred differences in the fluid temperature and estimated heat recovery factor between the two models.

3.2 Pressure evolution and productivity/injectivity index

The simulated pressure development in the warm (Fig. 4a) and cold (Fig. 4b) well at −1840 m a.m.s.l. for both models reflects an immediate pressure response of the system upon injection and production. During the fluid injection phase, the pressure build-up is higher in both wells in the case of the karst model, while, in turn, during fluid production, this model is characterized by steeper pressure drawdown in both wells. This system response is ascribed to the lower transmissibility of the karst model stemming from the shorter section of hydraulic connection between the well and the reservoir. We further notice that the pressure in both wells decreases during a single injection cycle, and that this decline is more pronounced for the karst model. Those observations point to the influence that the considered density and viscosity variation exerts on the developing physical processes and resulting well performance. These implications are not detailed here, and a comprehensive analysis will be incorporated in a subsequent manuscript.

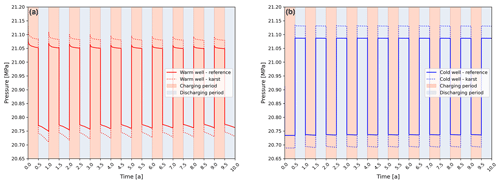
Figure 4 Simulated pressure evolution in the (a) warm and (b) cold wellbore at −1840 m a.m.s.l. of the two models over the entire simulation time. Red and blue shaded areas mark the consecutive reservoir charging and discharging phases, respectively.

Table 3 Inferred ranges of productivity and injectivity index of both wells for the reference and karst model scenarios.

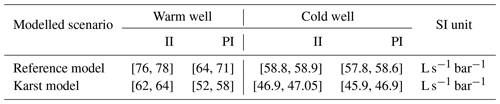
Influenced by the combined effect of the variation in the pressure differential and in the volumetric flow rate, the productivity (PI) and injectivity (II) indexes are subjected to a time-varying behaviour. We observe that all indexes manifest an increasing trend over the simulation time, whereas in both models the warm well is characterized by higher PI and II values when compared to those of the cold well. In parallel, for both wells the II is higher compared to the PI. Those implications derive from the temperature evolution in the system, superimposed by the integration of density and viscosity effects which induce a fluctuation in the pressure differential and volumetric fluxes. As stated before, the underlying physical processes will be presented in more detail in an upcoming work. To provide an overview of the deciphered conclusions described in this paragraph, the ranges of the PI and II values of the simulated scenarios are presented in Table 3.

4 Conclusions

In the present work a coupled thermal-hydraulic numerical analysis constrained by the encountered Upper Jurassic reservoir rock properties and a feasible operation scheme is performed to assess HT-ATES application in the German Molasse Basin. Two HT-ATES-system configurations are examined, differentiated by the extent of the well-screen into the Upper Jurassic geothermal reservoir, and the spatial and temporal physical state distribution for both systems is derived. Results indicate dominance of advective-dominated flow imposed by the steep lateral hydraulic gradients due to the elevated flow rates. The principal conductive and convective driving mechanisms impacting the storage of thermal energy into the reservoir rock matrix are further addressed. The simulations reveal the relative contribution of these components, and their temporally transient significance into the loss of thermal energy from the injected fluid volume to the host rock. Implications from the incorporation of density and viscosity variation in the performance of the wells are additionally inferred, consequently pointing to their indispensable numerical consideration towards proper prediction of the computed state field of the problem.

In terms of HT-ATES application in the Upper Jurassic reservoir, the numerical computations predict promising heat recovery efficiencies in both HT-ATES-system configurations. In specific, results suggest that under the investigated stratified reservoir setting, fluid injection into the deeper lower-permeability zones acts towards advancing thermal energy losses. This system response is driven by the higher portion of the thermally influenced rock volume in conjunction with an enhanced ratio of the developing surface-area of the propagating thermal front to the thermally perturbed rock volume. It is therefore concluded that under the specified stratified reservoir configuration constrained additionally by the selected spatial distribution of rock properties, heat storage performed only into the upper high-permeability zone corresponds to an improved thermal performance.