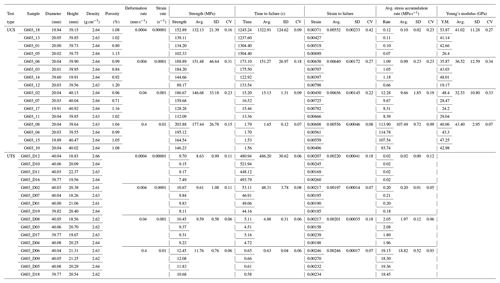
Rate-dependence of the compressive and tensile strength of granites

The strength and rupture of geomaterials are integral to subsurface engineering practices, such as those required to optimise geothermal energy extraction. Of particular importance is the time- and strain-rate-dependence of material strength, which dictates the energy released upon failure, and impacts the magnitude of induced seismicity, fracture architecture and thus hydraulic conductivity and system permeability. Here, we performed a series of uniaxial compression and Brazilian tensile strength measurements at a range of deformation rates in order to constrain the impact of strain rate on the strength of G603 granite. The dense, low permeability, medium-grained granites were mechanically tested at 4 strain rates (or diametric equivalent strain rates in the case of Brazilian tests) from 10⁻⁵ to 10⁻² s⁻¹, such that sample failure was achieved in anything from below 1s at the fastest rate in tension, to over 1000s at the slowest rate in compression. The applied rates encompassed those recommended by ISRM and ASTM material testing standards for compressive and Brazilian tensile testing. We found a significant rate strengthening effect, whereby compressive and tensile strength both increased by approximately 35 % across the 4 orders of magnitude of strain rate tested. We found that the static Young's modulus remained relatively constant across this range of deformation rates, however variability was reduced at faster rates, owing to the reduced time for equilibration of the system to imposed stresses. The lower strength at slower strain rates causes smaller stress drops, indicating that rocks driven to compressive and tensile failure at slower rates release less energy upon failure. Such constraints of the strain-rate-dependence of material strength, in contrast to the use of standardised material characteristics conventionally used in Engineering Geology applications, will prove useful as we develop increasingly sophisticated strategies such as cyclic soft stimulation to access resources using less energy, whilst reducing environmental risk and producing less waste.

1 Introduction

An understanding of the strength of geomaterials is vital for many geological and man-made phenomena, such as earthquakes, volcanic eruptions, landslides, dams, mine bursts and hydraulic fractures during subsurface resource extraction. In the upper crust, brittle fractures dominate and span all scales. Even crustal-scale events must originate on initial microfractures (at mineral/grain scale) which nucleate, grow and coalesce (Paterson and Wong, 2005) at increasing scale until the accumulated energy is spent (Brantut et al., 2014). For almost a century, laboratory derivation of material properties have focused on constraining rock mechanical parameters at standard conditions to draw comparisons between materials, to link mechanical and petrophysical characteristics and to develop engineering guidelines (ASTM, 2014, 2008; ISRM, 1978; Bieniawski and Bernede, 1979). Standardised deformation rates and test durations have frequently been employed that represent a point at which rock behaviour has been approximated as time-independent (Paterson and Wong, 2005); in this context time-independence refers to the ability for a constant fracture toughness value or stress intensity to explain critical crack growth (for a detailed discussion see Brantut et al., 2014). In the last decades, increasingly sophisticated machines and sensors to test these properties, enhanced data handling capabilities for complex datasets, and the wealth of standardised strength data already collected, have allowed us to push the boundaries of our description of geomaterial strength to encompass new stress field geometries and faster, more dynamic conditions (Alatorre-Ibargüengoitia et al., 2010; Gong et al., 2019b; Heap et al., 2011; Hirose and Shimamoto, 2005; Zhuang and Zang, 2021). Such constraints are vitally needed in order for the inherent time- and rate-dependent character of rocks to be incorporated to our description of their strength (Dusseault and Fordham, 1993; Das and Scholz, 1981; Dieterich, 1972; Rutter, 1986). Moreover, these new descriptions are necessary in the face of ongoing demand for, and increasing scarcity of, resources in the Earth's crust, as we develop new strategies to manipulate geomaterials to yield assets at higher efficiency whilst minimising risk. In this paper we explore the impact of strain rate on the strength of a dense, medium-grained granite in both compression and tension (unconfined uniaxial compressive strength and Brazilian disc tensile strength tests) across 4 orders of magnitude of strain rate.

2 Method

2.1 Sample preparation

A medium-grained Chinese G603 granite, a standard granite utilised frequently in construction, was used for this study. Cylinders of 20 and 40 mm diameter were cored from a large block using a pillar drill. The 20 mm diameter cylinders were cut and ground to produce cores of 40 mm length, whilst the 40 mm diameter cylinders were cut and ground to discs of 20 mm length (Fig. 1). Cores were subsequently used for density and porosity measurements, and for uniaxial compressive strength tests. Discs were used for density measurements and for Brazilian tensile strength measurements. Samples were dried for 48 h at 60 ^∘C and stored in a desiccator until utilised for testing.

Figure 1 Photographs of a representative core for porosity measurements and uniaxial compressive strength testing, and a disc for Brazilian tensile strength testing. Phenocrysts of feldspar (pale pink), with finer grains of quartz and plagioclase (both white to pale grey) and clusters of mica (dark grey to black) are visible.

2.2 Density and porosity

For the 36 cores and discs of granite, the mass (m; in grams), sample length (l; in centimetres), diameter (d; in centimetres) and thus radius (r; in centimetres) were recorded, providing sample density (ρ_s; in grams per cubic centimetre) via:

$$\begin{array}{}\text{(1)}& {\mathit{\rho }}_{\mathrm{s}}={\displaystyle \frac{m}{\mathit{\pi }{r}^{\mathrm{2}}l}}\end{array}$$

The porosity was determined for the 18 core samples using an AccuPyc 1340 helium pycnometer from Micromeritics. The material volume was measured (V_m; in cubic centimetres) for each core in a 35 cm³ cell (with volume accurate to ±0.1 %). The connected porosity (∅_c) of the samples was then determined via:

$$\begin{array}{}\text{(2)}& {\mathrm{\varnothing }}_{\mathrm{c}}=\mathrm{1}-{\displaystyle \frac{V_{\mathrm{m}}}{\mathit{\pi }{r}^{\mathrm{2}}l}}\end{array}$$

2.3 Mechanical testing

2.3.1 Uniaxial compressive strength

16 cores were assigned to uniaxial compressive strength (UCS) tests at 4 different strain rates (4 per rate). UCS tests were performed on a 100 kN Instron 8862 uniaxial press with FastTrack 8800 tower and Instron Dynacell 2527 load cell. The strain rates used for testing were 10⁻⁵, 10⁻⁴, 10⁻³ and 10⁻² s⁻¹, equivalent to deformation rates of 0.0004, 0.004, 0.04 and 0.4 mm s⁻¹ respectively. Load and axial displacement were logged, and compressive stress and strain (ε) were calculated and recorded in real-time during deformation at a rate of 10 to 1000 Hz (depending on the deformation rate). All mechanical data were corrected for the compliance of the loading assembly. The specimen dimensions and applied rate of 10⁻⁵ s⁻¹ follows the ASTM (D7012) standard for UCS testing (ASTM, 2014). UCS was defined as the peak stress prior to rupture, and the end of each experiment was defined by a stress drop exceeding 25 % of the peak stress. Young's modulus was calculated from a segment of the linear elastic portion of the stress strain curve, picked using an automated Matlab script (following Lamur et al., 2023). The code runs a long window (totalling at least 20 % of the loading data) through the stress-strain curve as well as 5 smaller windows (within the longer one) to calculate the local linear regression using the least square method in every window. The code then finds the minimal ratio between the results of the 5 short-term regressions over the long-term regression to automatically pick the most linear portion of the curve and estimate the Young's modulus as the slope of the long-term window (see Supplement).

2.3.2 Brazilian disc tensile strength

16 discs were assigned to Brazilian disc tensile strength (UTS) tests at 4 different rates (4 per rate). The same uniaxial press and approach was utilised as in the UCS tests, and in this case we refer to the diametric equivalent strain rate due to the sample geometry of a diametrically compressed disc in a flat plate loading geometry (Gong et al., 2019a). Load (N) and axial displacement were logged, and diametric equivalent strain was calculated throughout the tests. Tensile stress (σ_t) was calculated and recorded in real time via:

$$\begin{array}{}\text{(3)}& {\mathit{\sigma }}_{\mathrm{t}}={\displaystyle \frac{\mathrm{2}N}{\mathit{\pi }dl}}\end{array}$$

where d is diameter and l is the length of the disc (ISRM, 1978). UTS was defined as the highest recorded stress prior to sample rupture and tests were stopped automatically following a stress drop exceeding 25 % of the peak stress. Recommended methods and standards given for Brazilian disc testing are not always consistent in terms of defined deformation or loading rate and/or time to failure (Li and Wong, 2013; Hornby et al., 2019), but at 10⁻³ to 10⁻⁴ s⁻¹ tested here we encompassed the values recommended by both ASTM (D3967) and ISRM (ISRM, 1978; ASTM, 2008).

3 Results and Discussion

3.1 Density and porosity

The 36 samples measured had a density of 2.63 g cm⁻¹ (±0.02) with a standard deviation of 0.01. The 16 samples measured for porosity had an average of 1.00 % (±0.29) with a standard deviation of 0.13 (Table 1). Porosity in granites is typically dominated by grain boundaries and microcracks in minerals (e.g. Vollbrecht et al., 1991; Schild et al., 2001). In these samples, variability in porosity is probably related to the constituent phases present; the samples contain relatively large and heterogeneously distributed phenocrysts of feldspar (typically on the order of 1–2 mm, but occasionally >8 mm; in the cases where phenocrysts exceeded 2 mm in the cored rock the samples were not used), with finer grains of quartz and plagioclase (typically 0.5–1.5 mm) and clusters of mica (individually <0.5 mm). As the constituent phases vary slightly from sample to sample there is also a slight dichotomy in the correlation between porosity and density (one does not necessarily change in parity with the other; Table 1).

Table 1 Sample geometry, test conditions and mechanical results for all experiments, including calculated averages (Avg.), standard deviation (SD) and coefficient of variation (CV).

3.2 Mechanical Testing

We found that the granites tested were rate strengthening in both compression and tension (Table 1), across the 4 different strain rates, or diametric equivalent strain rates, tested. The suite of UCS and UTS tests on the granite showed a degree of variability at each tested condition (Fig. 2), particularly in terms of the amount of inelastic compaction (the initial non-linear portion of the stress-strain curve) experienced at the onset of loading (e.g. Fig. 2a in compression, and Fig. 2b in tension). The main contribution to inelastic compaction at the onset of loading is the closure of microfractures sub-perpendicular to the principal applied stress (Renard et al., 2019; Scholz, 1968). Therefore, we attribute the differences in inelastic compaction to the sample-to-sample variability in the distribution of the mineral phases and porosity. Following the initial inelastic compaction, the elastic portion of the stress-strain curves typically more closely resemble one another within a given experimental condition, though occasional outliers show higher or lower slopes (Fig. 2). We can also attribute these outliers to sample-to-sample differences in constituent minerals, since each mineral phase has contrasting elastic properties (Healy et al., 2020). Finally, the peak stress achieved, and thus the strength of the granites in the UCS and UTS tests at a given condition also show some variability, notably there are occasional weaker outliers (e.g. G603_5 in Fig. 2a and G603_12 in Fig. 2c) but more rare stronger outliers (e.g. G603_02 in Fig. 2e). The weaker outliers are likely a result of more dominant microfractures, as indicated by their higher-than-average porosities (Table 1). Although samples with visible phenocrysts exceeding 1:10 ratio of sample dimensions (i.e. 2 mm) were excluded, we cannot rule out the presence of large feldspar phenocrysts internally, which could also contribute to lower strengths since feldspars are typically relatively weak, and since the strength of igneous rocks is known to be inversely proportional to grain size (Du et al., 2022). A lower abundance of larger feldspar phenocrysts in a given sample could be responsible for occasional higher strength outliers (e.g. Fig. 2e).

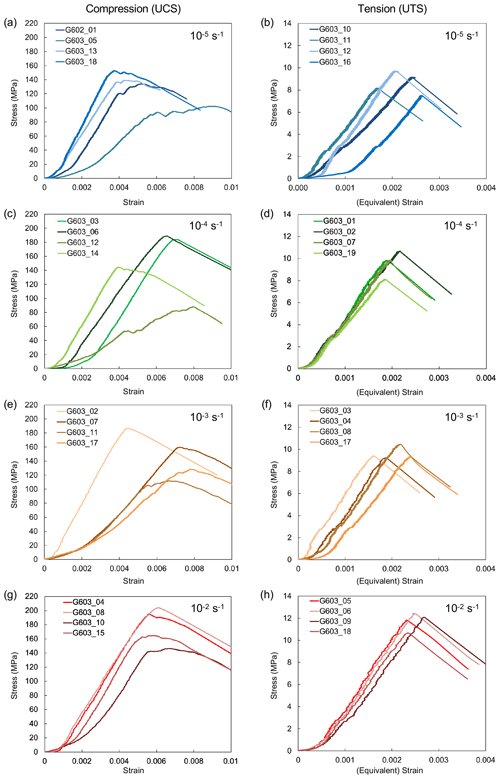
Figure 2 Stress-strain curves for uniaxial compressive strength (UCS; left) and Brazilian tensile strength (UTS; right) tests at strain rates of (a)–(b) 10⁻⁵ s⁻¹, (c)–(d) 10⁻⁴ s⁻¹, (e)–(f) 10⁻³ s⁻¹ and (g)–(h) 10⁻² s⁻¹. Four tests were made at each condition, see Table 1 for details.

Despite these variations within the individual test conditions, clear trends can be identified between the mechanical properties as a function of the applied strain rate (Fig. 3; Table 1). Specifically, the compressive strength increased from 132.1 MPa at the slowest strain rate of 10⁻⁵ s⁻¹ to 177.4 MPa at the fastest strain rate of 10⁻² s⁻¹, an increase of just over 34 % (Fig. 2a). Comparably, the Brazilian tensile strength ranged from 8.6 MPa at the slowest rate, to 11.8 MPa at the fastest rate, an increase of just over 36 % (Fig. 2b). A ratio of 15:1 UCS:UTS was consistently observed for the average strength across all rates tested (with standard deviation of 0.28).

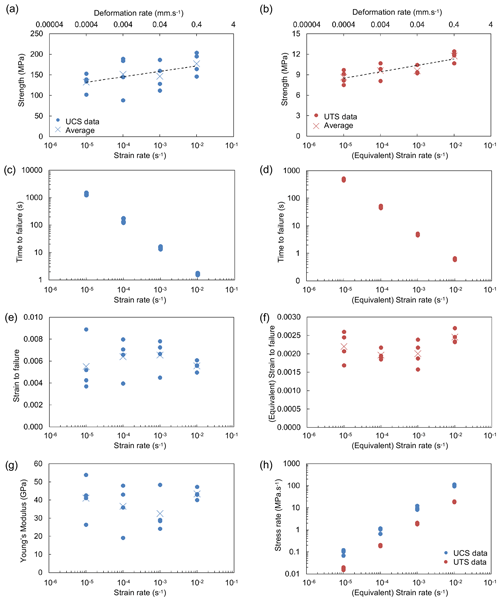
Figure 3 Summary mechanical data: Increasing (a) Uniaxial compressive strength (UCS) and (b) Brazilian tensile strength (UTS) as a function of applied strain rate. Reducing time to failure for (c) UCS and (d) UTS as a function of applied strain rate. Strain to failure for (e) UCS and (f) UTS is unchanged as a function of applied strain rate. (g) Young's modulus is stable, but variability reduces as a function of applied strain rate. (h) The average rate at which stress accumulates is higher in UCS than UTS at the same strain rate.

The time taken to induce failure was significantly faster in tension than in compression owing to the lower tensile strength, and under each deformation rate was highly consistent in both compression and tension, following an inverse linear trend with applied strain rate (Fig. 3c–d; Table 1). The average strain to induce failure was consistently 2–3 times higher in compression than in tension, and in both UCS and UTS did not show systematic variation with applied strain rate, with the average remaining relatively consistent across the strain rates tested. We noted a slight reduction in the variability of the strain to failure at faster rates in both regimes (Fig. 3e–f; Table 1). The Young's modulus, calculated from the linear portion of the stress-strain pathways of the samples in compression (see Supplementary information for the areas used to calculate Young's modulus in each test), is an important parameter for modelling stress-strain response of materials to different loading pathways. We found Young's modulus to be rate independent, though similarly to the strain to failure values we observed a reduction of the spread of values at faster rate (Fig. 3g). That this linear portion of the stress-strain curves should remain unchanged as a function of strain rate is intuitive given it represents the accumulation of recoverable elastic strain during loading.

The observations made in this experimental study permit an assessment of the role of strain (or manipulation) rate on the mechanical properties of rocks in engineering practices. The increased strength, and the reduced scatter in Young's Modulus and strain to failure at faster rates may be attributed to the fact that at faster deformation or strain rates, there is reduced time for heterogeneities to develop in the materials, for example via coalescence of fractures. At higher rates rupture strength is therefore more of a depiction of the strength of the solid constituents of the sample, and less reliant on the initiation, propagation (from new and existing microfractures) and coalescence of cracks (Ashby and Sammis, 1990) and thus the sample-to sample variability is also effectively reduced compared to slower rates of deformation. In turn, this implies that it is the time dependence of composite materials, including rocks (e.g. Brantut et al., 2013), which causes weakening at slower deformation rates, and that this process is also active across the range tested here (Fig. 3). Though it has been previously asserted that rocks are essentially time-independent under typical experimental rates since critical crack growth can be attributed to constant fracture toughness (e.g. Paterson and Wong, 2005). At slower deformation rates, or under creep conditions relevant to most geological timescales, subcritical crack growth is invoked to explain the reduction in failure stress and the deficit in energy required to induce failure of materials (Brantut et al., 2014; Ashby and Sammis, 1990; Brantut et al., 2012). Across the range tested here, we must invoke a weakening mechanism at slower rates, or strengthening at faster rate. Interestingly, our study demonstrates an equivalent rate strengthening behaviour under tension (as well as compression) at these rates, which have been relatively underexplored to date (Hornby et al., 2019; Gong et al., 2019a), but which are vitally important in shallow geological phenomena such as volcanic eruptions and landslides, and man-made activities such as tunnelling and hydraulic fracturing. Compressive and tensile strength increased similarly with rate (the UCS:UTS ratio remained fixed at approximately 15:1), which suggests a commonality in the cause in both regimes, namely, the time dependence of crack opening, which in low- or un-confined compression also typically occurs as Mode-I tensile fractures (Diederichs et al., 2004; Li et al., 2017); N.B. at later stages of crack growth the mechanisms in compression and tension diverge (Ashby and Sammis, 1990). At faster rates, this opening may lag behind applied strain due to an effect such as the material-specific incubation time (Petrov et al., 2012) which is invoked in dynamic testing (typically at rates exceeding 10¹ s⁻¹) as it facilitates more stress to accumulate before wholesale failure (e.g. Xu et al., 2023). However, work is needed to understand the relationship between compressive and tensile strength which is often assumed to be approximately 10:1 but which has been shown be highly variable in different materials, to vary as function of porosity even within a given rock type, to be sensitive to macroscopic material properties, and to vary across scales (Perras and Diederichs, 2014; Nazir et al., 2013; Lavallée and Kendrick, 2021); thus it is likely that the rate-strengthening behaviour in compression and tension of some materials may diverge and therefore that a broad spectrum of materials may need appraisal in different regimes at a range of rates to develop a complete picture.

Anthropogenic activities have increasingly pushed the rates of deformation (up to m's per second; c.f. Renshaw and Harvey, 1994) we need to consider to fully understand the behaviour of the subsurface, including during stimulation practices and extraction of resources. Many unforeseen and hazardous side-effects such as rock-bursts in mines (Wang and Kaunda, 2019), contamination of water supplies (Jackson, 2014), or induced seismicity (Ma et al., 2020) result from the failure of rocks (or other composites such as cements), highlighting the need for a better understanding of the rate-dependence and time-dependence of rock strength across a broader spectrum of conditions, including rapid and dynamic testing (e.g. Gong et al., 2019b). A better understanding of this time- and rate-dependence does however provide opportunities to safely introduce novel strategies to extract subsurface resources at higher efficiency. For example, knowledge gleaned from experimental testing indicates cyclic soft stimulation practices (Hofmann et al., 2018) are likely to effectively enhance fluid conductivity of geomaterials through progressive dilation (c.f. Scholz and Koczynski, 1979) and may facilitate more controlled fracture growth that could minimise large induced seismic events that currently hamper subsurface operations, as the energy is consumed by more numerous small events (c.f. Ojala et al., 2004). In a complementary study, Alneasan et al. (2022) found that slower strain rates induced wider fractures at lower breakdown pressures, thus targeted, material-specific and responsive stimulation practices present an opportunity for future resource extraction endeavours.

4 Conclusions

The dense, medium-grained granites tested here displayed equivalent rate strengthening in both compression and tension. Unconfined uniaxial compressive strength and Brazilian disc tensile strength tests showed an increase in average strength of 34 % and 36 % respectively across four orders of magnitude of strain rate (or diametric equivalent strain rates in the case of Brazilian tests) from 10⁻⁵ to 10⁻² s⁻¹. The results indicate that time-dependent behaviour of these dense rocks is important at these rates, which encompass those recommended by ISRM and ASTM material testing standards for compressive and Brazilian tensile testing. We found that the strain needed to induce failure and the static Young's modulus remained relatively constant across this range of deformation rates, however variability was reduced at faster rates with less time for equilibration of the system to imposed stresses. Failure induced at lower strain rates under compression and tension had lower stress drops, indicating a lower energy consumption of the failure events at slower rates. In combination with previous assertions that less mechanical work is consumed by failure at slow rate (Brantut et al., 2014), and that dilation is enhanced by stress cycling (Scholz and Koczynski, 1979) our observations show promise for the development of subsurface engineering strategies for resource extraction that exploit the time-dependent characteristics of rocks, such as cyclic soft stimulation. Moreover, an accurate constraint of material properties at conditions appropriate to engineered subsurface activities will be vital to minimise waste production and environmental risks which are under increasing scrutiny as we target a net-zero future.