Neapolitan volcanic area Tide Gauge Network (Southern Italy): Ground Displacements and Sea-Level Oscillations

In this study, we investigate the oscillations of relative sea level through the analysis of tide gauge records about 10-year long collected in the Gulfs of Pozzuoli and Napoli (Southern Italy). The main goal of this study is to provide a suitable resolution model of the sea tides including low frequency (seiches), tidal bands and non-linear tides. The spectral analyses of the tide gauge records lead us to identify a number of seiche periods some of them already known from the literature and some other unknown. Furthermore, we target a non-conventional purpose of the tidal analysis, namely extracting from the tide gauge records the volcano-tectonic signal (vertical ground displacement) in the resurgent Campi Flegrei caldera. We suggest a method to filter out the volcano-tectonic signal (bradyseism) from the tide gauge records by deconvolving it from two records, one collected in the active volcanic area (Pozzuoli) and the other one collected in a tectonically stable station (Napoli), located beyond the caldera rim. Finally, we retrieve the relative mean sea level change in the Gulf of Naples and compare it with the trend found in five tide gauges spread along the Italian coast.

1 Introduction

Neapolitan volcanic district is among the areas with the highest volcanic risk due to the intense urbanization. Two volcanoes, Somma-Vesuvius and Campi Flegrei caldera, overlook the Gulfs of Napoli and Pozzuoli (southern Italy), respectively.

Somma-Vesuvius is a strato-volcano located east of Naples. It is composed of an older edifice Mt. Somma truncated by a summit caldera, and a more recent cone, called Vesuvius, grown within the caldera. It covers an area of 165 km² (Principe et al., 1987). Nearly 600 thousand people live on its slopes and surroundings. Therefore, Somma-Vesuvius may be considered a relatively small volcano with an associated high level of risk (Auger et al., 2001). Since the last eruption, occurred in March 1944, the Somma-Vesuvius volcano is in a quiescent phase. Hundreds of low energy earthquakes per year, land subsidence (Pingue et al., 2013; Tammaro et al., 2013) and low temperature fumaroles characterize its activity. The largest earthquake (M_d=3.6) was recorded in October 1999 (Del Pezzo et al., 2004; De Natale et al., 2004; Galluzzo et al., 2004; Cubellis et al., 2007). Campi Flegrei caldera (CFc) consists of a continental and submerged part. It formed during two major caldera collapses related to the eruptions of the Campanian Ignimbrite (39 ka, Fedele et al., 2003; Marianelli et al., 2006) and the Neapolitan Yellow Tuff (15 ka, Deino et al., 2004), respectively (Orsi et al., 1996). The CFc last eruption, occurred in 1538, and gave rise to Mt. Nuovo. With more than 300 000 people living within the caldera, the volcanic risk at CF is considered to be substantial (Bevilacqua et al., 2015). CFc is one of the most interesting examples of resurgent caldera, it is renowned worldwide for bradyseism phenomenon (literally “slow seism”, from Greek), a slow ground uplift/subsidence movement which characterises the dynamics of several volcanic areas and was firstly recognised and studied at this caldera (e.g. Amoruso et al., 2014; Capuano et al., 2013; De Martino et al., 2014; Macedonio et al., 2014; Petrillo et al., 2013; Romano et al., 2012, 2018; Trasatti et al., 2015; Troise et al., 2019). In recent times CFc has been affected by intense episodes of uplift (Barberi et al., 1984; Rosi and Sbrana, 1987; Isaia et al., 2009). The last two largest uplift episodes occurred from 1969 to 1972 and from mid-1982 to December 1984 with net uplifts, in the Pozzuoli town, of about 1.7 and 1.8 m respectively (Corrado et al., 1977; Berrino et al., 1984; Luongo et al., 1991; Berrino, 1998). During 1982–1984 uplift episode more than 15 000 earthquake occurred with magnitude between 0.4 and 4.2.

In March 1970, during the bradyseismic crisis of 1969–1972, the first systematic observation of the sea level in the Gulf of Pozzuoli began with the aim of assessing the vertical movements of the ground. Four stations were installed, constituting the starting point of the current Neapolitan Tide Gauge Network (NTGN), operated by Osservatorio Vesuviano (OV), which is a branch of the Istituto Nazionale di Geofisica e Vulcanologia (INGV).

The main goal of this paper, beyond the study of the ground displacements, is to characterize the tidal response of the two basins, Gulf of Napoli and Gulf of Pozzuoli, through a spectral analysis of the tide gauge records to extract both the main tidal components and seiches at each station of the network. Moreover, despite the shortness of the available time series, the relative mean sea level in both the Gulfs is eventually estimated.

The paper is organized as follows. The Sect. 2 illustrates the evolution of the Neapolitan Tide Gauge network, since its birth up to now. In Sect. 3, we briefly describe the data set and the data analysis method. Section 4 shows harmonic tidal and non-tidal analysis. Section 5 reports on the attempt to retrieve the volcano tectonic signal from the tide gauge record, while Sect. 6 deals with the assessment of the relative mean sea level change. The Sect. 7 contains the conclusions.

2 Neapolitan Tide Gauge Network

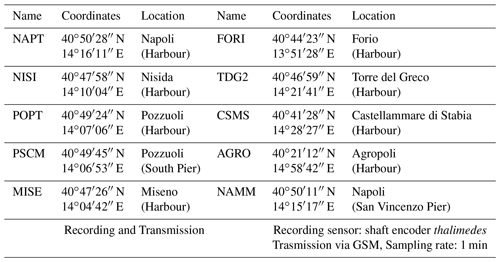
In March 1970, in the Gulf of Pozzuoli, a permanent tide gauge (TG) network consisting of four stations (Miseno, Pozzuoli harbour, Pozzuoli Ansaldo and Nisida) was set up (Corrado et al., 1977), “as part of the geophysical surveillance system promoted by Ministry of Public works and Italian National Research Council” (Corrado and Luongo, 1981). The Tide Gauge Network was completely modernised starting from 2002, when the gauges were converted from analogue to digital with automatic and remote data transfer to the observatory acquisition centre. Until then the tide gauge stations were equipped with mechanical sensors based on a floating body system and a local recording on a hardcopy helicorder. Starting in October 2002, a completely new digital gauge sensor and data taker system was installed in all the sites. This system (sampling rate ranging 1–5 min) is able to allow a local data management and a quasi-real time GSM transmission to the acquisition centre located at Osservatorio Vesuviano headquarter. The headquarter assures the display of the collected data, checking for the functionality of the acquisition systems and a first and draft data analysis. The quality control relies on detecting and, if possible, correcting tares, in order to minimise the related loss of information. “Good quality research depends on good quality data and good quality data depends on good quality control methods” (SeaDataNet, Data Quality Control Procedures, 2010). In particular, the following key points are checked: timing (agreement between data and recording date), outlier detection, gap filling, de-spiking, and drift control.

Bearing in mind that a TG is not able to distinguish between sea level variations and the relative movement of the TG (subsidence or lifting of the ground), each station is connected to the levelling network. Periodically, the differences in height between the benchmark closest to the TG and those of the levelling network are measured with a high-precision geodetic levelling. Since October 2015, the station called NAMM, replacing NAPT, has become the reference station. However, throughout the paper we will always refer to the NAPT station, meaning that until September 2015 we have used the data of the NAPT tide gauge and from October 2015 those of the NAMM station. As NAPT, it is located in the harbour of Napoli and it is the first TG co-located with a permanent GNSS station. It is well known that a GNSS permanent station can be used to measure the 3D motion of land points in WGS84 coordinate system. This is a useful approach to distinguish between relative and absolute sea level change: if a trend of land subsidence is measured by GNSS stations, this can be subtracted from the relative sea level variation turning out an estimate of “absolute” sea level change. In fact, according to Wöppelmann and Marcos (2016), while tide gauges can provide an estimate for the rate of relative sea level change (S) with respect to the nearby land represented by the grounded tide gauge benchmarks, the rate of geocentric vertical land motion (U) of these benchmarks can be estimated using GNSS. Hence, a basic expression for the absolute (geocentric) sea level change (N) is the following $U+S=N$.

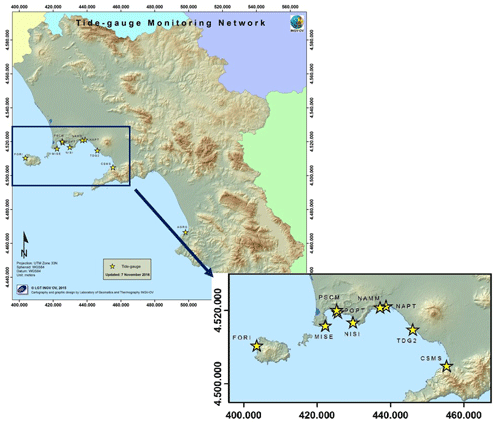
NTGN records water-level oscillations at ten sites (Table 1 and Fig. 1), four stations are located in the Gulf of Napoli (NAMM, NAPT, TRDG, CSMS), 4 in the Gulf of Pozzuoli (POPT, NISI, MISE, PSCM), one at Ischia island (FORI) and one in the Gulf of Salerno (AGRO).

Table 1 NTGN network stations.

Figure 1 Neapolitan Tide Gauge Network (NTGN) managed by Osservatorio Vesuviano, branch of INGV. For clarity, we do not show the GNNS station called RITE, because it is very close to POPT tide gauge. The map was created by the INGV-OV Laboratory of Geomatics and Thermography, © LGT INGV OV, 2015.

3 Data set and Methodology

A database encompassing over 19 years have been organized and validated using, where necessary, statistical gap filling technique. We investigate the oscillations of relative sea level collected at the tide gauges located in Gulf of Pozzuoli (POPT, MISE, NISI, PSCM) and Napoli (NAPT and TDG2) spanning May 1999–December 2018 time interval (Fig. 2). In other words, we study the oscillations of the heights of sea level expressed with respect to an arbitrary and local datum, hence relative to the land upon which the tide gauge is grounded. Furthermore, we consider the GNSS data of the permanent station called RITE to compare the ground displacement measured by it with that detected by the tide gauge.

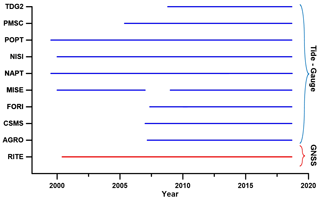
Figure 2 Consistency of the available data set. Red and blue lines indicate GNSS and tide gauges stations respectively. For clarity, the time interval covered by the two reference stations, NAPT and NAMM, is indicated only by name NAPT.

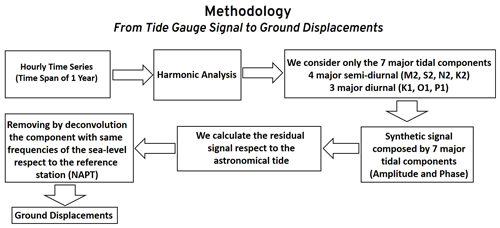
To achieve this purpose, we use the classical harmonic analysis, which models the tidal signal as sum of sinusoids at specific frequencies connected to astronomical parameters (Fig. 3). We perform the harmonic analysis on yearly time series, with temporal sampling of 1 h, using T-Tide code (Pawlowicz et al., 2002). If the focus in the least-squares adjustment is on tidal frequencies, there is no strong argument to introducing shorter sampling intervals than 1 h to tidal and related observations. T-Tide is a package of routines devoted to classical harmonic analysis with nodal corrections, inference, and a variety of user specified options. In this study, we consider only the seven major tidal constituents, four main semidiurnal (M2, S2, N2, K2) and three diurnal (K1, O1, P1). The Rayleigh criterion for resolution limit, of length N time series, sampled at Δt, α(NΔt)⁻¹ (with default α=1) demands a time series length of 182.6 d for the separation of P1 and K1 as well as S2 and K2 frequencies, therefore, the duration of the records of this data set is suitable to resolve the seven main tidal components.

Figure 3 Flowchart of the methodology used in this paper to retrieve ground displacements from the tide gauge signal.

4 Harmonic Tidal and Non-tidal Analysis

Tides and interaction between atmosphere and ocean (e.g., atmospheric pressure fluctuation, wind, oceanic currents, basins shape and bathymetry) can cause time variations of sea level, that generally are analysed in linear (e.g. Munk and Cartwright, 1966) and non-linear (e.g. Capuano et al., 2011) frameworks. Continental blocks motion and melting of icecaps can cause, at lower frequency, apparent changes of the sea level. In active volcanic areas near to the coastline, local apparent changes of sea level can be due to uplift or subsidence associate with volcano dynamics, being therefore an important indicator for the surveillance system. Gravitational forces in the Earth-Moon-Sun system cause the rhythmic rising and lowering of ocean waters resulting in Tide Waves (Melchior, 1978). Because of its much closer position to the Earth, the Moon exerts more than twice a larger force than the tides as the Sun. Hence, the tide closely follows the moon during its rotation around the earth, creating mainly diurnal and semi-diurnal tide and ebb cycles at any particular ocean surface. The amplitude or height of the tide wave is very small in the open ocean (several centimetres), but, due to the principle of conservation of the momentum, it dramatically increases when reaching continental shelves along a coastline. Tidal analysis of data collected by gauges has conventionally two purposes. First, predicting tides at future times as a valuable aid for shipping and harbour operations. Secondly, mapping and interpreting results in terms of the hydrodynamics of the seas and their responses to tidal forcing. Here we target a third non-conventional purpose, namely extracting from the tide gauge records the volcano-tectonic signal (vertical ground displacement). Hence, in our study precise tidal analyses solely aim at a suitable modelling of local tides, alternatively referable as synthetic tide to be reduced in the collected gauge records and hence allow to extract ground displacement of volcanic origin.

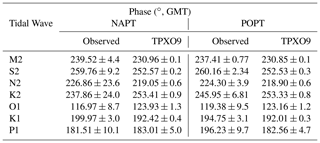
Six month span of sea level data, recorded with a sampling rate of 60 s at NAPT and POPT tide gauges, was subject to spectral analysis to assess the sources of harmonic loading to the sea floor. The two stations in the Bay of Napoli and Pozzuoli are able to record a rich spectrum of tides and harmonic resonances of the sea surface (seiches). Other than tidal signal, the observed spectra reflect the micro-tidal regime and waves, the latter dominated by a cyclonic circulation dependent on both barometric fields and the thermohaline currents. It is renowned that from interaction between wind and sea in enclosed and/or semi-enclosed basin, a peculiar wave, called “seiche”, can rise. Seiches are typically caused when strong winds and rapid changes in atmospheric pressure push water from one end of a water body to the other. When the wind stops, the water rebounds to the other side of the enclosed area. The water then continues to oscillate back and forth for hours or even days. Seiches have a typical spectral signature and, at higher frequencies, this is strongly depending on the bathymetry and coast-to-sea land mask shape. Power spectra (Figs. 4 and 5) show seven tidal components that decay in agreement with decreasing period. The semi-diurnal (2 cycles per day, cpd) band hosts the largest tidal forcing near Pozzuoli and Napoli. Its amplitude is 5 times larger than diurnal and 10 times larger than ter-diurnal (3 cpd) and quarter-diurnal (4 cpd) harmonics. Moreover, at the frequency around 2 cpd sea level oscillations are nearly identical at the POPT and NAPT tide gauges. The amplitudes and phases of the main diurnal and semi-diurnal tidal waves for NAPT and POPT are compared in Tables 2 and 3 with the ones predicted by TPXO9_v2a model (Egbert and Erofeeva, 2002). TPXO9 is a barotropic model (https://www.tpxo.net/global, last access: 9 April 2020) with a resolution of 1∕30^∘, equivalent to about 4 km. Model amplitudes are retrieved from harmonic analyses carried out with ET34-ANA-v7.3 software (Schüller, 2019; Ducarme and Schüller, 2018) on synthetic signals made available at the TPXO web service (https://tpxows.azurewebsites.net/, last access: 10 August 2020).

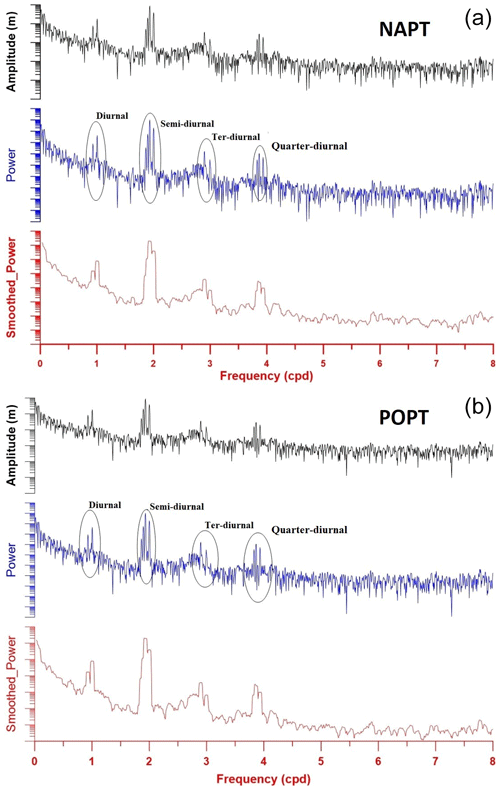
Figure 4 Amplitude, power and smoothed power spectra in the range 0–8 cpd. The black ellipses contain the frequency range of the four tidal species for NAPT (a) and POPT (b) tide gauge station; frequency is expressed in cycle per day (cpd).

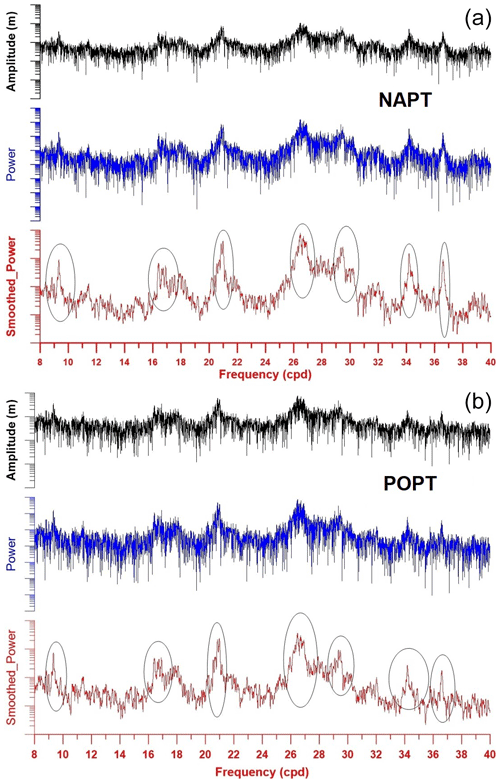
Figure 5 Amplitude, power and smoothed power spectra. The black ellipses contain the frequency range of the seven seiches between 8 and 40 cpd for NAPT (a) and POPT (b) tide gauge station.

Table 2 Observed and predicted by TPX09_v2a model amplitudes of the main seven tidal components for NAPT and POPT.

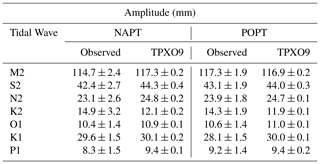
Table 3 Observed and predicted by TPXO9_v2a model phases of the main seven tidal components for NAPT and POPT.

Coherent sea level variations occur at eight frequencies for seiches between 8 cpd (3 h) and 40 cpd (0.6 h). For NAPT and POPT tide gauges, seiche periods at 2.5, 2.1, 1.4, 1.1, 0.9, 0.8, 0.7 h (Fig. 5) show good coherence. But the ratio R (1) between the sea levels recorded at POPT and those measured at NAPT tide gauge in about 30 % of cases departs from unity for more than 10 % (Fig. 6). Seiches are standing waves, so they are characterized by nodes and antinodes. Assuming that inside the gulf there are antinodes, which, being points of maximum amplitude, they make the ratio R deviates from the unity.

$$\begin{array}{}\text{(1)}& R={\displaystyle \frac{\mathrm{\Delta }{H}_{\mathrm{POPT}}}{\mathrm{\Delta }{H}_{\mathrm{NAPT}}}}={\displaystyle \frac{H_{(\mathrm{POPT}{)}_i}-H_{(\mathrm{POPT}{)}_{i-\mathrm{1}}}}{H_{(\mathrm{NAPT}{)}_i}-H_{(\mathrm{NAPT}{)}_{i-\mathrm{1}}}}}\end{array}$$

For periods shorter than 40 min some coherences are quietly evident, but the spectral power varies significantly between POPT and NAPT gauges, allegedly indicating short wavelength resonances near harbours (Fig. 7).

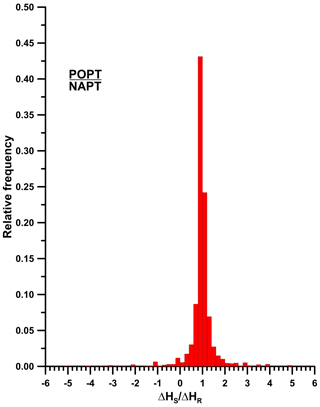
Figure 6 Frequency distribution of the R ratio between sea level daily variations at POPT station and NAPT tide gauge. Positive and negative values indicate that the signals are in phase or in phase opposition respectively.

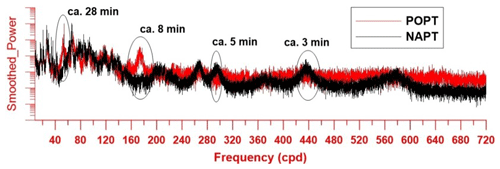
Figure 7 Spectrum of the smoothed power for POPT and NAPT tide gauges in the frequency range 40–720 cpd.

Previous studies of seiches in the Bay of Napoli have identified two characteristic periods of 5.7 h and 55 min respectively attributable to the Tyrrenian Sea (Speich and Mosetti, 1988). Caloi and Marcelli (1949) have observed periods of 58, 48, 22 and 17.8 min. The spectral outcomes lead us to identify the aforementioned seiche periods and numerous other ones.

5 Retrieval of Ground Displacement

A tide gauge record can capture a variety of local and regional phenomena related to decadal climate variability, tides, storm surges, volcano-tectonic driven process, tsunamis, swells, and other coastal processes. When the expected magnitude of the target signal (volcano-tectonic process) is small and the related geodetic signals are elusive, extracting ground displacement from tide gauge records, requires a realistic estimate of uncertainties in geodetic records. Very accurate observations are needed to enhance the signal to noise ratio in two or more tide gauges to discriminate between apparent and effective sea level variation produced by local ground movements.

One can look at tide gauge record as a multi-component signal resulting from the overlapping of different components, whose independence often is physically not easy to fulfill, due to a number of different physical sources working with a periodic and/or transient time behavior.

Each gauge record is made of a deterministic (functional) and stochastic part. Accounting for the fact that correlations between the local ground displacement components are small, then analysis of gauge records can be performed component by component. Indeed, modelling and extraction of the different components, contributing to the collected record, can be a challenging task. It can be done by means of a least-squares fitting independently applied to each site through the following conceptual equation, which represents the relative sea level S_l (t):

$$\begin{array}{}\text{(2)}& S_{\mathrm{l}}\left(t\right)=S_{\mathrm{l}}\left(\mathrm{0}\right)+\mathrm{ST}\left(t\right)+\mathrm{SM}\left(t\right)+\sum _{l=\mathrm{1}}^L{\mathrm{Sd}}_l\mathit{\theta }\left(t_l-t_{\mathrm{0}}\right)+\mathit{\epsilon }\end{array}$$

where, S_l(0) is the relative sea level height at time t₀, ST represent the periodic tidal sea level change due to diurnal and semi-diurnal tides, which is parametrized through the assessment of the parameters (amplitude and phase) for the 7 main tidal components, SM is the contribution due to meteo-marine signal (e.g., atmospheric pressure fluctuation, wind, oceanic currents, storm surge), Sd_l is the ground vertical displacement due to volcano-tectonic process at epoch t_l, θ is the Heaviside function, ε is the stochastic noise term.

As mentioned before, through the harmonic analysis we infer amplitude and phase for the main diurnal and semi-diurnal tide components. Then, we calculate the synthetic tide (Fig. 8) by “relying on” amplitude and phase of the seven components (K1, O1, P1, M2, S2, N2, K2), which are the most relevant around the Neapolitan volcanic area. In principle, the first residual signal, after removing the astronomical tide from the records, should contain information about meteorological component, eustatic, steric changes, ground deformation and noise (Eq. 2). In other words, the signal results from the convolution of many signal components. Therefore, under the assumption of very similar meteo-marine conditions in two gauges few kilometers apart, removing by deconvolution the components with same frequencies of the sea-level respect to a reference tide gauge (NAPT) provides the final residual signal. That final residual (Eq. 2) will contain the uncorrelated noise (ε), plus hopefully small site-dependent effects and, last but not least, it should allow an estimation of the ground level variation.

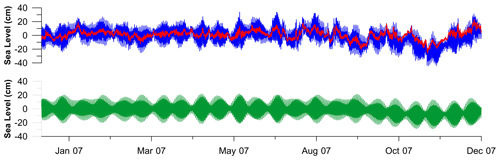
Figure 8 Example of recording collected during the year 2007 at NAPT tide gauge, located in the port of Naples: recorded sea level change (blue line), synthetic signal (green line) retrieved from the assessed tidal constants (amplitude and phase) of the seven main components, and residual signal (red line) with respect to the synthetic one.

We suggest a method to filter out the volcano-tectonic signal from tide gauge records. The idea behind this method is to extract the target signal (bradyseism) by deconvolving it from two records, one collected in the active area (Pozzuoli) and the other in a reference stable station (Napoli).

As aforementioned, we assume that the volcano-tectonic signal is “enwrapped” in POPT residual sea level record [p(t)], which is composed of two components: (1) a residual meteo-marine signal being at some extent similar or even equal to the one collected at NAPT station [n(t)] and (2) the volcano tectonic vertical ground motion [B(t)].

$$\begin{array}{}\text{(3)}& B\left(t\right)=f\left(t\right)-\mathrm{iDFT}{\left({\displaystyle \frac{P\left(\mathit{\omega }\right)}{N\left(\mathit{\omega }\right)}}\right)}_n\end{array}$$

where, P(ω) and N(ω) are the discrete Fourier transforms (DFT) of p(t) and n(t) respectively.

We first compute the cross-spectrum DFT${\left(\frac{P\left(\mathit{\omega }\right)}{N\left(\mathit{\omega }\right)}\right)}_n$ with the aim to extract the common mode between Pozzuoli and Napoli tide gauges having hopefully meto-marine origin that will be subtracted from the signal in the next step.

The last term of the equation represents a deconvolution in the frequency domain, while iDFT is the inverse discrete Fourier transform to reverse back the signal into time domain; the subscript n indicates that the deconvolution ratio has to be normalized before inversely Fourier transforming it.

This fit-remove-deconvolutive approach has been applied to all the stations in the coastal areas of the CFc.

The ground deformations, in Neapolitan volcanic area, are routinely monitored by means of classical technique (like optical leveling and tiltmetry) and satellite technique (like GNSS, SAR and InSAR). For this reason, the vertical ground displacements inferred from the tide gauges are compared with the results of leveling and continuous GNSS data. For an easier comparison with the weekly solutions from RITE GNSS permanent station, the POPT deconvolved signal has been smoothed through a moving average. The results (Fig. 9) show that, in the CFc, the final residual tide gauge signal has a signal-to-noise ratio suitable to detect the so-called mini-uplift episodes occurred in the last years in the caldera. Moreover, the reconstruction of vertical movements retrieved from tide gauge matches the deformation patterns “seen” by the RITE station, the GNSS station closest to POPT tide gauge. We focus on RITE GNSS site (located in Pozzuoli), because of its key location in the point of the maximum uplift in the caldera, the most suitable for studying ground deformation at Campi Flegrei.

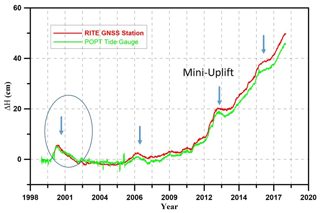
Figure 9 Final tide gauge residual signal (green), namely the ground vertical displacement inferred byfit-remove-deconvolution (see text) at Pozzuoli (POPT). The residual signal is compared to the continuous GNSS data (red line) from RITE, the station closest to the tide gauges. The blue arrows indicate the mini-uplift episode at CFc.

From the visual inspection of the residual POPT signal and RITE GNSS time series some clear episodes of uplift can be identified, (Fig. 9), some (namely, as in the 2000, 2006 and 2014). In particular, the well known uplift episode that during 2000 interrupted CFc's trend of subsidence, which has been studied by Lanari et al. (2004) using InSAR and classical geodetic techniques. They have shown that, starting from March 2000, the continuous GPS stations show the beginning of an uplift episode. With regard to the optical levelling, the measurements from September/October 1999 to May/August 2000 reveal nearly 4 cm of uplift. Moreover, as regards InSAR, a point close to the ACAE GPS station, located in the area with maximum displacements measured, shows “the inversion of the deformation, from subsidence to uplift, after the end of 1999 with a significant uplift from March to August 2000” (Lanari et al., 2004). Before March 2000, the Neapolitan Tide Gauge Network was the only continuous network operating in the area, therefore, it was able to detect, in January, the actual beginning of the uplift (Fig. 9). Furthermore, the TG network has allowed to more accurately describe the entire uplift episode in terms of amplitude of the vertical displacement. In fact, the vertical displacement observed at POPT tide gauge is 6 cm, which is larger than the under estimated value (4 cm) provided by the optical levelling.

6 Retrieval of the Relative Mean Sea Level

As the effects of climate change become more evident, the problem of the sea level rise went worldwide under the spotlights. Sea level change is of great interest for two fundamental reasons. First, changes in the rate of sea level rise are tightly related to changes in the Earth's climate. Second, sea level change has important socioeconomic consequences for populations living in the coastal areas. As clearly the recent news testify reporting on the flooding inundated Venice in November 2019. Thanks to the advent of satellite altimetry, nowadays we have unprecedentedly more information on sea level change than ever before. From satellite altimetry, we know for instance that the geocentric rate of global mean sea level rise over the last decade, corrected for glacial isostatic adjustment (GIA), is nearly 3 mm/yr. This rate is significantly larger than the historical rate of sea level change measured by tide gauges during the same period (in the range of 1–2 mm/yr) (Meyssignac and Cazenave, 2012). Hence, there is a need to distinguish between absolute and relative sea level change. Tide gauges provide valuable observations of relative sea level change (relative to the Earth's crust), but determining absolute sea level change, which is a clue for climate studies, from tide gauge measurements is not straightforward. In fact, observations of absolute sea level change from tide gauge are hampered by two main limitations: (a) tide gauge have poor spatial distribution, being located only on the coasts and ocean islands and therefore do not adequately represent the global oceans; (b) they are tied to the land, which can move vertically, as in the tectonically active areas, thus creating an apparent sea level change that is unrelated to climate variations. Depending on local uplift or subsidence, the change in sea level relative to land observed using tide gauges can vary considerably from place to place and deviates from the rate of global mean sea level (Church et al., 2013). Furthermore, vertical land motion, as in the peculiar volcano-tectonic context of a resurgent caldera, can mask sea level signals associated with climate change and their associated spatial variations.

The mean sea level relative to the global oceans is called the global mean sea level (GMSL). Instead, as already mentioned, the one relative to a particular place is called mean sea level (MSL). The MSL variations usually differ from GMSL ones, because there are phenomena that are present only on a regional and local scale. In addition to climate change, there are long and short term causes that affect the mean sea level, as great fluctuation due to the alternation of glacial and interglacial periods in the last centuries in the Holocene and variations, such as tides, waves and tsunamis.

Several tentative studies have been done to correct tide gauge data for the effects of vertical land motion either through modelling local tectonics or glacial isostatic adjustment (GIA) or by means of direct GPS measurements of the vertical land motion by using geodetically monitored tide gauges (Wöppelmann and Marcos, 2016). To address such kind of problems the availability of co-located tide gauge and GNSS permanent stations is of fundamental importance.

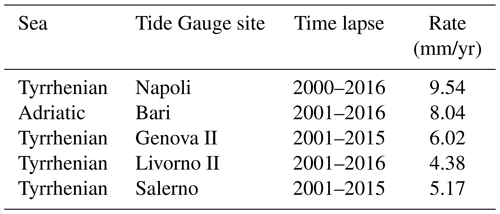
In this study, we evaluate the relative mean sea level (RMSL) in the Gulf of Naples and we compare the trend found in NAPT with that evaluated at four tide gauges. Three located in the Tyrrhenian Sea (Salerno, Livorno II, Genova II) and one station in the Adriatic Sea (Bari). In particular, along the coasts of the Adriatic there are many tide gauges, but we chose the BARI station, located in southern part of the Adriatic sea, because it is outside the northern area affected by a phenomenon of natural and anthropogenic subsidence (Zerbini et al., 2007; Vitaliano et al., 2020).

The stations are managed by ISPRA (Istituto Superiore per la Protezione e la Ricerca Ambientale). Data have been retrieved online from the Permanent Service for Mean Sea Level at http://www.psmsl.org/ (last access: 19 November 2019) (Holgate et al., 2013; PSMSL, 2020).

The four tide gauge stations, in the period considered (2000–2016), have their time series at least 97 % complete. In order not to have artificial signals in the records, the gaps and errors of the data (false zeros and peaks) have been identified and eliminated.

To evaluate the RMSL recorded at NAPT tide gauge, we use the monthly RMSL, and then we subtract the average value. The sea-level time series, with trends and rates as obtained from a linear fit regression of the available data, are reported in the Figs. 10, 11 and Table 4. Due to the short duration of the time series, values are not representative of the long-term trends due to sea level variability. The trend values oscillate between +4.38 and +9.54 mm/yr and the highest value is found in the Naples tide gauge, but in any case of the same order of magnitude as others stations. All time series are affected by large positive sea level anomalies in 2010 and 2011. This is in agreement with Bonaduce et al. (2016) and Landerer and Volkov (2013). In particular, Bonaduce et al. (2016) have highlighted that, in the Mediterranean Sea from 1993 to 2012, there were in all stations analysed large positive sea-level anomalies in 2010 and 2011. Landerer and Volkov (2013) during the same period in the Mediterranean Sea by means of an EEMD (ensemble empirical mode decomposition) approach showed that these events were related to the processes that have dominant periodicities of ∼10 years, and positive residual sea-level trend were generally observed.

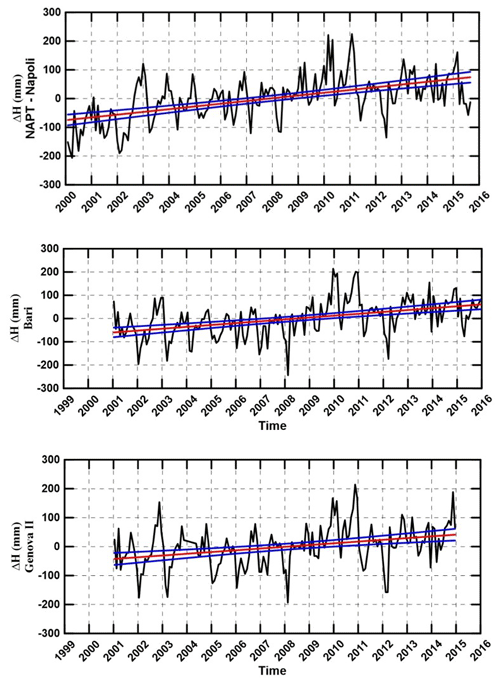
Figure 10 Monthly water level oscillations recorded at ISPRA tide gauges set in Napoli, Bari and Genova (black line); linear fit curve of the sea level (red line) and the two 95 % confidence intervals (blue lines).

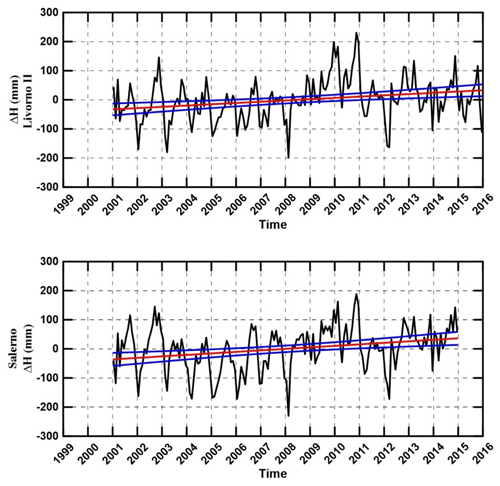
Figure 11 Black line indicates the monthly water level oscillations recorded at ISPRA tide gauges set in Livorno and Salerno. Red line indicates the linear fit curve of the sea level and blues lines the two 95 % confidence intervals.

Table 4 Rates of rise of the MSL evaluated in Adriatic and Tyrrhenian Sea.

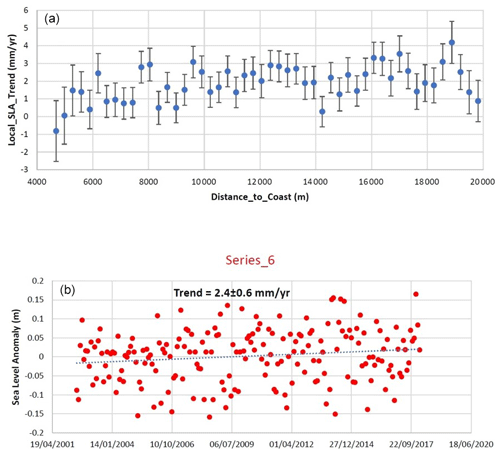
Notwithstanding the limitations hampering the quality of the coastal products of radar altimetry, we have attempted a comparison of tide gauge records with Jason radar altimetry.

The coastal sea level products we use are open access data, derived from the regional coastal along-track product (The Climate Change Coastal Sea Level Team, 2020). We have collected and analysed the Line 237_slot 3, which is the closest to the tide gauges used in our study (Fig. 12). The time series is a 16-year-long (June 2002 to May 2018), high-resolution (20 Hz), along-track sea level dataset in coastal zone of Mediterranean Sea from the Jason-1, Jason-2 and Jason-3 missions. Such products are specifically aimed to derive satellite sea surface ranges as close as possible to the coast. Ad hoc optimization of the geophysical corrections is applied to the satellite range measurements. At each point of measurements along the tracks, the 10 d data are further averaged on a monthly basis, annual and semi-annual signals are removed and a data editing is applied (based on a 2σ elimination of Jason cycles). Finally, the 20 Hz so called sea level anomaly time series is retrieved up to 20 km offshore; details on the processing can be found in The Climate Change Coastal Sea Level Team (2020).

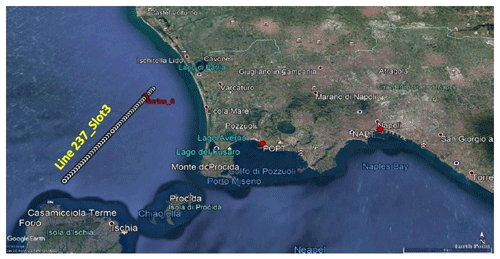
Figure 12 Location of the Line 237_Slot 3 of Jason radar altimetry. Map from Google Earth © Google Earth 2000.

The outcomes (Fig. 13) are quite coherent with the geocentric rate of global mean sea level rise over the last decade, after correction for GIA, that is to say 3 mm/yr (Cazenave et al., 2014). It is even worth to note the typical inverse correlation of the error in radar altimetry ranges with respect to the distance to the coast, due to the above quoted limitations.

Figure 13 (a) shows the monthly local sea level anomaly trend with respect to distance to the coast. (b) shows the monthly time series of one point (Series_6) selected as an example, with indication of least square trend.

7 Conclusions

Mean sea level have been measured throughout the 20th century by means of tide gauges located along shorelines in several countries. Due to a high impact on coastal population, sea level is a very critical variable to study the environment and its changes. Beyond the evaluation of mean sea level trends, tide gauges are a relevant tool for a tidal computation, harbour and navigation operations, sea level hazards warning systems, to estimate extreme weather and climate conditions, as well as, when active volcanoes dominate coastal areas, to assess ground deformation related to the volcano activity.

This study reports on a full spectral analysis, ranging from very long period of relative mean sea level change to high resolution tidal analysis, including seiches, tidal bands and non-linear tides. The spectral analysis has shown that the Gulfs of Napoli and Pozzuoli have a different behaviour and that lead us to identify the seiches periods mentioned in Caloi and Marcelli (1949) and numerous other ones.

As regards the ground displacements, tide gauge signal allows a different sampling of the ΔH with respect to other geodetic techniques, such as GNSS, levelling and SAR. We have applied a fit-remove-deconvolutive approach to the records collected at the tide gauges in the coastal areas of the CFc with respect to Napoli gauge. This has enabled us to extract a clear ground vertical deformation trend in POPT station closely matching the geodetic time series from RITE station, the GNSS station closest to POPT tide gauge. This is a critical sector of the CFC resurgent caldera where the largest uplifts and deformations have been and are still being observed. Our outcomes clearly demonstrate that tide gauges have potentiality to continuously monitoring ground deformations with enough accuracy and resolution and could turn very useful in monitoring rapidly evolving deformation scenarios. Moreover, tide gauge measurements can be used easily in near real time. The tide gauge recordings show that the 2000 uplift episode at Campi Flegrei caldera started already in January and not in March 2000, as mentioned in literature (Lanari et al., 2004). Finally, even though the available TG records are still short and thus non representative of the long-term trends, we preliminarily evaluate the mean sea level trend in Napoli compared with other tide gauge located in the Tyrrhenian and Adriatic sea. Despite their shortness, the sea level time series highlight, in 2010 and 2011, the positive anomalies due to ten-year periodicity.