Earth rotation variations observed by VLBI and the Wettzell “G” ring laser during the CONT17 campaign
Matthias Schartner
André Gebauer
Thomas Klügel
Ulrich Schreiber
Torben Schüler
The VLBI (Very Long Baseline Interferometry) technique can provide the full set of parameters needed for the transformation between celestial and terrestrial reference frames with high accuracy. Yet it has some limitations regarding temporal resolution and continuity, and the accuracy of the resulting Earth Orientation Parameters (EOP) varies depending on the network geometry. In this work we explore the benefit of combining VLBI observations with the measurements of the large ring laser gyroscope “G” in Wettzell for deriving highly resolved ERP (Earth Rotation Parameters, i.e. polar motion and universal time variations, δUT1).
We examine the observations collected by two simultaneously operating VLBI networks during the 15 d of the CONT17 campaign. These two networks, of 14 globally distributed telescopes each, were designed for the estimation of Earth rotation variations, for which reason the resulting hourly ERP are appointed as benchmark in this investigation. To evaluate the advantage of a VLBI and ring laser combined solution, we create degraded versions of the original networks, containing only six stations. The ERP derived from those sparse networks and from the VLBI sparse plus ring laser solutions are then compared in terms of differences to the reference values. It should certainly be considered that these are relative numbers, since they are also determined by the number and selection of the stations remaining in the sparse networks.
The root mean square of the difference to the benchmark is reduced by 24 % in case of δUT1 from one network. The polar motion yp component from the same network moves 14 % closer to the reference value due to the inclusion of the ring laser data. The impact on xp and on all ERP from the other network ranges between 2 % and 9 %.
The research again confirms the feasibility and also the potential gain of a combined evaluation of VLBI and ring laser observations, but the full capacity of such a sensor fusion will emerge once the ring laser gyroscopes reach a level of accuracy similar to VLBI.
- Article
(1517 KB) - Full-text XML
- BibTeX
- EndNote
The Earth's variable rotation can be monitored accurately by space geodetic techniques. Very Long Baseline Interferometry (VLBI) uses Earth-tied station networks to observe signals emitted by extragalactic radio sources and thus establishes a direct link between the terrestrial and the celestial reference frames. If we imply an appropriate network configuration, VLBI is capable of delivering the full set of Earth Orientation Parameters (EOP), i.e. polar motion, nutation (celestial pole offsets) and variation of universal time δUT1 (UT1 − UTC). The quality of the derived EOP depends predominantly on the number and global distribution of the telescopes participating in the observation session.
In this article, we investigate the current potential of combined VLBI and ring laser solutions to compensate for an adverse VLBI network geometry. The large ring laser gyroscope “G” in Wettzell (Germany) is an inertial sensor for Earth rotation variations (Schreiber et al., 2009; Schreiber and Wells, 2013). The device is sensitive to the Earth rotation vector, however, a single ring laser cannot provide all three components. Therefore the ring laser observations have to be processed in combination with other techniques, such as VLBI. The formal connection between the ring laser observation equation and the EOP related to the CIP (Celestial Intermediate Pole) as measured by VLBI is described in Mendes Cerveira (2008) and Mendes Cerveira et al. (2009a). Nilsson et al. (2012) already demonstrated the feasibility of combining VLBI and ring laser data for the estimation of high-resolution polar motion and δUT1. They investigated routine 24 h VLBI sessions and ring laser data for five and a half months in 2010 and evaluated the combination effect by comparing the resulting Earth rotation parameters (ERP) to the sum of the C04 05 EOP series and the conventional model for high-frequency ocean tidal Earth rotation variations (IERS Conventions, 2010), both provided by the International Earth Rotation and Reference Systems Service (IERS). The study yielded a reduction of the average RMS (Root Mean Square) differences, due to the VLBI ring laser combination, of 16 % for the yp component of polar motion, 12 % for δUT1 and showed almost no influence for xp.
Since the publication of that paper the performance of the “G” ring laser has been further improved in several ways. While “G” usually resolves the rotation rate of the Earth to better than 1 part in 108, the shot noise level could be reduced by a factor of 2 and the sensor stability increased by a similar amount. Finally, we have developed an advanced correction model for the scale factor of “G” (Hurst et al., 2017). Ring lasers are referenced to the local inertial frame and have a high temporal resolution of say one minute between data points. This desirable property is a suitable supplement to the very good long term stability of the VLBI technology. Therefore it is of great interest to further investigate the potential of a sensor fusion between a high resolution Sagnac interferometer and the VLBI technique. With the advent of multi-component large ring lasers, such as ROMY (Hand, 2017), a combined evaluation approach may turn out to be of great advantage. For the present study, we employ recent data, obtained in November/December 2017 during the continuous VLBI campaign CONT17. In contrast to Nilsson et al. (2012) we pursue a different strategy of assessing the benefit of a combined VLBI ring laser solution over a VLBI only solution. During CONT17 two independent legacy networks of 14 stations each were scheduled to observe at S/X band in parallel over 15 consecutive days. We estimate hourly ERP from the two original networks and use these as reference solutions. Then we construct artificially diminished versions of the original networks with six stations each and compare the ERP obtained from VLBI only and the VLBI – ring laser combination to the reference solutions.
CONT17 is a campaign of continuous VLBI sessions, which were observed between 28 November and 12 December 2017. Two legacy networks were operating in parallel during the whole observation period for the purpose of demonstrating the highest accuracy of which the legacy S/X system is capable and to test for potential biases between the networks. In order to show the capabilities of the new VGOS (VLBI Global Observing System, e.g. Niell et al., 2018) antennas, a network of six VGOS stations was observing for five days in December as well.
2.1 Observation networks
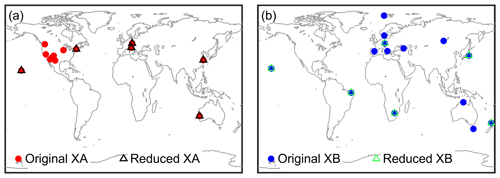
The present study incorporates data of the two S/X networks only. We excluded the VGOS data for different reasons: the short observation time span, the network consisting of merely six stations and the lack of adequate a priori coordinates of the telescopes. It is therefore not feasible to create a benchmark solution for the full VGOS network and a solution from a reduced network, comparable to the approach used for the two legacy networks. These are labeled XA and XB in the following, according to the naming of the respective data files. In the final campaign one Caribbean station could not observe at all due to hurricane damage and some other sites had temporary outages.
Figure 1 shows the original XA and XB networks of 13 and 14 stations (filled circles) together with the sparse networks (triangles) used for the evaluation of the VLBI and ring laser combination. The maps display the quite diverse geometry of the observation set-up. For the XA network, we see a concentration of observing sites in North America and a single station south of the equator, whereas the XB network is dense in Europe and includes five telescopes in the southern hemisphere. The stations of the sparse networks are chosen in a way that preserves the global distribution as far as possible. The definition of the reduced networks is a kind of compromise. On the one hand the networks had to be shrinked enough to see the contribution of the ring laser, whose measurements are still not as precise as those of VLBI. On the other hand the remaining networks should not be too unrealistic, more precisely the intention of the original observation schedules should not be undermined completely, hence we stick at least to the global distribution.
2.2 Preparation of VLBI normal equations
The single session analysis and setting up of the VLBI normal equations are performed with the VLBI module of the Vienna VLBI and Satellite Software VieVS (Böhm et al., 2018). Using vgosDB as input format, we set up single session normal equations for four different networks, for the original XA and XB networks and for the two subnets as depicted in Fig. 1.
We estimate station positions imposing NNR (No Net Rotation) and NNT (No Net Translation) conditions on the coordinates of the stations in ITRF2014 (International Terrestrial Reference Frame 2014, Altamimi et al., 2016). Our target parameters are hourly xp, yp and δUT1, estimated with respect to the sum of the EOP 14C04 series, described by Bizouard et al. (2019), and the conventional models for high frequency Earth rotation variations as recommended in the IERS Conventions (2010). Parameters, which are set up as unknowns in the single session analysis but reduced in the normal equations, are zenith wet delays and troposphere gradients as well as clocks. Celestial pole offsets and source coordinates are fixed to the values of the EOP 14C04 series and of ICRF3 (Charlot, 2018), respectively.
The “G” ring laser in Wettzell, Germany, is currently the most advanced instrument, among a small number of similar devices, which is stable and precise enough to sense the subtle variations of Earth rotation with good fidelity (cf. Schreiber et al., 2011). The rotational motion is sensed against the local inertial frame of reference and the sensor is entirely insensitive to translational motion. The resolution ΔΩ∕Ω0 is between and 10−8 over the length of a day (Schreiber and Wells, 2013) (Ω0 corresponds to the nominal angular velocity of the Earth). In more recent time series a sensitivity of over an integration time of 3 h is reached (Beverini et al., 2016) which translates into a resolution of 0.3 ms in the rate of δUT1 and 0.6 mas in polar motion. A small imbalance in beam power causes a variable bias over longer observation intervals, which is not fully under control at this point in time. Nevertheless, high quality measurements of the ring laser are available for the period of the CONT17 VLBI campaign.
3.1 Measurement principle and performance
The observable of the ring laser is the beat note from the two super-imposed narrow linewidth laser beams in the bi-directional ring cavity, usually referred to as the Sagnac frequency δf, in honor of Georges Sagnac, who exploited this effect for the first time. This beat frequency occurs when the interferometer is rigidly placed on a rotating platform, in our case the local crust. The most notable property of a Sagnac interferometer is the fact that the beat note δf is strictly proportional to the rate of rotation, experienced by the instrument. Of course the local crust is subject to temporal variations of its position with respect to the ITRF which represents the whole Earth. These local tilts are affecting the Sagnac frequency as well and need to be corrected. The size of the instrument defines the ultimate sensor resolution and the mechanical stability determines the sensor drift. The scale factor is given by the perimeter P, the area A circumscribed by the laser beams, the wavelength λ of the laser beams, the unit vector of the surface normal n (pointing outwards) and the experienced rotation vector Ω. The Sagnac frequency is therefore given by
with “⋅” denoting the dot product of vectors.
The square “G” ring in Wettzell is installed horizontally. It encloses an area of 16 m2 and each side is 4 m long. A single ring laser assembled in this way cannot provide all three components of the Earth rotation vector. Three ring lasers with different orientation w.r.t. the terrestrial reference system would be required to access the full Earth rotation vector (Mendes Cerveira et al., 2009b). The terrestrial coordinates of the instantaneous rotation vector are conventionally written as
The functional relation between the usually investigated relative Sagnac frequency δfrel of a horizontally mounted ring laser and the rotation vector is given by Mendes Cerveira (2008)
with ϕ and λ being the nominal geographic latitude and longitude of the ring laser. For the sake of clarity we would like to point out that Eq. (3) is quoted with a wrong sign for the mx component in the two later publications by Mendes Cerveira et al. (2009a, b).
The relative Sagnac frequency is calculated from the nominal Sagnac frequency δf0 and the observed Sagnac frequency δf
3.2 Preparation of ring laser normal equations
In contrast to the ring laser, measurements of the space geodetic techniques do not refer to the instantaneous rotation pole, but to the CIP (Celestial Intermediate Pole). For combining VLBI and ring laser data it is necessary to formulate the observation equations for the same parameters. The conventional EOP (δX, δY, xp, yp, δUT1) can be related to the components of the Earth rotation vector by Eqs. (5)–(7), following Mendes Cerveira et al. (2009a)
where ERA denotes the Earth Rotation Angle. UT1 and ERA are directly related to each other, however the terms proportional to the time derivatives of the celestial pole offsets containing ERA are not considered in the partial derivatives of dδUT1∕dt, but are calculated using the EOP 14C04 δUT1 values as input.
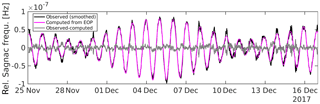
The observation equation of the ring laser as employed for writing the normal equations is built from Eqs. (3) and (5)–(7). The raw Sagnac frequency is corrected for tilt measured by local tiltmeters and then converted to the relative Sagnac frequency δfrel. The theoretical relative Sagnac frequency required to calculate the reduced observation vector for the least squares adjustment is computed from the conventional precession-nutation model IAU (International Astronomical Union) 2000/2006, the EOP 14C04 series and the models for high-frequency Earth rotation variations as recommended in the IERS Conventions (2010). In a combined VLBI and ring laser solution it is necessary to account for unknown offsets and drifts in the ring laser measurements (instrumental effects), as mentioned also by Nilsson et al. (2012). Therefore both series, the observed and the computed relative Sagnac frequency are detrended before the final observed minus computed value is calculated. The reciprocal variance of the observed minus computed values is used to weight the ring laser in the adjustment. Figure 2 shows the detrended observed and theoretical time series and the difference which enters the reduced observation vector. The ring laser raw data have a one minute sampling interval, the values in the image are smoothed for better visibility.
Parameters which are set up in the ring laser normal equations are piecewise linear offsets for xp and yp and offsets for δUT1 and polar motion rates with hourly resolution. The partial derivatives for these parameters can be obtained from the observation equation. Please note that the partials provided in Mendes Cerveira et al. (2009b) are to some extent wrong because the sign mistake, mentioned in the previous subsection, is forwarded to the derived partial derivatives.
In the following section, we will use VLBI to identify VLBI only solutions and VLBI + RL as an abbreviation for the VLBI and ring laser combination solutions. All compared results, VLBI and VLBI + RL, are obtained through the stacking of normal equations over the whole CONT17 period. In VLBI this is called a global solution in contrast to a single session solution. Such global solutions are computed for the fully populated XA and XB networks, for the sparse XA and XB networks and for the combination of the sparse networks with the ring laser. The full VLBI solutions are used as a benchmark to assess the benefit of the combination with ring laser measurements. The combined solutions of the original CONT17 networks with the ring laser are not discussed here, because these networks were designed for the purpose of deriving EOP and the contribution of the ring laser, whose measurements are not yet at the same level of accuracy as those of VLBI, is hardly visible.
4.1 Results from original CONT17 VLBI networks
In the VLBI global solutions, we estimate coordinates using NNR/NNT conditions on the ITRF2014 coordinates of the stations and polar motion and δUT1 as hourly piecewise linear offsets at integer hours. The ERP are estimated with loose constraints in order to avoid outliers during hourly segments with less observations, which is especially important for the solutions from the reduced networks. All other parameters are either fixed to a priori values or reduced according to their introduction to the normal equations (see Sect. 2.2).
The ERP from the full XA and XB networks are compared in terms of estimated offsets to a priori values (EOP 14C04 + high-frequency models) and against one another. These results are shown to give a general impression of the size of the estimates and the level of internal agreement of the VLBI observations. Figure 3a illustrates the mean of the ERP estimates and of the difference XB minus XA. We see considerable biases with respect to the a priori ERP and also between the two networks. The biases can probably be explained by the choice of the a priori ERP and the reference frame. The EOP 14C04 and the ITRF2014 are both multi-technique combination products and it is known that there are biases present among the techniques. For example Bizouard et al. (2019) report about “network effects” which are corrected for within the EOP 14C04 combination procedure.
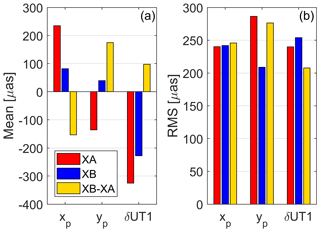
Figure 3Mean (a) and RMS (b) of detrended ERP estimates and differences from the original CONT17 networks.
Figure 3b shows the RMS of the detrended estimates and of the estimates of XB w.r.t. XA. The RMS of the network differences, varying around 250 µas, are in good agreement with the scatter of the estimates, which can be interpreted as a proof of internal consistency.
4.2 Results from VLBI sparse networks and ring laser combination
The global solutions from the reduced VLBI networks are performed analogously to the solutions from the original networks. Within the VLBI + RL combination process, additional condition equations are added to constrain the ERP rates (which are set up for the ring laser) to the estimated offsets.
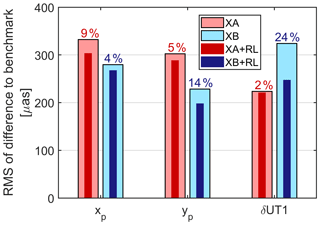
Figure 4RMS of ERP differences between reduced network and benchmark solutions, including percentage of RMS reduction due to ring laser combination.
In Fig. 4 we display the RMS of the differences of the VLBI (sparse) and the VLBI + RL solution to the VLBI benchmark solution for each parameter. Additionally, the reduction of the RMS due to the combination with the ring laser data is specified in percent. The maximum effect of the VLBI + RL combination is found for the δUT1 component from the XB network, where the RMS of the difference to the reference is reduced by 24 %. In the case of the XA network, δUT1 is hardly affected at all. Concerning polar motion, we do not see any tendency towards one component. For XA mainly xp is improved, by only 9 % though, whereas XB experiences higher RMS reduction, of 14 %, in the yp component.
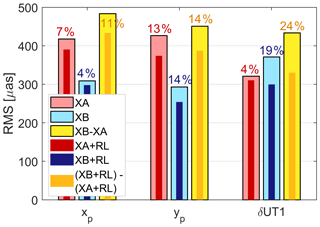
Figure 5RMS of ERP estimates w.r.t. a priori values and differences from VLBI sparse networks and VLBI + RL, including percentage of RMS reduction due to ring laser combination.
We intentionally do not consult the formal errors of the different solutions to evaluate the impact of the ring laser data. Significantly lower formal errors for the combined solutions are to be expected just from the considerably increased number of observations, hence these values are not very conclusive. For reasons of comparability with the work by Nilsson et al. (2012) we also present the RMS of the ERP estimates from the VLBI sparse and VLBI + RL solutions in Fig. 5. In terms of offsets to the a priori values we see a similar impact of the combination regarding xp and δUT1 as in Fig. 4, but slightly different results for the yp component of XA. Considering the average over the two networks we observe that combining VLBI and ring laser yields a reduction of the estimates' RMS of around 5 % for xp, 13 % for yp and 12 % for δUT1. If we take into account that the number and type of the examined VLBI sessions are completely different, these numbers agree more or less with the results of Nilsson et al. (2012). Figure 5 shows additionally that the combination with ring laser data improves the internal agreement between the two simultaneously observed networks. Admittedly, this effect can be anticipated, since both are combined with the same data set.
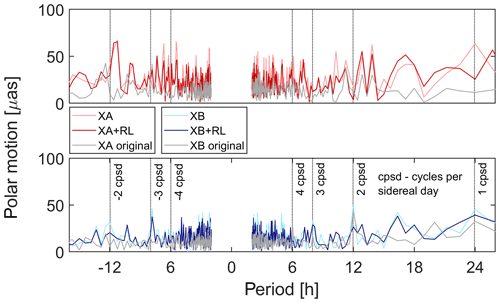
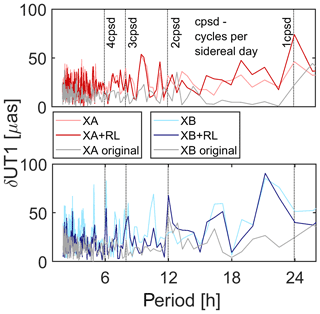
In order to get an impression of the combination implications from another perspective, we switch from time to frequency domain. Figures 6 and 7 contain the amplitude spectra of polar motion and δUT1 variations from the VLBI original and sparse networks and the VLBI + RL combined solutions, derived by FFT (Fast Fourier Transform). Note that the retrograde diurnal part of the polar motion spectra is not displayed in the figure because it is conventionally attributed to nutation. Since a priori nutation is not modelled perfectly and celestial pole offsets cannot be estimated together with hourly polar motion, a diurnal retrograde signal is nevertheless present in polar motion, but it does not add valuable information to the present study.
When comparing the spectra of the pure VLBI solutions we see a generally higher noise level and a number of spurious peaks for the VLBI sparse networks. These peaks are generated by the wilful shrinkage of the observation networks, which certainly introduces systematic errors into the resulting parameters. The schedules were created for the 14 original stations and are of course not at all optimized for the six stations that are extracted for the sparse solutions. Except for the case of δUT1 from the XA network, the combination with ring laser data tends to reduce the noise level and helps to downsize several artificial peaks. Most prominent in terms of polar motion are the peaks at 10.3 and 24 h for the XA network and at −12.0 and 4.9 h for the XB network, where the amplitude differences to the benchmark solutions are decreased by 40 % to 70 %. In terms of δUT1 the improvements achieved with VLBI + RL in frequency domain mirror the results in time domain. In case of the XA network almost no influence of the combination is visible. By way of contrast, the spectrum of the VLBI + RL solution of the XB network is definitely closer to the original XB spectrum than the amplitudes of the δUT1 series from the sparse XB network. For example the amplitude differences at 4.9 and 10.3 h are reduced by more than 80 % by means of combination.
We compare hourly polar motion and δUT1, obtained from two reduced CONT17 VLBI networks and from the combination of these with measurements of the “G” ring laser, to a benchmark solution computed from the original CONT17 XA and XB networks. Looking at the RMS of the ERP differences to the reference solutions, we see the highest impact of the VLBI + RL combination in δUT1 from the XB network, where the RMS is reduced by 24 %. The yp component of XB is improved by 14 %, while the effect for xp and for all ERP of the XA network ranges below 10 %. The comparison of the respective amplitude spectra extensively confirms these findings. Even though the geometry of the reduced XA networks is supposed to be more unfavourable for ERP determination than that of the reduced XB network, the impact of the ring laser is less pronounced. However, the most notable combination benefit in case of XA arises for xp, which could be expected in view of the lack of southern stations.
We conclude that the potential of the ring laser to effectively complement the VLBI technique is there, albeit not very distinct at present. Naturally, the impact shown here is also a consequence of the design of the reduced VLBI networks. With weaker geometry and less stations the ring laser influence would be more visible, while it would be less pronounced or even vanish with more stations. The advantage of a combined evaluation will become obvious, as soon as the accuracy differences between both techniques are further decreased. The physical limits of ring lasers are not yet fully exploited. There is still room for an improvement in beam intensity regulation or active perimeter control in order to increase the instrument stability. Ongoing advances in mirror technology will provide the potential to further reduce the quantum noise limit and to improve the resolution. Yet, the amendment achievable by combining VLBI with the measurements of only one ring laser is probably limited. The vision of an optimal sensor fusion incorporates a network of high resolution Sagnac interferometers to bridge the gaps between successive VLBI sessions and to extrapolate the Earth rotation variations until the next session is correlated and analyzed. In this way the high temporal resolution and continuous observing mode of the ring laser and the accuracy and long term stability of VLBI can be merged to ideally exploit the strength of each system. Of course, high resolution and continuous time series are also provided by the Global Navigation Satellite Systems, but the ring laser technology has the advantages that the results are available almost in real-time and the computational cost is small compared to processing data of a global GNSS network.
The VLBI observation data of CONT17 in vgosDB format is available at ftp://cddis.gsfc.nasa.gov/pub/vlbi/ivsdata/vgosdb/2017/ (last access: 24 October 2019). Ring laser data is not publicly accessible, but can be provided upon request.
AG, TK, US and TS are responsible for maintenance and operation of the “G” ring laser and generated the Sagnac frequency data used for this study. MS prepared the combination software and the ring laser normal equations. SB carried out the VLBI analysis and combination and created the plots. The manuscript was written by SB with text parts and contributions from all co-authors.
The authors declare that they have no conflict of interest.
This article is part of the special issue “European Geosciences Union General Assembly 2019, EGU Geodesy Division Sessions G1.1, G2.4, G2.6, G3.1, G4.4, and G5.2”. It is a result of the EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019.
We are grateful to TU Wien for funding this work within the project “Ring laser gyroscopes for Earth rotation”. We would like to thank Aleksander Brzeziński, Tobias Nilsson and one anonymous reviewer for their valuable comments and suggestions.
This paper was edited by Katrin Bentel and reviewed by Aleksander Brzezinski, Tobias Nilsson, and one anonymous referee.
Altamimi, Z., Rebischung, P., Métivier, L., and Collilieux, X.: ITRF2014: A new release of the International Terrestrial Reference Frame modeling non-linear station motions, J. Geophys. Res.-Sol. Ea., 121, 6109–6131, https://doi.org/10.1002/2016JB013098, 2016. a
Beverini, N., Di Virgilio, A., Belfi, J., Ortolan, A., Schreiber, K., Gebauer, A., and Klügel, T.: High-Accuracy Ring Laser Gyroscopes: Earth Rotation Rate and Relativistic Effects, J. Phys. Conf. Ser., 723, 012061-7, https://doi.org/10.1088/1742-6596/723/1/012061, 2016. a
Bizouard, C., Lambert, S., Gattano, C., Becker, O., and Richard, J.-Y.: The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014, J. Geodesy, 93, 621–633, 2019. a, b
Böhm, J., Böhm, S., Boisits, J., Girdiuk, A., Gruber, J., Hellerschmied, A., Krásná, H., Landskron, D., Madzak, M., Mayer, D., McCallum, J., McCallum, L., Schartner, M., and Teke, K.: Vienna VLBI and satellite software (VieVs) for geodesy and astrometry, Publications of the Astronomical Society of the Pacific, 130, 044503, https://doi.org/10.1088/1538-3873/aaa22b, 2018. a
Charlot, P.: The Third Realization of the International Celestial Reference Frame, Presentation given at the IAU General Assembly 2018, Vienna, Austria, available at: https://www.iau.org/static/science/scientific_bodies/divisions/a/2018/Charlot.pdf (last access: May 2019), 2018. a
Hand, E.: Lord of the rings, Science, 356, 236–238, 2017. a
Hurst, R. B., Mayerbacher, M., Gebauer, A., Schreiber, K. U., and Wells, J.-P. R.: High-accuracy absolute rotation rate measurements with a large ring laser gyro: establishing the scale factor, Appl. Optics, 56, 1124–1130, 2017. a
IERS Conventions: IERS Technical Note; 36, edited by: Petit, G. and Luzum, B., Verlag des Bundesamtes für Kartographie und Geodäsie, Frankfurt am Main, 2010. a, b, c
Mendes Cerveira, P. J.: The Wettzell Ring Laser ”G” as a North-South Tilt Probe, Bulletin d'Information des Marees Terrestres, 144, 11 597–11 604, 2008. a, b
Mendes Cerveira, P. J., Böhm, J., Schuh, H., Klügel, T., Velikoseltsev, A., Schreiber, U., and Brzezinski, A.: Earth Rotation Observed by Very Long Baseline Interferometry and Ring Laser, Pure and Applied Geophysics, 166, 1499–1517, 2009a. a, b, c
Mendes Cerveira, P. J., Spicakova, H., Schuh, H., Klügel, T., Schreiber, U., and Velikoseltsev, A.: Earth Rotation Parameters from VLBI and Ringlaser Observables, Adv. Geosci., 13, 155–165, https://doi.org/10.1142/9789812836182_0010, 2009b. a, b, c
Niell, A., Barrett, J., Burns, A., Cappallo, R., Corey, B., Derome, M., Eckert, C., Elosegui, P., McWhirter, R., Poirier, M., Rajagopalan, G., Rogers, A., Ruszczyk, C., SooHoo, J., Titus, M., Whitney, A., Behrend, D., Bolotin, S., Gipson, J., Gordon, D., Himwich, E., and Petrachenko, B.: Demonstration of a Broadband Very Long Baseline Interferometer System: A New Instrument for High-Precision Space Geodesy, Radio Sci., 53, 1269–1291, 2018. a
Nilsson, T., Böhm, J., Schuh, H., Schreiber, U., Gebauer, A., and Klügel, T.: Combining VLBI and ring laser observations for determination of high frequency Earth rotation variation, J. Geodyn., 62, 69–73, 2012. a, b, c, d, e
Schreiber, K. U. and Wells, J.-P. R.: Invited Review Article: Large ring lasers for rotation sensing, Rev. Sci. Instrum., 84, 041101-26, https://doi.org/10.1063/1.4798216, 2013. a, b
Schreiber, K. U., Klügel, T., Velikoseltsev, A., Schlüter, W., Stedman, G. E., and Wells, J.-P. R.: The large ring laser G for continuous earth rotation monitoring, Pure Appl. Geophys., 166, 1485–1498, 2009. a
Schreiber, K. U., Klügel, T., Wells, J.-P. R., Hurst, R. B., and Gebauer, A.: How to Detect the Chandler and the Annual Wobble of the Earth with a Large Ring Laser Gyroscope, Phys. Rev. Lett., 107, 173904, https://doi.org/10.1103/PhysRevLett.107.173904, 2011. a