Modelling of multi-lateral well geometries for geothermal applications

Well inflow modelling in different numerical simulation approaches are compared for a multi-lateral well. Specifically radial wells will be investigated, which can be created using Radial Jet Drilling (RJD). In this technique, powerful hydraulic jets are used to create small diameter laterals (25–50 mm) of limited length (up to 100 m) from a well. The laterals, also called radials, leave the backbone at a 90^∘ angle. In this study we compare three numerical simulators and a semi-analytical tool for calculating inflow of a radial well. The numerical simulators are FE approaches (CSMP and GOLEM) and an FV approach with explicit well model (Eclipse^®). A series of increasingly complex well configurations is simulated, including one with inflow from a fault. Although all simulators generally are reasonably close in terms of the total well flow (deviations < 4 % for the homogeneous cases), the distribution of the flow over the different parts of the well can vary significantly. Also, the FE approaches are more sensitive to grid size when the flow is dominated by radial flow to the well since they do not include a dedicated well model. In the FE approaches, lower dimensional elements (1-D for the well and 2-D for the faults) were superimposed into a 3-D space. In case the flow is dominated by fracture flow, the results from the FV approach in Eclipse deviates from the FE methods.

1 Introduction

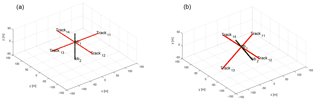
Figure 1 Well configuration for case 1 (a; vertical well with four horizontal laterals) and for case 2 (b; deviated well with four laterals).

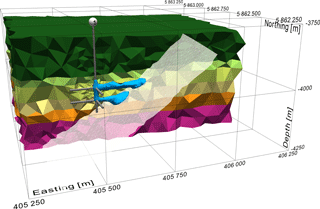
Figure 2 Setup of case 3, which is based on the Groß Schönebeck case and main fault F21n. Also shown are the different rock types, the well including the laterals connecting to fault F21n. For illustration purposes, around the laterals the injected water at the end of an injection period of 5 years is given (in blue).

Geothermal resources can vary widely in their characteristics, depending on the downhole temperature, water composition, depth and the reservoir rock (see e.g. http://geothermalcommunities.eu). For all these applications, production occurs via geothermal wells, which form the link between the subsurface and surface. Planning and operation of the geothermal resource relies on predictions of the performance of the geothermal wells, which is generally done using numerical methods. Different numerical approaches can be used such as finite element (FE), finite difference (FD) or finite volume (FV) or combinations thereof, which rely on different discretisations of the subsurface domain. FE approaches are particularly suitable for mechanical simulations and are generally combined with control volumes for flow simulation (Zienkiewicz and Taylor, 2000). FD is the oldest method and mostly used for flow simulation. In the FV approach, the domain is discretised in volumes rather than distances as in FD, which makes it strongly mass-conservative. This method is particularly suitable for flow modelling on unstructured grids (Eymard et al., 2003). Irrespective of the numerical approach, accurate well inflow modelling is essential. With more complex well geometries becoming possible, accurate simulation of well inflow becomes more difficult (Wolfsteiner et al., 2003). In this study we focus on the well inflow modelling of different simulation approaches for a specific type of well, namely a radial well. This type of well can be created using Radial Jet Drilling (RJD) (e.g. Kamel, 2017). With this technique, powerful hydraulic jets are used to create small diameter laterals (2.5 to 5 cm) of limited length (up to 100 m) from a well. The laterals leave the backbone at a 90^∘ angle and are called “radials”. Generally 10 to 15 of such laterals are jetted in a single well. Currently the technique is best suitable for sedimentary rock with porosity > 5 %, and most implementations are in hydrocarbon reservoirs. For such a radial well configuration, accurate well inflow modelling is more difficult, because of multiple laterals being close together and close to the backbone and with varying diameters. In this study we compare three numerical simulators and a semi-analytical tool for calculating inflow into a radial well. The numerical simulators are FE approaches (CSMP and GOLEM) and an FV approach with explicit well model (Eclipse^®). The semi-analytical tool is based on the Analytical Element Method (AEM). A series of increasingly complex well configurations is simulated, including a case with inflow from a fault. The first two cases which are simulated have homogeneous reservoir properties, because these can be simulated by the semi-analytical tool. In the third case, laterals are used to connect to a fault. The laterals are simplified as straight wells although it is unlikely that they are straight in the subsurface (Reinsch et al., 2018).

Table 1 Settings with fault properties for two fault scenarios.

Table 2 Total flow and relative difference with the results of AEM for all simulators for case 1: vertical well with four laterals.

^* Inflow into the backbone in the presence of laterals.

Table 3 Results for all four simulators for case 2: 35^∘ – deviated well with four laterals (see Fig. 1 the configuration).

Table 4 Increase due to stimulation with four laterals for two cases. Case 1 is a well with a vertical backbone and case 2 is a well with a deviated (35^∘) backbone.

2 Methods

2.1 Description of the simulation codes

2.1.1 Semi-analytical approach (AEM)

The semi-analytic method to estimate the productivity (or injectivity) of a radial well as applied in this paper does not require a spatial discretization and is as such entirely distinctive from the other discussed numerical methods. To allow for a semi-analytic approach, certain simplifications are needed for the geometry and geology of the reservoir. We assume that the radial well is positioned in a cylindrically shaped homogeneous and anisotropic reservoir with laterally a constant pressure boundary condition and a no flow boundary condition at the top and bottom. Due to the complex geometry of a radial well it is likely not possible, even with the above simplifications, to obtain a closed formula for the well's performance (e.g. the Productivity Index that relates drawdown to production rate). The semi-analytic method is based on the AEM (Analytic Element Method) (see Egberts et al., 2013, and Egberts and Peters, 2015, for a more in-depth explanation of the method).

Table 5 Injectivity index (m³ h⁻¹ MPa⁻¹) without radials and with laterals connecting to the fault and the increase from laterals.

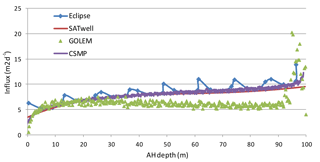
Figure 3 Comparison of the inflow profile for the downward pointed radial (track 13 in Fig. 1) for case 2.

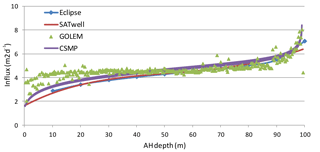
Figure 4 Comparison of the inflow profile for a horizontal radial (track 12 and 14 in Fig. 1) for case 2.

The semi-analytic method provides a solution of the pressure field constructed from analytic solutions for the well segments (backbone and laterals) of the radial well. An important component to arrive at the semi-analytic solution is to model each well segment by a line sink (or line source in case of injection) of the (steady state) pressure equation with a variable influx along the line. The variable influx profile along a well segment is described by a polynomial of an order n, typically less than 10. The coefficients of the polynomials are then exploited to satisfy a prescribed boundary condition at the well such as a constant bottom hole pressure. This is done by distributing so-called control points along the well bore face of the segments and requiring that the pressure solution satisfies the bottom hole pressure at these points.

2.1.2 ECLIPSE

Eclipse^® is an industry-standard simulator used extensively in the petroleum industry and to a lesser extent for geothermal applications (Schlumberger, 2016). The simulator uses a finite volume approach and employs a well model to estimate the pressure drop between the well to the grid block in which it is located based on the approach of Peaceman (1983). This allows for much larger (> 10 m) grid blocks than well radii (∼ 0.1 m) and simulation of multiple wells in a single reservoir model. A well is discretised in a number of well connections (well nodes) with each connection associated to a grid block intersected by the well. We will call a grid block intersected by the well a well block and the intersection a well segment. The well index WI_i of well segment i is defined as (e.g. Wolfsteiner et al., 2003):

$$\begin{array}{}\text{(1)}& {\displaystyle }{q}_i={\displaystyle \frac{{\mathrm{WI}}_i}{\mathit{\mu }}}\left(p_{b,i}-p_{w,i}\right)\end{array}$$

with μ the viscosity. WI_i relates the difference of well pressure p_w,i and gridblock pressure p_b,i to the flow rate q_i for a segment i and depends on the length and diameter of the well segment and the well block size and permeability. Also the orientation of the well with respect to the axis of the grid influences the value of the WI. The WI can be calculated by Eclipse from given well geometry and grid properties or can be calculated in a pre-processing step and be provided to Eclipse. The latter has been done in this paper, where the WI is calculated by Petrel^®, a package for geological modelling. In a well block i, at the point of the backbone where the laterals emerge, the well indices WI_j,i of the different well segments, labeled by index j, need to be amalgamated to a single total well index (WI_t,i). In this case WI_t,i is calculated as:

$$\begin{array}{}\text{(2)}& {\displaystyle }{\mathrm{WI}}_{t,i}={\sum }_{j=\mathrm{1}}^n{\mathrm{WI}}_{j,i}.\end{array}$$

2.1.3 GOLEM

The numerical simulator GOLEM is an open source software for solving parallel tightly coupled non-linear THM processes in fractured reservoir (Cacace and Jacquey, 2017). It is based on the MOOSE framework (Gaston et al., 2009) and its internal architecture relies on state of the art libraries for finite element analysis (libMesh, Kirk et al., 2006) and nonlinear iterative algebraic solvers (PETSc, Balay et al., 2016). GOLEM is based on the finite element method using irregular tetrahedral meshes. The major complication of using irregular meshes is to maintain the internal geometric consistency between well, fracture and matrix elements. This requires each well element to be mapped onto an edge (1-D representation) and each fracture/fault element mapped onto a face (2-D representation) of at least a single 3-D matrix element. In the current study, the well is simulated as a 1-D element superimposed in the 3-D domain, which consists of tetrahedrons. The refinement of the 1-D well-path strongly determines the pressure drop near the well and thus the productivity/injectivity of the well.

2.1.4 CSMP

Complex Systems Modelling Platform (CSMP) is an object-oriented application programme interface (API), for the simulation of complex geological processes and their interactions (formerly CSP, cf. Matthäi et al., 2001). CSMP is based on the finite element method (FEM) and finite element – finite volume (FE-FV) method. CSMP has been utilised to develop coupled thermo-hydro-mechanical-chemical (THMC) model for simulation of subsurface processes (Salimzadeh et al., 2017, 2018). Fractures/faults and wells are modelled using lower dimension elements, i.e. surface elements for fractures/faults and line elements for wells, while the rock layers are modelled using 3-D volume elements. In CSMP, the spatial discretization can be achieved using both structured and unstructured meshes, providing flexibility for different applications. Since the wells are modelled using 1-D elements, like in GOLEM the pressure response is highly mesh dependent. To remove this well-known issue, the size of the tetrahedral connected to the well has been reduced such that the position of the nearest integration point, to the well, where the integrand is being evaluated numerically, resembles the well radius. With this strategy, CSMP results provide a very good fit to the analytical results for the simple geometry wells as discussed later in the results section. A basic well model based on the Peaceman approach (Peaceman, 1983) is available within CSMP, but was not used in this study.

2.2 Description of the cases

2.2.1 Case 1

The first case is a vertical well with a single kickoff with four orthogonal and horizontal laterals in a homogeneous, anisotropic reservoir of 100 m thick (from 2500 to 2600 m depth) (see Fig. 1). The initial pressure is 25 MPa (at 2500 m depth) with a hydrostatic pressure distribution in the vertical. Horizontal permeability is 200 mD, vertical permeability is 20 mD and porosity is 0.2. The lateral boundary condition is a constant pressure boundary on the edge of the model, which is at 1000 m from the well. Top and bottom of the reservoir are no flow boundaries. The reservoir fluid is water with a salinity of 150.000 ppm, which has, at reference pressure, a viscosity of 0.54 cP and density of 1110.2 kg m⁻³. The simulations are isothermal. The well is operated as an injector with a fixed injection pressure of 26 MPa @ 2500 m depth. Thus, the steady state flow rate for a pressure difference of 1 MPa is calculated. Because gravity and water and rock compressibility are not accounted for in AEM, the settings of the numerical simulators has to be adjusted in order to be comparable. Therefore compressibility is set extremely low: rock compressibility is 10⁻⁹ 1∕MPa and water compressibility 10⁻⁶ 1∕MPa and the gravitational acceleration is set to 0.

For GOLEM an element size of 0.32 m for both the backbone and the laterals was selected, because this gave results that most closely matched the semi-analytical solution. For CSMP an element size of 1.5 m for the backbone and 0.2 for the radials was selected for the same reasons. Grid size for the Eclipse model was 10 × 10 × 2.5 m and was not tuned to the results of the semi-analytical solution. The well and laterals in the Eclipse model are defined in the middle of the grid blocks were possible.

2.2.2 Case 2

For case 2, the reservoir is identical to the reservoir in case 1. Only the well configuration is changed to a deviated well (see Fig. 1). The backbone has an inclination of 35^∘ with respect to the vertical. The laterals leave the backbone at a 90^∘ angle. This case is numerically more challenging because the well is not aligned with the main direction of the anisotropic permeability and for Eclipse is not aligned to the grid.

2.2.3 Case 3

For case 3 a low permeability reservoir is selected with a single large fault. The case is based on the Groß Schönebeck case and details of the reservoir properties and the reservoir fluids can be found in Blöcher et al. (2010) and Blöcher et al. (2015). For simplicity reasons only 1 fault (F21n) and 1 well were considered for the simulation. The well itself has 8 radials with 2 kickoff points at −4000 and −4050 m, respectively (Fig. 2). Each kickoff point has 4 radials with a length of at least 100 m each. The two radials in the direction of the fault are increased in length to ensure they intersect the fault. Although extensions of more than 100 m are currently not technically feasible, this scenario has been assumed to test the simulation capabilities. For the fault, two scenarios are defined with different transmissivity to mimic: (Scen. 1) a highly conductive fluid pathway and (Scen. 2) a hydraulically invisible fault zone. The transmissivity T (Table 1) is obtained by the product of the permeability k and the cross-sectional flow area A = w⋅a, where w denotes the fault width (assumed to be 1 m) and a denotes the fault aperture. The permeability of fault is approximated using the Hagen-Poiseuille solution of the Navier Stokes equation for laminar flow between two parallel plates separated by a constant aperture a:

$${\displaystyle }T\cong k_{xy}A={\displaystyle \frac{w{a}^{\mathrm{3}}}{\mathrm{12}}},$$

which expresses the so-called cubic law (Witherspoon et al., 1980).

3 Results

3.1 Case 1 and 2

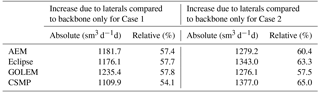
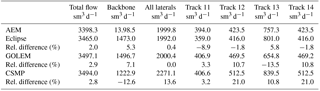
In Table 2, the calculated flow is presented for the vertical well with four horizontal laterals. The relative difference is reported with respect to the semi-analytical tool AEM. The flow rates obtained by AEM, Eclipse and CSMP are 3241.8, 3214.4, and 3161.0 sm³ d⁻¹, respectively. AEM, Eclipse and CSMP are within 2.5 % from each other in terms of the total flow. The results obtained by GOLEM (3374.0 sm³ d⁻¹) shows a 4.1 % larger flow rate in comparison to AEM. Table 3 summarizes the results for case 2. For the deviated well and laterals the difference between the simulators becomes larger (up to 21 %), although the total flow of the well is within 3 % of each other for all simulators. Figures 3 and 4 show the inflow into the downward pointing (track 13) and horizontal lateral (tracks 12 and 14) respectively. The inflow by the numerical simulators is not always smooth as a result of the spatial discretization (e.g. GOLEM and Eclipse for the downward pointing lateral in Fig. 3), which can give rise to inaccuracies. Table 4 shows the increase in flow rate (for a fixed pressure difference) achieved as a result of stimulation of the well with four laterals. This is calculated by comparing the results of a run with and without laterals. For case 1 the increase of flow rate predicted by AEM is 57.4 %. Only the estimated increase by CSMP is somewhat lower at 54.1 %. For case 2, the increase of flow rate predicted by AEM is 60.4 %. The numerical simulators Eclipse and GOLEM are quite close with an increase in flowrate of 63.3 %, 57.5 %, while CSMP deviates a bit more at 65.0 %.

3.2 Case 3

For case 3, only Eclipse and GOLEM are used to simulate the flow, because the semi-analytical tool cannot handle fracture flow and the results of CSMP and GOLEM are very similar if the same gridding is used. The differences between these simulators mostly arise from differences in the elements and refinement of the elements near the well and laterals. Overall the injectivity is lower for Eclipse than for GOLEM (Table 5). The difference between GOLEM and Eclipse is largest for the low permeability fault with laterals: 48 %. In general, connecting to a previously unconnected fault is highly beneficial for the injectivity in the well. It should be noted however, that for commercial rates a considerable number of laterals should be achieved since the diameter of the laterals are small and thus the flow through the laterals is limited.

4 Summary and conclusions

Although all simulators generally are reasonably close in terms of the total well flow (deviations < 4 % for the homogeneous cases), the distribution of the flow over the different parts of the well can vary up to 20 % for some laterals. For the homogeneous cases (1 and 2), the predictions of increase of flow as a result of stimulation by RJD show a range of variation up to 5 % just from differences between numerical solutions even for a simple setup. In realistic implementations with heterogeneous reservoir properties, larger uncertainty from the numerical solution can be expected for all simulators: for Eclipse because of inaccuracies in the calculation of the well index and for the FE approaches because of difficulties in determining the correct mesh size and large number of elements. In case the flow is dominated by fracture flow (case 3), the results deviate more with up to 50 % difference in the predicted flow rate in the case of radials. Even though these uncertainties are considerably smaller than those arising from uncertainty in the properties and uncertainty in the radial path, it is a source of errors that is often ignored.