Large-scale assessment of Prophet for multi-step ahead forecasting of monthly streamflow
Georgia A. Papacharalampous
We assess the performance of the recently introduced Prophet model in multi-step ahead forecasting of monthly streamflow by using a large dataset. Our aim is to compare the results derived through two different approaches. The first approach uses past information about the time series to be forecasted only (standard approach), while the second approach uses exogenous predictor variables alongside with the use of the endogenous ones. The additional information used in the fitting and forecasting processes includes monthly precipitation and/or temperature time series, and their forecasts respectively. Specifically, the exploited exogenous (observed or forecasted) information considered at each time step exclusively concerns the time of interest. The algorithms based on the Prophet model are in total four. Their forecasts are also compared with those obtained using two classical algorithms and two benchmarks. The comparison is performed in terms of four metrics. The findings suggest that the compared approaches are equally useful.
- Article
(2378 KB) - Full-text XML
-
Supplement
(585 KB) - BibTeX
- EndNote
There are two different approaches to statistical time series forecasting regarding the exploited information for obtaining the forecasts. The first approach, known as the standard one, exclusively uses endogenous predictor variables, while the second approach also uses exogenous predictor variables (Hong and Fan, 2016; Hyndman and Athanasopoulos, 2018; see also the Supplement for some basic forecasting terminology used throughout the paper). Moreover, the number of the primary forecasting models is limited (Hong and Fan, 2016), while recent research in geoscience by Tyralis and Papacharalampous (2017), and Papacharalampous et al. (2018a, b, c) suggests that the forecast quality could hardly be improved in a long term run by moving from one forecasting algorithm to another. On the contrary, Hong and Fan (2016) emphasize that the use of appropriate exogenous predictor variables could considerably improve the forecasts. The exogenous predictor variables to be utilized for solving a specific forecasting problem could result through large-scale comparisons (since the results may vary significantly depending on the case study; Papacharalampous et al., 2017b) that precede the application of interest. Such comparisons are known to facilitate benchmarking and model assessment, and require large datasets.
Monthly streamflow or river discharge forecasting is of practical importance. There are several studies approaching this specific problem without utilizing exogenous predictor variables (e.g. Ballini et al., 2001; Koutsoyiannis et al., 2008; Papacharalampous et al., 2017a), while examples of case studies adopting the alternative approach can be found in Callegari et al. (2015) and Yang et al. (2017). The results of such studies are usually presented in terms of point forecasts (hereafter forecasts) rather than in a probabilistic way, as in Tyralis and Koutsoyiannis (2014). An extensive study on the use of climate index data for forecasting monthly streamflow at 88 locations in Brazil is available in Silveira et al. (2017). Another relevant and large-scale study by De Gregorio et al. (2018) uses data originating from 300 alpine basins. Finally, Sun et al. (2014) explore the usefulness of two sets of exogenous predictor variables for one-step ahead forecasting of monthly streamflow in 438 USA catchments using the MOPEX dataset (Schaake et al., 2006). The algorithms implemented in Sun et al. (2014) are the Gaussian process, AutoRegressive Moving Average with eXogenous predictor variables (ARMAX) and MultiLayer Perceptron (MLP).
Herein we expand this latter study by investigating the utility of three different sets of exogenous predictor variables in multi-step ahead forecasting of monthly streamflow. We use a more recent dataset, i.e. the CAMELS dataset (Addor et al., 2017a, b; Newman et al., 2014, 2015), which is also larger than the MOPEX one. We implement Prophet, a forecasting model introduced by Taylor and Letham (2018) that provides the possibility of incorporating exogenous predictor variables. This model was first used in its standard mode for forecasting geophysical time series, specifically monthly precipitation and temperature time series, in Papacharalampous et al. (2018c). We compare the results provided by four variations of the Prophet model with those of two classical algorithms and two benchmarks.
Here we present the data and methods, while the reader is also referred to the Supplement, the code availability section and the data availability section for additional related information. We use the CAMELS dataset, which includes daily streamflow, precipitation and temperature data for 671 USA catchments. We exclude from the analysis all catchments including datasets containing missing values and, finally, we form the mean monthly time series of streamflow, precipitation and temperature for the remaining 513 catchments. In Fig. 1 we present the retained catchments. The retained monthly data span from January 1980 to December 2013 (408 monthly values). A brief exploration of the formed time series of monthly streamflow is displayed in Fig. S1 (see Supplement). The seasonality pattern is obvious in the sample autocorrelation function (ACF) of the original time series and reduced in the sample ACF of the deseasonalized time series, while the estimates of the Hurst parameter (H) of the Hurst-Kolmogorov process (for its definition see Supplement; see also Tyralis et al., 2018), when the latter is fitted to the deseasonalized time series as described in Tyralis and Koutsoyiannis (2011), have a median value of 0.75 and, therefore, indicate significant long-range dependence. We note that the parameter H is commonly used in the literature for measuring this dependence under the established assumption that the latter is present in the various geophysical processes. Moreover, in Fig. S2 (see Supplement) we present the Pearson's correlations between the monthly streamflow and precipitation variables, and the monthly streamflow and temperature variables. The former range between −0.37 and 0.92 with a median of 0.58, and the latter range between −0.76 and 0.75 with a median of −0.21. These correlation values are non-negligible.
We fit a variety of algorithms to the monthly values of the years 1980 to 2012 (fitting period) and forecast the monthly values of year 2013 (forecast period). We implement five forecasting algorithms that exclusively use endogenous predictor variables, namely the Naïve 1, Naïve 2, ARFIMA, SES and Prophet 1 algorithms. The two former algorithms are based on the monthly values of the last year and the average monthly values respectively, while they serve as benchmarks within our methodological framework (see also Hyndman and Athanasopoulos, 2018, chap. 2.3). ARFIMA is an automatic AutoRegressive Fractionally Integrated Moving Average algorithm available in the forecast R package (Hyndman and Khandakar, 2008; Hyndman et al., 2018). SES (Simple Exponential Smoothing) and Prophet 1 are also automatic algorithms. The former is implemented through the forecast R package and the latter through the prophet R package (Taylor and Letham, 2017).
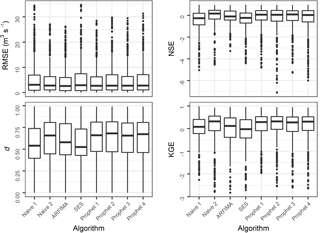
Figure 2Metric values for the 513 catchments presented in an aggregated form. The far outliers (if any) have been removed.
Since the ARFIMA and SES algorithms are suitable for forecasting normal non-seasonal data, we apply these algorithms to the normalized (through Box-Cox transformation) deseasonalized time series. The deseasonalization precedes the normalization and is performed by applying a multiplicative model of time series decomposition (see Hyndman and Athanasopoulos, 2018, chap. 6.3) to the original monthly values of the fitting period and by subsequently dividing the latter values by the estimated seasonal component, while seasonality is recovered in the produced forecasts. The same procedure is adopted for the Prophet 1 algorithm, in spite of the fact that the utilized Prophet model offers the possibility of internally handling of the seasonality. This choice is made, since the external seasonality handling is shown to lead to slightly better forecasts in Papacharalampous et al. (2018c), as well as for consistency purposes with respect to the application of ARFIMA and SES. The handling of the non-normality in the Prophet 1 algorithm is made as default. For a brief description of the ARFIMA, SES and Prophet models see Supplement (see also Papacharalampous et al., 2018c, and the references therein).
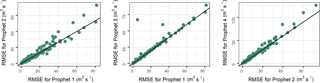
Figure 3Comparison of the RMSE values for the 513 catchments as computed for three pairs of algorithms using the Prophet model. The RMSE values are presented in an aggregated form.
Additionally to the above-described algorithms, we implement the Prophet 2, Prophet 3 and Prophet 4 ones, which utilize exogenous predictor variables alongside with the endogenous ones. Specifically, in Prophet 2 St, i.e. the mean monthly streamflow at time t, is also considered to depend on Pt, i.e. the mean monthly precipitation at time t, as measured for the fitting period and forecasted for the forecast period (seasonality included). We use the forecasts of Pt at the forecast period because the test set should not contain information which was unknown at the time that the forecast was performed. The respective exogenous predictor variables for Prophet 3 and Prophet 4 are Tt, and Pt and Tt respectively, where Tt is the mean monthly temperature at time t. Tt is used as measured for the fitting period and forecasted for the forecast period (seasonality included). The precipitation and temperature forecasts are produced by the Prophet 1 algorithm, while seasonality and non-normality are handled as in Prophet 1. The same applies to the streamflow information utilized by Prophet 2, Prophet 3 and Prophet 4. We note that all the algorithms implemented herein are designed to fit to the data very fast. The large-scale forecasting experiment of this study takes about an hour to run in a regular home PC.
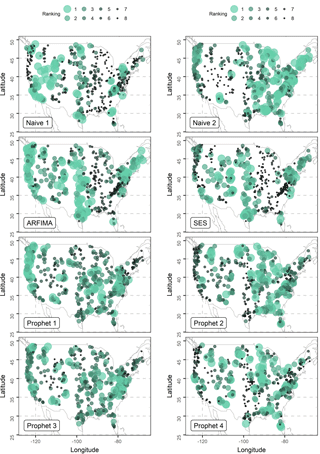
Figure 4Rankings of the algorithms according to the RMSE metric. The algorithms are ranked from best (1st) to worst (8th).
We assess the forecast quality using the RMSE (Root Mean Square Error), NSE (Nash-Sutcliffe Efficiency), d (index of agreement) and KGE (Kling-Gupta Efficiency) metrics. For their definitions see Supplement (see also Papacharalampous et al., 2018a, Supplement, and the references therein). These metrics can take values between 0 (optimal) and +∞, −∞ and 1 (optimal), 0 and 1 (optimal), and −∞ and 1 (optimal) respectively. We present the metric values in an aggregative form, while we also use them to rank the forecasting algorithms.
Section 3 is devoted to the exploration of the results and the discussion of the main findings. In Fig. 2 we present the side-by-side boxplots of the metric values (far outliers excluded). We observe that the Prophet 1, Prophet 2, Prophet 3 and Prophet 4 algorithms produce comparable results with each other. However, the Prophet 1 algorithm produces slightly better forecasts in terms of RMSE and NSE. The same applies to Prophet 2 for the d and KGE metrics. Moreover, in Fig. 3 we present a comparison of the computed RMSE values (far outliers included) for the {Prophet 1, Prophet 2}, {Prophet 1, Prophet 3} and {Prophet 2, Prophet 4} pairs of algorithms. The closeness in the performance of these four algorithms is also perceivable by the examination of this figure, while some few larger differences favouring the Prophet 1 algorithm are observed as far outliers. We further notice that the use of precipitation information seems to affect more than temperature information the forecasting performance. The use of both types of information, on the other hand, mostly results to the largest outlier RMSE values. Importantly, the fact that the use of these specific exogenous predictor variables did not (significantly) improve the performance of the algorithms in any of the 513 cases examined herein should be viewed as a lesson learned from this study.
In fact, the selection of appropriate exogenous variables is far identified in the forecasting literature as a target and challenging at the same time problem to be solved (see, for example, Hong and Fan, 2016), while several approaches not relying on exogenous information are mostly of the same usefulness, especially in geosciences, for which small differences in the forecasting performance of the algorithms do not have any practical effect on decision-making (see also Papacharalampous et al., 2018a). This conclusion can be drawn based on the large-scale results of Tyralis and Papacharalampous (2017) and Papacharalampous et al. (2017a, 2018a, b, c). Here as well, the differences in the results obtained using the various forecasting algorithms are mostly small, while Naïve 1 and SES are in average the worst performing. On the contrary, Naïve 2 performs well, almost as well as the best performing algorithms, i.e. Prophet 1 and ARFIMA. This good performance of Naïve 2 is particularly interesting, while it provides a good reason for always implementing naïve algorithms alongside with more advanced techniques, as also emphasized by forecasting experts (Hyndman and Athanasopoulos, 2018).
Finally, in Fig. 4 we comparatively present the rankings of the implemented algorithms within the conducted experiment according to the RMSE metric. We observe that each of the algorithms may perform better or worse compared to the rest depending on the examined case study. This figure is particularly interesting, especially when viewed in comparison to several studies presenting new techniques and reporting on their superior performance to others based on case studies, while it also confirms in an illustrative way the related to the “no free lunch theorem” findings of Papacharalampous et al. (2017b, 2018a, c). According to the no free lunch theorem, there is not a model which will always perform better than other models (Wolpert, 1996). We integrate Fig. 4 by also providing Figs. S3 and S4 (see Supplement). These figures present the number of times that each algorithm is ranked from best (1st) to worst (8th) and the average rankings of the algorithms respectively. The best average ranking is computed for Prophet 1 and is equal to 3.87, followed by Prophet 3 and Naïve 2 with average rankings equal to 3.94 and 3.95 respectively. SES is the worst performing according to this criterion with an average ranking equal to 5.58. The remaining methods are in between with average rankings 4.18 (ARFIMA), 4.34 (Prophet 2) and 4.89 (Prophet 4).
We implement the recently introduced Prophet model to compare the results obtained via two different approaches to multi-step ahead forecasting of monthly streamflow. The first approach uses endogenous predictor variables only, while the second one also uses observed and forecasted information (as available at the time of the forecast) about monthly precipitation and/or temperature. In the latter approach, the value(s) of the exogenous predictor variables considered at each time step exclusively concern the time of interest. The implementation is made for 513 USA catchments using the CAMELS dataset. The results indicate that the compared approaches produce equivalent results. Future work could focus on the selection of appropriate exogenous predictor variables as proposed by Hong and Fan (2016).
The R code is available upon request to the corresponding author. The analyses were performed in R Programming Language (R Core Team, 2018) using the R packages devtools (Wickham et al., 2018), forecast (Hyndman and Khandakar, 2008; Hyndman et al., 2018), fracdiff (Fraley et al., 2012), gdata (Warnes et al., 2017), ggplot2 (Wickham, 2016; Wickham and Chang, 2016), HKprocess (Tyralis, 2016), knitr (Xie, 2014, 2015, 2018), lubridate (Grolemund and Wickham, 2011; Spinu et al., 2018), maps (Brownrigg et al., 2018), prophet (Taylor and Letham, 2017), readr (Wickham et al., 2017), rmarkdown (Allaire et al., 2018), stringi (Gagolewski, 2018), zoo (Zeileis and Grothendieck, 2005; Zeileis et al., 2018).
The data used in the present study is available in the CAMELS dataset (Addor et al., 2017a, b; Newman et al., 2014, 2015). The daily precipitation included in the latter was obtained by Thornton et al. (2014).
The supplementary document includes basic forecasting terminology, background information on methods and models, and additional figures.
The supplement related to this article is available online at: https://doi.org/10.5194/adgeo-45-147-2018-supplement.
The authors declare that they have no conflict of interest.
This article is part of the special issue “European Geosciences Union General Assembly 2018, EGU Division Energy, Resources & Environment (ERE)”. It is a result of the EGU General Assembly 2018, Vienna, Austria, 8–13 April 2018.
We thank the Editor Luke Griffiths and one anonymous reviewer, whose comments
have led to the improvement of this paper.
Edited by: Luke Griffiths
Reviewed by: Luke Griffiths and one
anonymous referee
Addor, N., Newman, A. J., Mizukami, N., and Clark, M. P.: Catchment attributes for large-sample studies, UCAR/NCAR, Boulder, CO, https://doi.org/10.5065/D6G73C3Q, 2017a.
Addor, N., Newman, A. J., Mizukami, N., and Clark, M. P.: The CAMELS data set: catchment attributes and meteorology for large-sample studies, Hydrol. Earth Syst. Sci., 21, 5293–5313, https://doi.org/10.5194/hess-21-5293-2017, 2017b.
Allaire, J. J., Xie, Y., McPherson, J., Luraschi, J., Ushey, K., Atkins, A., Wickham, H., Cheng, J., and Chang, W.: rmarkdown: Dynamic Documents for R, R package version 1.9, available at: https://CRAN.R-project.org/package=rmarkdown (last access: 15 August 2018), 2018.
Ballini, R., Soares, S., and Andrade, M. G.: Multi-step-ahead monthly streamflow forecasting by a neurofuzzy network model, IFSA World Congress and 20th NAFIPS International Conference, 992–997, https://doi.org/10.1109/NAFIPS.2001.944740, 2001.
Brownrigg, R., Minka, T. P., and Deckmyn, A.: maps: Draw Geographical Maps, R package version 3.3.0, available at: https://CRAN.R-project.org/package=maps (last access: 15 August 2018), 2018.
Callegari, M., Mazzoli, P., de Gregorio, L., Notarnicola, C., Pasolli, L., Petitta, M., and Pistocchi, A.: Seasonal streamflow forecasting using support vector regression: a case study in the Italian Alps, Water, 7, 2494–2515, https://doi.org/10.3390/w7052494, 2015.
De Gregorio, L., Callegari, M., Mazzoli, P., Bagli, S., Broccoli, D., Pistocchi, A., and Notarnicola, C.: Operational Streamflow Forecasting with Support Vector Regression Technique Applied to Alpine Catchments: Results, Advantages, Limits and Lesson Learned, Water Resour. Manag., 32, 229–242, https://doi.org/10.1007/s11269-017-1806-3, 2018.
Gagolewski, M.: stringi: Character String Processing Facilities, R package version 1.2.2, available at: https://CRAN.R-project.org/package=stringi (last access: 15 August 2018), 2018.
Grolemund, G. and Wickham, H.: Dates and Times Made Easy with lubridate, J. Stat. Softw., 40, https://doi.org/10.18637/jss.v040.i03, 2011.
Fraley, C., Leisch, F., Maechler, M., Reisen, V., and Lemonte, A.: fracdiff: Fractionally differenced ARIMA aka ARFIMA(p,d,q) models, R package version 1.4-2, available at: https://CRAN.R-project.org/package=fracdiff (last access: 15 August 2018), 2012.
Hong, T. and Fan, S.: Probabilistic electric load forecasting: A tutorial review, Int. J. Forecasting, 32, 914–938, https://doi.org/10.1016/j.ijforecast.2015.11.011, 2016.
Hyndman, R. J. and Athanasopoulos, G.: Forecasting: principles and practice, available at: https://www.otexts.org/fpp (last access: 15 August 2018), 2018.
Hyndman, R. J. and Khandakar, Y.: Automatic time series forecasting: the forecast package for R, J. Stat. Softw., 27, 1–22, https://doi.org/10.18637/jss.v027.i03, 2008.
Hyndman, R., Athanasopoulos, G., Bergmeir, C., Caceres, G., Chhay, L., O'Hara-Wild, M., Petropoulos, F., Razbash, S., Wang, E., Yasmeen, F., R Core Team, Ihaka, R., Reid, D., Shaub, D., Tang, Y., and Zhou, Z.: forecast: Forecasting functions for time series and linear models, R package version 8.3, available at: https://cran.r-project.org/web/packages/forecast/index.html (last access: 15 August 2018), 2018.
Koutsoyiannis, D., Yao, H., and Georgakakos, A.: Medium-range flow prediction for the Nile: a comparison of stochastic and deterministic methods, Hydrolog. Sci. J., 53, 142–164, https://doi.org/10.1623/hysj.53.1.142, 2008.
Newman, A. J., Sampson, K., Clark, M. P., Bock, A., Viger, R. J., and Blodgett, D.: A large-sample watershed-scale hydrometeorological dataset for the contiguous USA, UCAR/NCAR, Boulder, CO, https://doi.org/10.5065/D6MW2F4D, 2014.
Newman, A. J., Clark, M. P., Sampson, K., Wood, A., Hay, L. E., Bock, A., Viger, R. J., Blodgett, D., Brekke, L., Arnold, J. R., Hopson, T., and Duan, Q.: Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: data set characteristics and assessment of regional variability in hydrologic model performance, Hydrol. Earth Syst. Sci., 19, 209–223, https://doi.org/10.5194/hess-19-209-2015, 2015.
Papacharalampous, G., Tyralis, H., and Koutsoyiannis, D.: Error evolution in multi-step ahead streamflow forecasting for the operation of hydropower reservoirs, Preprints, 2017100129, https://doi.org/10.20944/preprints201710.0129.v1, 2017a.
Papacharalampous, G., Tyralis, H., and Koutsoyiannis, D.: Forecasting of geophysical processes using stochastic and machine learning algorithms, Eur. Water, 59, 161–168, 2017b.
Papacharalampous, G., Tyralis, H., and Koutsoyiannis, D.: Comparison of stochastic and machine learning methods for multi-step ahead forecasting of hydrological processes, Preprints, 2017100133, https://doi.org/10.20944/preprints201710.0133.v2, 2018a.
Papacharalampous, G., Tyralis, H., and Koutsoyiannis, D.: One-step ahead forecasting of geophysical processes within a purely statistical framework, Geosci. Lett., 5, 12, https://doi.org/10.1186/s40562-018-0111-1, 2018b.
Papacharalampous, G., Tyralis, H., and Koutsoyiannis, D.: Predictability of monthly temperature and precipitation using automatic time series forecasting methods, Acta Geophys., 66, 807–831, https://doi.org/10.1007/s11600-018-0120-7, 2018c.
R Core Team: R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.R-project.org/ (last access: 15 August 2018), 2018.
Schaake, J., Cong, S., and Duan, Q.: US MOPEX data set, IAHS-AISH P., 307, 9–28, 2006.
Silveira, C. S., Alexandre, A. M. B., Souza Filho, F. A., Junior, V., and Cabral, S. L.: Monthly streamflow forecast for National Interconnected System (NIS) using Periodic Auto-regressive Endogenous Models (PAR) and Exogenous (PARX) with climate information, RBRH, Porto Alegre, 22, e30, https://doi.org/10.1590/2318-0331.011715186, 2017.
Spinu, V., Grolemund, G., and Wickham, H.: lubridate: Make Dealing with Dates a Little Easier, R package version 1.7.4, available at: https://CRAN.R-project.org/package=lubridate (last access: 15 August 2018), 2018.
Sun, A. Y., Wang, D., and Xu, X.: Monthly streamflow forecasting using Gaussian Process Regression, J. Hydrol., 511, 72–81, https://doi.org/10.1016/j.jhydrol.2014.01.023, 2014.
Taylor, S. J. and Letham, B.: prophet: Automatic Forecasting Procedure, R package version 0.2, available at: https://CRAN.R-project.org/package=prophet (last access: 15 August 2018), 2017.
Taylor, S. J. and Letham, B.: Forecasting at scale, Am. Stat., 72, 37–45, https://doi.org/10.1080/00031305.2017.1380080, 2018.
Thornton, P. E., Thornton, M. M., Mayer, B. W., Wilhelmi, N., Wei, Y., Devarakonda, R., and Cook, R. B.: Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 2, ORNL DAAC, Oak Ridge, Tennessee, USA, https://doi.org/10.3334/ORNLDAAC/1219, 2014.
Tyralis, H.: HKprocess: Hurst-Kolmogorov Process, R package version 0.0-2, available at: https://CRAN.R-project.org/package=HKprocess (last access: 15 August 2018), 2016.
Tyralis, H. and Koutsoyiannis, D.: Simultaneous estimation of the parameters of the Hurst–Kolmogorov stochastic process, Stoch. Env. Res. Risk A., 25, 21–33, https://doi.org/10.1007/s00477-010-0408-x, 2011.
Tyralis, H. and Koutsoyiannis, D.: A Bayesian statistical model for deriving the predictive distribution of hydroclimatic variables, Clim. Dynam., 42, 2867–2883, https://doi.org/10.1007/s00382-013-1804-y, 2014.
Tyralis, H. and Papacharalampous, G.: Variable selection in time series forecasting using random forests, Algorithms, 10, 114, https://doi.org/10.3390/a10040114, 2017.
Tyralis, H., Dimitriadis, P., Koutsoyiannis, D., O'Connell, P. E., Tzouka, K., and Iliopoulou, T.: On the long-range dependence properties of annual precipitation using a global network of instrumental measurements, Adv. Water Resour., 111, 301–318, https://doi.org/10.1016/j.advwatres.2017.11.010, 2018.
Warnes, G. R., Bolker, B., Gorjanc, G., Grothendieck, G., Korosec, A., Lumley, T., MacQueen, D., Magnusson, A., and Rogers, J.: gdata: Various R Programming Tools for Data Manipulation, R package version 2.18.0, available at: https://CRAN.R-project.org/package=gdata (last access: 15 August 2018), 2017.
Wickham, H.: ggplot2, Springer International Publishing, https://doi.org/10.1007/978-3-319-24277-4, 2016.
Wickham, H. and Chang, W.: ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics, R package version 2.2.1, available at: https://CRAN.R-project.org/package=ggplot2 (last access: 15 August 2018), 2016.
Wickham, H. and Chang, W.: devtools: Tools to Make Developing R Packages Easier, R package version 1.13.4, available at: https://CRAN.R-project.org/package=devtools (last access: 15 August 2018), 2018.
Wickham, H., Hester, J., and Francois, R.: readr: Read Rectangular Text Data, R package version 1.1.1, available at: https://CRAN.R-project.org/package=readr (last access: 15 August 2018), 2017.
Wolpert, D. H.: The lack of a priori distinctions between learning algorithms, Neural Comput., 8, 1341–1390, https://doi.org/10.1162/neco.1996.8.7.1341, 1996.
Xie, Y.: knitr: A Comprehensive Tool for Reproducible Research in R, in: Implementing Reproducible Computational Research, Chapman and Hall/CRC, 2014.
Xie, Y.: Dynamic Documents with R and knitr, 2nd Edn., Chapman and Hall/CRC, 2015.
Xie, Y.: knitr: A General-Purpose Package for Dynamic Report Generation in R, R package version 1.20, available at: https://CRAN.R-project.org/package=knitr (last access: 15 August 2018), 2018.
Yang, T., Asanjan, A. A., Welles, E., Gao, X., Sorooshian, S., and Liu, X.: Developing reservoir monthly inflow forecasts using artificial intelligence and climate phenomenon information, Water Resour. Res., 53, 2786–2812, https://doi.org/10.1002/2017WR020482, 2017.
Zeileis, A. and Grothendieck, G.: zoo: S3 infrastructure for regular and irregular time series, J. Stat. Softw., 14, https://doi.org/10.18637/jss.v014.i06, 2005.
Zeileis, A., Grothendieck, G., and Ryan, J. A.: zoo: S3 Infrastructure for Regular and Irregular Time Series (Z's Ordered Observations), R package version 1.8-1, available at: https://CRAN.R-project.org/package=zoo (last access: 15 August 2018), 2018.