Flow channelling and variability in transit times and tortuosity in a fractured rock model with small scale heterogeneity

Transit times and tortuosity for advective particles following water flow in a three-dimensional discrete fracture network with high-resolution representation of internal fracture heterogeneity in aperture is investigated using a numerical model with a stochastic Lagrangian transport framework. The fracture network properties are obtained from field measurements and data of a deep fractured rock formation in the Forsmark site in Sweden. Different assumptions for describing the variance and correlation length used for internal heterogeneity of fracture aperture fields are considered. It is shown that cases with strong variance and correlation length cause earlier first arrivals and delayed late arrivals, thereby extending the range of the transit time breakthrough distribution, compared to the assumption of constant fracture aperture. Also, the timing of peak mass arrival is delayed and its density is reduced. Furthermore, a strong correlation between transit time and tortuosity which occurs for early and bulk mass arrival is revealed, which breaks down for late mass arrival. Thereby two transport regimes are identified, where a first regime is mainly controlled by the network structure and exhibits strong correlation with tortuosity, and a second regime is mainly controlled by the fracture aperture heterogeneity and exhibits weak correlation with tortuosity.

1 Introduction

Understanding fluid flow in fractured crystalline rock is important for a range of geoengineering applications related to managing waste and unwanted substances from energy production, including subsurface geological storage of spent nuclear fuel and carbon sequestration (Matter and Kelemen, 2009; Neretnieks, 1993; Randolph and Saar, 2011; Tsang et al., 2015; Tsang and Niemi, 2013). Central to the study of fluid flow in fractured rock is the representation of heterogeneity exhibited by fractures and fracture networks which vary at a multitude of scales (Davy et al., 2010; de Dreuzy et al., 2012; Maillot et al., 2016; Neuman, 2005; Pyrak-Nolte et al., 1992; Zimmerman and Bodvarsson, 1996). For modelling sparsely fractured crystalline rock, a common approach is to assume flow only occurs in fracture surfaces embedded in an impermeable rock matrix, and therefore the representation of fractures and their geometrical and hydrological properties is essential. A stochastic approach is typically employed where multiple fractures are sampled as planar surfaces, typically as discs or polygons, following distributions describing intensity, strike, dip, orientation, length and transmissivity, which combined form a network of connected fractures (Cacas et al., 1990; Frampton and Cvetkovic, 2011; Outters, 2003; Selroos et al., 2002; Selroos and Follin, 2014). Direct measurement of fracture surface roughness and variable aperture is cumbersome and usually involves observation of trace profiles on rock outcrops (Candela et al., 2009; Magsipoc et al., 2020). However, effective transmissivity or permeability of a section of bedrock, consisting of multiple fractures in a network, can be obtained through inverse modelling of hydraulic pressure tests in boreholes (Follin and Hartley, 2014; Frampton and Cvetkovic, 2010). Therefore, numerical discrete fracture network (DFN) models of sparsely fracture rock often employ an assumption of effectively homogeneous properties at the scale of individual fractures, corresponding to an assumption of effectively constant aperture in the fracture plane.

However, real-world fractures have rough surfaces and significant variability in aperture which can impact water flow and transport of solutes (Brown, 1987; Hakami and Barton, 1991). Several studies covering a range of different rock types indicate fracture surface roughness may follow self-affine scaling properties (Brown, 1987; Glover et al., 1998; Houben et al., 2024; Ogilvie et al., 2003; Power and Tullis, 1991; Renard et al., 2006). However, the fracture void space between adjacent rough surfaces does not necessarily follow the same scaling behaviour, and observations based on sample measurements indicate fracture aperture fields may be described by normal or lognormal distributions (Hakami, 1995; Johns et al., 1993; Keller, 1998; Thörn et al., 2015; Thörn and Fransson, 2015; Watanabe et al., 2008). Although it is known that internal variability controls flow channelling at the scale of single fractures (Detwiler and Rajaram, 2007; Johnson et al., 2006; Liu et al., 2018; Moreno et al., 1988) and generic networks (Nordqvist et al., 1992), there is still limited understanding of effects at the bedrock scale of fractures forming large scale complex networks. Studies have identified network structure to exert more control on transport than internal variability in large domains, but the effect also depends on the assumptions made for describing fracture heterogeneity (Frampton et al., 2019; Hyman et al., 2021; Makedonska et al., 2016). Fracture surface roughness and variable aperture also plays a significant role on mechanical deformations which greatly influences flow (Kwon and Min, 2021; Watanabe et al., 2009). It is therefore highly relevant to understand how internal fracture aperture heterogeneity impacts water flow and advective particle transit times in order to make appropriate decisions on how to adequately represent fractures in discrete fracture network models.

In this study, a model experiment is set up to investigate the impact of internal fracture aperture heterogeneity on flow and transport in a model configured according to fracture set distributions obtained from the Forsmark site investigation in Sweden. The representation of internal aperture heterogeneity is based on an assumption of lognormally distributed apertures in the fracture plane which is consistent with observations reported in the literature. Thereby, the aim is to investigate to what extent the variance and correlation length of aperture fields used for representing internal fracture variability impacts flow channelling by advective particle transit times and tortuosity in a realistic discrete fracture network. The underlying assumption is that for aperture fields with small variance and short correlation lengths, the impact of internal fracture heterogeneity on transit times and pathway tortuosity is negligible, and a constant effective fracture aperture can be assumed. However, if strong variance and large correlation lengths are imposed on fractures in the network, the impact on transit times and tortuosity is not negligible.

2 Method

The procedure employed follows the methodology developed by Frampton et al. (2019) for investigating transit times in discrete fracture networks with internal aperture heterogeneity. Here, only Gaussian textures for fracture heterogeneity are considered, which corresponds to lognormal distributions for fracture aperture fields. Also, a large-scale DFN realisation is considered which is based on the well-characterised Forsmark site in Sweden, using fracture statistical properties at the depth interval of 200–400 m of the sparsely fractured rock formation FFM01 (Follin et al., 2007). Thus, this study is based on site-specific properties instead of synthetic generic properties. Also, impacts on pathway length and tortuosity are investigated. Fractures are represented as two-dimensional surfaces with assigned aperture within an impermeable three-dimensional domain representing the host bedrock (Fig. 1). Pressure boundary conditions are assigned to model inflow and outflow boundaries, at $x=-\mathrm{50}$ m and x=50 m respectively, yielding steady-state flow through the fracture network. Particle tracking is then conducted following the flow field through the network.

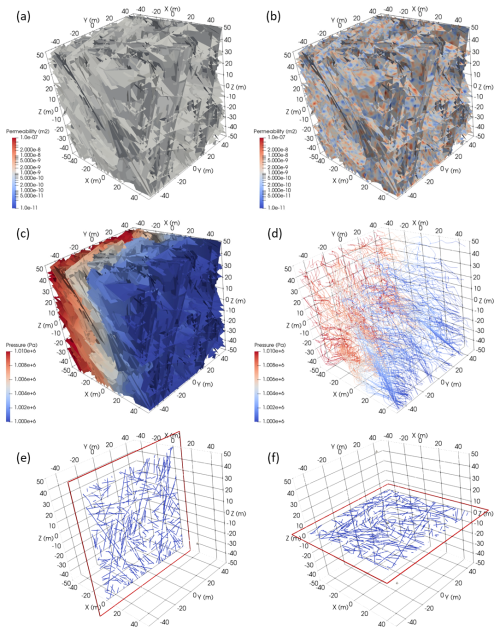
Figure 1 The discrete fracture network model in a $\mathrm{100}\times \mathrm{100}\times \mathrm{100}$ m³ domain. (a) Reference case with constant aperture. (b) Case with large variance and correlation length. (c) Pressure solution for the reference case. (d) Particle trajectories for the reference case, only 300 are shown for visibility. Slices through the domain at the origin with (e) normal in the x direction and (f) normal in the z direction showing fracture traces.

Particle tracking is used to represent transport of waterborne substances, such as solutes and dissolved contaminants. A stochastic Lagrangian approach is employed (Cvetkovic et al., 1998, 1999; Cvetkovic and Dagan, 1994; Frampton and Cvetkovic, 2007), where inert particles that follow the flow field through the DFN represent the advective and dispersive spreading of a plume through the heterogenous domain. The transit travel time τ experienced by a particle along its trajectory s from source r_s to sink r_t is

$$\begin{array}{}\text{(1)}& \mathit{\tau }=\underset{s=r_s}{\overset{r_t}{\int }}{\displaystyle \frac{\mathrm{1}}{v\left(s\right)}}\mathrm{d}s\end{array}$$

where v is fluid velocity. Pathway tortuosity is then

$$\begin{array}{}\text{(2)}& \mathit{\lambda }={\displaystyle \frac{\mathrm{1}}{r_t-r_s}}\underset{s=r_s}{\overset{r_t}{\int }}\mathrm{d}s\end{array}$$

where $L=r_t-r_s$ is a straight-line path through the length of domain in the net flow direction. For a numerical DFN model with a discretized mesh, the trajectory can be seen as a random walk through the fracture network consisting of N discrete steps along segments i, where each segment has velocity v_i and length r_i so that particle transit time becomes

$$\begin{array}{}\text{(3)}& \mathit{\tau }=\sum _{i=\mathrm{1}}^N{\displaystyle \frac{r_i}{v_i}}\end{array}$$

and pathway tortuosity becomes

$$\begin{array}{}\text{(4)}& \mathit{\lambda }={\displaystyle \frac{\mathrm{1}}{L}}\sum _{i=\mathrm{1}}^N{r}_i\end{array}$$

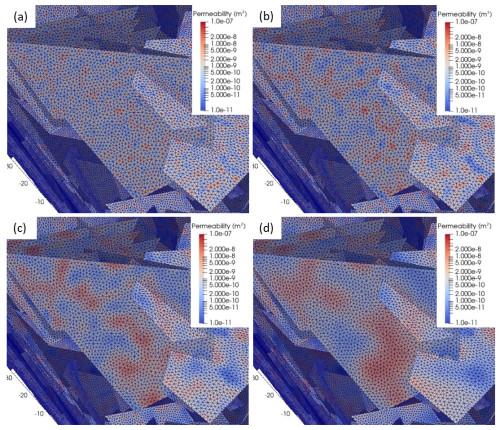
The simulation cases investigated are as follows. First, a reference case DFN model is generated where fractures have a constant aperture of 0.1 mm, which corresponds to a permeability of about $\mathrm{8.3}\times {\mathrm{10}}^{-\mathrm{10}}$ m² using the cubic law (Witherspoon et al., 1980; Zimmerman and Yeo, 2000). The DFN is solved for flow followed by advective particle tracking. Then, the same geometric DFN is used but where each fracture is assigned a heterogenous aperture field, which is then solved for flow and followed by particle tracking. The cases with heterogeneous aperture fields always have a mean aperture of 0.1 mm, but with different variance and correlation lengths. Both low variance (0.1) and high variance (0.3) cases are considered, together with correlation length factors of 0.1, 0.2, 0.5 and 1. The correlation length factors are relative to the lower truncation limit of the fracture size distribution of the DFN, which is 5 m in length scale; hence the corresponding correlation lengths are 0.5, 1, 2.5 and 5 m.

Thus, a reference case DFN with constant fractures and eight cases of the DFN with heterogeneous fractures are computed, yielding a total of nine flow simulations. Each flow simulation is injected with about 10 000 particles, which are uniformly distributed along the fracture transects intersecting the inflow boundary plane. The analysis is based on the transit times and pathway tortuosity experienced by the particles as they follow advective water flow through the network from the injection plane at $x=-\mathrm{50}$ m to the outflow plane at x=50 m. The dfnWorks computational suite (Hyman et al., 2015) is used to generate the fracture network, solve for flow, and conduct particle tracking.

The DFN model domain is $\mathrm{100}\times \mathrm{100}\times \mathrm{100}$ m³ and contains fractures with a length scale from 5 m and larger, following a power-law size distribution (Follin et al., 2007; Tables 11–20). The mesh resolution is set to constant at 0.5 m, in order to accurately resolve even the smallest fractures with a variable permeability field and without incurring excessive computational cost for the entire DFN. The smallest correlation length corresponds to variability at the mesh scale resolution, representing high frequency variability in aperture with essentially random internal structure. The largest scale correlation corresponds to the size of the smallest fractures, thus representing strong internal structure.

The reference case DFN is shown in Fig. 1a, and the case with large variance and correlation length is shown in Fig. 1b. The computed pressure field is shown in Fig. 1c, and about 300 particle trajectories are shown in Fig. 1d. The fracture network is based on site data from a very sparsely fractured rock formation, which is more clearly visualised by slices through the domain as shown in Fig. 1e, f. A zoomed detail of a selected part of the DFN depicting the mesh for a few fractures and fracture intersections with the four cases of systematically increasing correlation length is shown in Fig. 2.

Figure 2 Detail of the DFN showing the mesh with internal fracture variability for the cases with correlation length (a) 0.5 m, (b) 1.0 m, (c) 2.5 m, and (d) 5.0 m with variance 0.3.

3 Results and discussion

Considering the reference case with constant fracture aperture, the arrival time density distribution for particle transit times exhibits a distinct peak at around 10⁻¹ yr, and with several secondary and higher order modes for later times (Fig. 3, black). The entire distribution spans about seven orders of magnitude from first arrival at about 10⁻² yr to last arrival at about 10⁵ yr. The low variance cases have a similar spread in arrival times as the reference case, despite increasing correlation lengths (Fig. 3a), but the high variance cases can reach times over 10⁶ yr and hence span over eight orders of magnitude, depending on correlation length (Fig. 2b). Note however, the density of the first mode (i.e., peak) which occurs near transit time 10⁻¹ yr is reduced as correlation length increases, slightly for low variance cases from about 1.0 for the short correlation length case Corr 0.1 (Fig. 3a, dotted cyan) to about 0.9 for the long correlation length case Corr 1.0 (Fig. 2a, dashed red), but more notably for the high variance cases from about 1.0 to 0.7, for the same correlation length cases (Fig. 3b). Thus, the main effect of correlation length is to reduce the density of particles around the first mode, i.e., the peak arrival time. The increased correlation lengths also alter the timing of the peak, as well as the timing and spread of the secondary and higher order modes. Furthermore, the increased correlation lengths generally increase the spread of transit times, increasing the density of particles for first and early arrivals, prior to the first mode, as well as the density of the secondary and higher order modes in the tails of the distribution.

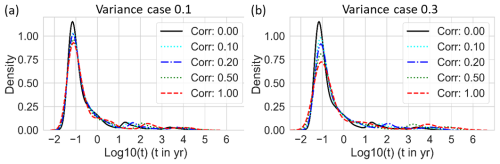
Figure 3 Density distribution of the logarithm of particle transit times through the domain for the reference case (Corr 0, black) and increasing correlation length cases 0.1 (dotted cyan), 0.2 (dash-dotted blue), 0.5 (dotted green), and 1 (dashed red) with (a) variance case 0.1 and (b) variance case 0.3.

The differences in arrival time are also apparent by inspecting the corresponding cumulative density distributions (Fig. 4). For small variance, the cumulative densities for increasing correlation lengths are slightly shifted towards later arrival times (Fig. 4a). The high variance cases exhibit more distinguished shifts towards later times and with greater spread as correlation length increases (Fig. 4b). The density of first arrivals at around 10⁻² yr are visibly increased for the high variance cases (Fig. 4b). Also, the cumulative density of arrivals is notably shifted towards later times.

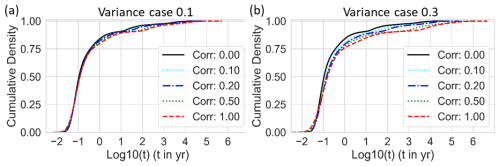
Figure 4 Cumulative density distribution of the logarithm of particle transit times through the domain for the reference case (Corr 0, black) and increasing correlation length cases 0.1 (dotted cyan), 0.2 (dash-dotted blue), 0.5 (dotted green), and 1 (dashed red) with (a) variance case 0.1 and (b) variance case 0.3.

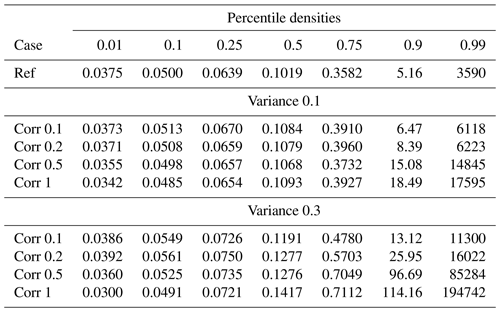
The median transit times (0.5 percentile density) are not significantly affected by correlation length for the low variance cases (Fig. 5a, blue dots) and exhibit slight increase for the high variance cases (Fig. 5b, blue dots). However, first and early arrivals exhibit shorter transit times for both low and high variance cases, which is mainly evident for the low percentile densities, below 0.1, corresponding to less than 1 % of the total particles injected. A more significant reduction in transit time is observed for the 0.001 percentile, corresponding to 0.1 % of the total particle mass. Interestingly, the low variance cases exhibit an approximate linear reduction in transit times as correlation length increases for small percentiles, but the high variance cases exhibit a slight rise for correlation length factors 0.1 and 0.2, before a reduction in transit time for correlation factors 0.5 and 1.0. Similar nonlinear responses to changes in correlation length for small percentiles of transit times have been observed for synthetic DFN models comprising small networks (Frampton et al., 2019).

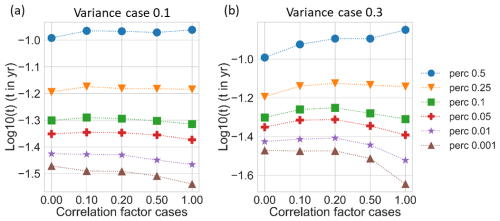
Figure 5 Percentiles of the logarithm of particle transit times for the reference case and the cases with increasing correlation length factor with (a) variance case 0.1 and (b) variance case 0.3.

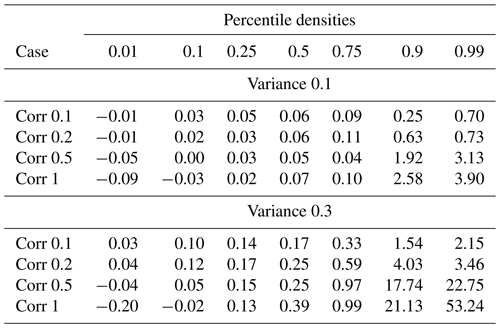
The transit time for the first 1 % particle arrivals (0.01 percentile) for the large variance case with maximum correlation length factor (Corr 1.0) is 0.03 yr, which can be compared to the constant reference case which is 0.0375 yr (Table 1). Thus, the relative difference is a 20 % reduction in transit time for the first 1 % of particle mass arrival for this case compared to the reference case (Table 2). Similarly, considering the first 10 % of particle arrivals (0.1 percentile) for the large variance and maximum correlation case, the relative difference is only a 2 % reduction in transit time. However, considering the first 50 % (0.5 percentile) of particles arrivals, the relative difference is a 39 % increase in transit time, and considering 90 % (0.9 percentile) and 99 % (0.99 percentile) of arrivals, the relative increase is a factor of 21 and 53 respectively. Most simulation cases exhibit later arrivals for percentiles above 0.1 and all cases for percentiles above 0.25. Thus, there is a transition between reduction (negative relative differences) and increase (positive relative differences) in transit time which is caused by introducing fracture aperture heterogeneity, and the transition point depends both on the variance and correlation length of the aperture field employed. For the cases with small variance, all correlation lengths cause reduced transit time for 1 % particle density (0.1 percentile) and below. The transition occurs for greater densities, between 1 % and 10 % for all correlation lengths except the maximum (Corr factor 1.0) which still exhibits reduced transit time at 10 % density (0.1 percentile). For the cases with large variance however, only the larger correlation lengths (Corr factor 0.5 and 1.0) cause reduced transit times for 1 % particle density and below. The reduction is still seen at the 10 % density for the maximum correlation length. The precise point of transition for each correlation length could be obtained by studying additional percentiles in the range 0.01 and 0.1. Also, as before, a nonlinear behaviour is seen for the changes in transit time as correlation length increases for the high variance cases (cf. Fig. 5b) which is not apparent for the low variance cases (cf. Fig. 5a).

Table 1 Transit times (yr) for different percentile densities.

Table 2 Relative difference in transit times with respect to reference case (–).

Particle tortuosity is calculated as the ratio of path length over domain distance (100 m) and quantifies increase in path length relative to a straight lateral line through the domain, from the injection plane to the outflow plane. The reference case exhibits a spread in tortuosity from just above 1 to almost 3, with median particle mass (0.5 percentile) exhibiting a tortuosity just below 1.5 (Fig. 6). Considering the low variance cases with increasing correlation length (Fig. 6a), tortuosity remains relatively constant for the bulk particle mass, as the median and interquartile range remains essentially unchanged. The high variance cases exhibit an increase in tortuosity, seen by the increase in median and interquartile range as well as outliers, as correlation length increases (Fig. 6b). Interestingly, there is an apparent peak in tortuosity for correlation length factors 0.2 and 0.5, seen by the increased tortuosity of the outliers, which reduces slightly for the correlation length factor 1.0 Thus, here also a nonlinear behaviour is seen as correlation length increases for the high variance cases only.

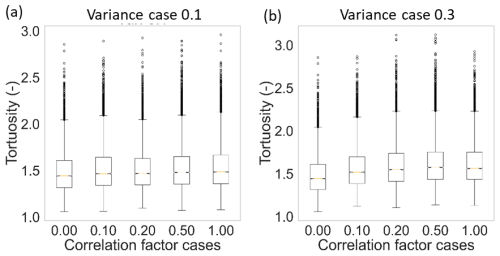
Figure 6 Boxplots showing the median, interquartile range, whiskers and outliers of particle pathway tortuosity for the reference case and the cases with increasing correlation length factor with (a) variance case 0.1 and (b) variance case 0.3.

Tortuosity is strongly correlated to transit time for the reference case considering the bulk particle mass, corresponding to first and median arrivals, from about 10⁻² to 10⁰ yr (Fig. 7a). Late arrivals with transit times around 10⁰ yr and greater, corresponding to higher order modes and the tail of the distribution, do not exhibit any clear correlation with tortuosity which remains around 1.7 with significant spread. The case with largest variance and correlation length factor exhibits greater spread in both arrival times and tortuosity (Fig. 7b). The strong correlation for small transit times between 10⁻² to 10⁰ yr is still apparent but with greater spread, indicating the correlation is weaker. Also, although the particle density is increased for the higher modes with transit time above 10⁰ yr, there is no apparent correlation with tortuosity. Most of the late particles still have a tortuosity around 1.7 but with more significant spread.

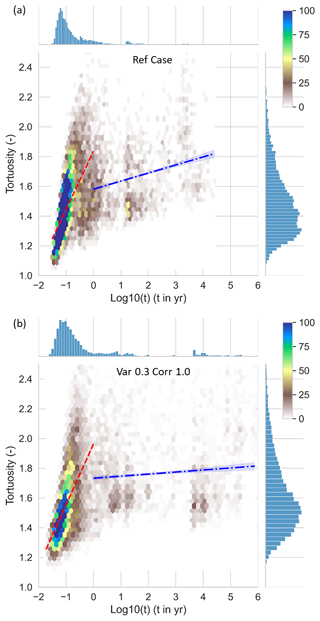
Figure 7 Joint density distribution and correlation between particle pathway tortuosity and transit time for (a) the reference case and (b) the case with large variance 0.3 and large correlation length factor 1.0. The lines in each plot corresponds to a linear regression for transit times below 10⁰ yr (dashed red), and above 10⁰ yr (dash-dotted blue).

The reference case shows the particle behaviour under the assumption of constant fracture aperture in the network. Thus, the tortuosity exhibited by the reference case (Fig. 7a) is controlled solely by the connectivity between fractures in the network, is the large scale structure. When internal fracture aperture heterogeneity is employed, tortuosity generally increases (Fig. 7b) for the bulk particle mass arrivals. Although the late arrivals which exist in the reference case become delayed when considering internal variability, the delay is not caused by a significant increase in path length. Only a small increase in path length occurs despite a significant delay in transit time, as seen by the increased spread and scatter in Fig. 7b. This implies the fracture network is subject to two transport regimes. A first regime for the bulk particle mass arrivals which exhibits strong correlation between tortuosity and transit time, indicating path length through the network exhibits relatively strong control over transit time. The second regime consisting of the tails of the distribution contain very slow pathways, but without a significant increase or otherwise notable change in path length. Thus, the slow transport regime is associated with other factors than path length, such as locally reduced apertures, causing slow flow and delay in transport. Hence, fracture aperture heterogeneity causes an increased density of particles with long transit time, and acts to reduce the strong correlation with tortuosity in the fast transport regime (illustrated by the dashed red regression lines in Fig. 7), and simultaneously increases the weak correlation with tortuosity in the slow transport regime (dash-dotted blue regression lines in Fig. 7).

4 Conclusions

This study investigates effects of internal fracture aperture heterogeneity on flow and transport by particle transit times in a discrete fracture network model based on site-specific bedrock data. The fracture network properties are obtained from Forsmark in Sweden, which is the planned site for the construction of the subsurface repository for spent nuclear fuel, and the host geological formation consists of very sparsely fractured crystalline rock. The main control on transit times is evidently the fracture network, which governs the overall form of the arrival time distribution and its first mode (main peak) in transit time and tortuosity. Imposing fracture aperture heterogeneity changes the timing and density of the peak transit time such that it is slightly delayed and the density is reduced. Higher order modes and their transit times are more significantly influenced by aperture heterogeneity and their timing are generally delayed. Also, an increase in the total range of transit times is observed, causing both earlier first arrivals and delayed late arrivals, corresponding to the extremes of the distributions, which can prolong the tails of transit time by orders of magnitude. Both early and late arrivals are important for applications. An increase in early arrivals is important for safety assessment of subsurface repositories, in order to quantify first-incident exposure risks. Late arrivals are important to understand long-term effects of contaminant sources and legacy sites, such as mines and other subsurface pollutant sources.

Based on the discrete fracture network model and simulation cases considered in this study, the fracture aperture field with high variance and strong correlation (variance case 0.3, correlation length factor 1.0) can cause the first 1 % of particle mass to arrive about 20 % earlier than if a constant fracture aperture field is assumed. Considering the median density, i.e., 50 % mass, particles can arrive about 40 % later than expected. The transition between earlier to delayed arrivals by introducing fractures with heterogeneous aperture fields occurs at small percentiles of the arrival time distribution. For the cases with small variance in the aperture field, this transition is approximately linear with correlation length, and occurs between 1 % and 10 % of particle mass. For the cases with large variance, this transition is not linear and occurs at about 1 % of particle mass for strongest correlation lengths.

Accounting for internal heterogeneity incurs an additional computation cost because a higher resolution mesh is needed to resolve the fractures in the network. However, the effects on particle transit times can in principle be obtained from simulations with constant aperture or permeability by adjusting the densities of early and late arrivals by a certain amount in a post-processing stage. The amount that needs adjusting will likely depend on both fracture and network properties, but can be estimated from a limited set of simulations where variable aperture is accounted for. For this discrete fracture network, assuming the strongest variance and correlation length case correspond to a worst-case scenario, conservative estimates of first-incident exposure risk can still be obtained from the constant aperture transit time distribution by allowing the first 1 % of mass to arrive 20 % earlier. Although these specific changes in density on the travel time distribution cannot be generalised to other sites with different rock formations and fracture network properties, it seems plausible that internal fracture variability will have some non-negligible impact on early and late arrivals. The effect is likely a balance between the strength of the internal fracture correlation structures and the overall network structure. This highlights the need for further measurements and analysis of internal fracture variability using rock samples and in situ observations.

The effects of internal fracture aperture heterogeneity are also evident by its impacts on particle path lengths and tortuosity. When internal aperture heterogeneity is considered, path length and tortuosity is increased. The increase occurs for all transit times. Based on analysis of correlation between tortuosity and transit time, two transport regimes are identified for this fracture network. The first regime corresponds to the bulk particle mass with short transit times and exhibits strong correlation with tortuosity. The second corresponds to long transit times and exhibits weak correlation with tortuosity. Fracture aperture heterogeneity causes an increased density of particles with long transit time and further weakens the correlation with tortuosity, indicating path length is not a significant contributing factor for late arrivals. Instead, fracture aperture heterogeneity which slows down flow velocity locally plays a more significant role on controlling late time arrivals in the tails of the transit time distribution.