Large-scale reservoir modeling of the Vendenheim geothermal site (France)

During the Vendenheim deep geothermal project (Strasbourg Eurometropole, France), large induced seismic events led to the arrest of the project. Two important features of the induced seismicity were unexpected: the large distance to the wells of a cluster of seismic events (4–5 km) and the occurrence of the largest event Mlv3. 9 at the bottom of the wells, six months after shut-in. To better understand the natural hydro-thermal conditions at the Vendenheim site, we develop within the framework of the DT-GEO project (Horizon Europe) a simplified large-scale model (8 km × 8 km × 6 km) of the area. We aim at performing in-silico experimentation to reproduce the natural hydrothermal state of the geothermal reservoir related to the heat flow (conductive/convective) within the model. We first test our methods by solving 2D and 3D benchmarks related to the convective regime in saturated porous media. Our model is based on the MOOSE/GOLEM framework (finite element approach) and integrate the public regional geological model GEORG that includes major lithologies. We present the coarse-grained simulations of the natural fluid circulation.

1 Introduction

The Vendenheim geothermal site is situated in the Upper Rhine Graben region (URG), which is located in the Rhine valley between the Vosges and the Black Forest mountains, in borders of France and Germany, and in the north of Switzerland. The URG is one of the promising regions for geothermal exploration in the European context (Frey et al., 2022). However, it has been studied and verified that in the context of geothermal systems, induced seismicity could be generated, causing many projects to be abandoned, (Majer et al., 2007; Zang et al., 2014; Kwiatek et al., 2019; Gaucher et al., 2015; Schmittbuhl et al., 2021). This was the case of the Geoven project that was developed in the Vendenheim area, in the north of Strasbourg France. This project was closed due to a series of earthquakes between March 2018 and June 2021, in which the largest event had a magnitude of M_Lv 3.6 (Schmittbuhl et al., 2021).

For this reason, as part of the Digital Twin for GEOphysical Extremes (DT-GEO) project (https://dtgeo.eu, last access: 4 October 2024), we develop a 3D Thermal Hydrological coupled (TH) modelling to compute the hydrothermal flow with a temperature dependent density and viscosity rheology, in a porous medium, using the MOOSE/GOLEM application (Jacquey and Cacace, 2017; Giudicelli et al., 2024), in order to verify if a hydrothermal convective system is compatible with known observations at the Vendenheim site. Furthermore, we aim to get a better idea of the initial conditions of a model for induced seismicity, as this hydrothermal convection could introduce characteristic time and space scales.

We use a simplified structural model based on the GEORG platform (https://maps.geopotenziale.eu, last access: 8 October 2024), within the Vendenheim area (Strasbourg, France) in order to set the distribution of the principal geological layers. In the shallow crust fluid circulation in geological systems, such as: tectonically active systems, ash-flow calderas, sedimentary basins and fault regions, have been shown to exist. These systems may have a rock permeability large enough to allow thermally driven fluid flow (Davaille, 1999; Simms and Garven, 2004; Lopez et al., 2016; Patterson et al., 2018; Duwiquet et al., 2019; Guillou-Frottier et al., 2020). Thermally driven fluid circulation can occur in a variety of systems in Earth's interior (Donaldson, 1970; Schubert et al., 2001; Bataillé et al., 2006; Angiboust et al., 2012).

In the context of geothermal fields as Vendenheim, the geothermal potential of an area, which is based on environmental, technical, economic and acceptance principle according to Bayer et al. (2019), must be estimated by evaluating the temperature field and the mode of heat transfer (Ranalli and Rybach, 2005). In a saturated porous medium heated from below (i.e. higher temperature at depth than at surface), heat transfer is better understood by the Rayleigh number, that indicates the relative importance of the viscous stabilising mechanisms to the buoyancy destabilising mechanisms. The Rayleigh number in porous media is defined according to Schubert and Straus (1979), Nield (1994), Desaive (2003) as:

$$\begin{array}{}\text{(1)}& \mathit{Ra}={\displaystyle \frac{k{\mathit{\rho }}_{\mathrm{f}}{c}_{\mathrm{f}}g\mathit{\beta }(T_{\mathrm{b}}-T_{\mathrm{t}})H}{{\mathit{\lambda }}_{\mathrm{b}}\mathit{\mu }}},\end{array}$$

where k is the intrinsic permeability, ρ_f is the density of the fluid, c_f is the fluid heat capacity, g is the gravity acceleration, β is the fluid thermal expansion, T_b and T_t are the bottom and top temperature respectively, H is the height of the model, λ_b is the bulk heat conductivity, and μ is the fluid viscosity. The critical Rayleigh number (Ra_c) is defined as the value of the Rayleigh number at which instability begins and free convection develops: When Ra>Ra_c, the system is unstable (heat is transferred by convection), and when Ra<Ra_c, the system is stable (heat is transferred by conduction. In porous media we find in the literature that Ra_c=4π² (Lapwood, 1948; Murphy, 1979; Desaive, 2003). Furthermore, thermal convection is controlled by two main processes: an increased pressure gradient (“forced convection”), and buoyancy effects due to temperature-dependent fluid density.

In this context, we found Pola et al. (2020), in which a representative model from NE Italy with low-temperature gradient, was developed, in which thermal convection was observed. Moreover, in Liu et al. (2021), a 3D model with a fracture the type of heat flow was investigated using the Nusselt number. Furthermore in Detournay et al. (2022), they developed a 3D fracture model, where 3 heat transfer mechanisms were considered in a geothermal context. In contrast to these works, here we discuss the Rayleigh number to better understand the heat transfer in the Vendenheim region.

In the following sections we present our methods for TH modeling (Sect. 2). After that, in Sect. 3 we present 2D and 3D benchmarks to test our methods in the context of convective flow. In Sect. 4 we present the simplified model based on the Vendenheim site, with the results of the TH modeling, and discuss the possibility of large-scale natural hydrothermal circulation in the geothermal reservoir. The mechanical consequences of possible thermal anomalies (fault instability) as well as numerical stability (mesh sensitivity) require further analysis and are beyond the scope of this article.

2 Methods

In the following, the governing equations are present, in the context of the Thermal Hydrological coupling (TH). This system is solved by Golem (Jacquey and Cacace, 2017; Cacace and Jacquey, 2017), a Moose-based application (Giudicelli et al., 2024) for modelling coupled-Thermo-Hydro-Mechanical processes in faulted geothermal reservoirs.

First, the equilibrium of fluid mass equation in a non-deformable porous matrix is presented:

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{n}{K_{\mathrm{f}}}}{\displaystyle \frac{\partial p_{\mathrm{f}}}{\partial t}}+\mathrm{\nabla }\cdot {\mathit{q}}_{\mathrm{D}}=\mathrm{0},\end{array}$$

where n is the porosity, K_f represents the fluid bulk modulus, t is the time, and q_D is the Darcy velocity, which is described according to the Darcy's law as:

$$\begin{array}{}\text{(3)}& {\mathit{q}}_{\mathrm{D}}=-{\displaystyle \frac{\mathit{k}}{{\mathit{\mu }}_{\mathrm{f}}}}\cdot (\mathrm{\nabla }{p}_{\mathrm{f}}-{\mathit{\rho }}_{\mathrm{f}}\mathit{g}),\end{array}$$

where k , μ_f, ρ_f, and g represent the permeability tensor, the viscosity and fluid density, and the gravity acceleration respectively.

The temperature distribution is governed by the energy balance equation:

$$\begin{array}{}\text{(4)}& (\mathit{\rho }c{)}_{\mathrm{b}}{\displaystyle \frac{\partial T}{\partial t}}+\mathrm{\nabla }\cdot {\mathit{q}}_T=\mathrm{0},\end{array}$$

where (ρc)_b is the product of the bulk density and heat capacity, and q_T is the heat flux, defined as:

$$\begin{array}{}\text{(5)}& {\mathit{q}}_T={\mathit{\rho }}_{\mathrm{f}}{c}_{\mathrm{f}}{\mathit{q}}_{\mathrm{D}}T-{\mathit{\lambda }}_{\mathrm{b}}\mathrm{\nabla }T,\end{array}$$

where c_f is the specific heat capacity of the fluid and ${\mathit{\lambda }}_{\mathrm{b}}=n{\mathit{\lambda }}_{\mathrm{f}}+(\mathrm{1}-n){\mathit{\lambda }}_{\mathrm{s}}$ is the bulk thermal conductivity, with λ_f and λ_s being the fluid and solid thermal conductivity. The first and second terms correspond to the convective and conductive flux respectively. For further information, we refer to Magnenet et al. (2014), Blöcher et al. (2018), Vallier et al. (2019).

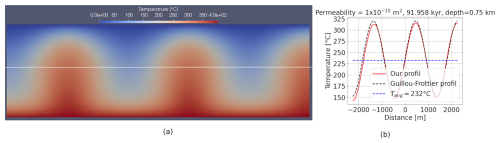
Figure 1 Temperature distribution (a), and horizontal temperature profile (b) for $k=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{15}}$ m² at a depth of 0.75 km. The profile passes through the white line shown in panel (a). The steady state is observed in this example using a tolerance of $\mathrm{1}\times \mathrm{10}-\mathrm{14}$. (See Fig. 1 in Guillou-Frottier et al. (2020). The model is 4.5 km long and 1.5 km in depth.

Table 1 Boundary conditions used in Guillou-Frottier et al. (2020) for the 2D results.

3 2D and 3D thermal convection benchmarks in faulted systems

To validate our methods, we reproduce the benchmarks proposed in Magri et al. (2017) and Guillou-Frottier et al. (2020), where the Elder problem is solved in the context of 2D and 3D hydrothermal convection in fault zones. We restrict our study to the hydrothermal problem, no mechanics are considered.

3.1 2D benchmark

The model dimensions are 1.5 km-thick (z direction) and 4.5 km-wide (x direction), with square elements ($\mathrm{\Delta }z=\mathrm{\Delta }x=\mathrm{20}$ m), having 16 875 elements in total. Fixed temperatures of 0 and 400 °C are imposed in the top and bottom boundary respectively, no temperature flow is considered at the sides. For the pore pressure, no flow is imposed in all boundaries except the top boundary. Here a fixed pressure of 1×10⁵ Pa is imposed. A summary of these conditions is presented in Table 1.

The material properties are reported in Table 2.

Table 2 Values of the physical parameters used to evaluate the convective solution. Porosity values are on a scale from 0 to 1. Permeabilities are isotropic.

Fluid density ρ_f and fluid viscosity μ_f obey the following laws:

$$\begin{array}{ll}{\displaystyle }{\mathit{\rho }}_{\mathrm{f}}\left(T\right)& {\displaystyle }={\mathit{\rho }}_{\mathrm{f}\mathrm{0}}-\mathrm{0.14167}\times T-\mathrm{0.0022381}\times T^{\mathrm{2}}\\ \text{(6)}& {\displaystyle }{\mathit{\mu }}_{\mathrm{f}}\left(T\right)& {\displaystyle }={\mathit{\mu }}_{f\mathrm{0}}\times {\mathrm{10}}^{\frac{\mathrm{247.8}}{T+\mathrm{133}}},\end{array}$$

with T in °C, ρ_f0=1036.6 kg m⁻³, ${\mathit{\mu }}_{\mathrm{f}\mathrm{0}}=\mathrm{2.414}\times {\mathrm{10}}^{-\mathrm{5}}$ Pa s, are the fluid density and viscosity at the top of the model.

We implement these laws using a Golem function that allows us to introduce the variation of density and viscosity with temperature using tables. These tables are elaborated externally by applying the function in the desired temperature range.

We impose initial conditions of $T(t=\mathrm{0})=(T_{\mathrm{b}}-T_{\mathrm{t}})/\mathrm{1500}\cdot z$ (with T_b and T_t being the temperature at the bottom and top of the model), and $p_{\mathrm{f}}(t=\mathrm{0})=\mathit{\rho }gz$. We evaluate the convergence of the system towards the steady state by using the following convergence criteria:

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{u^{n+\mathrm{1}}-u^n}{\mathrm{\Delta }t}}<\mathit{\tau }{u}^{n+\mathrm{1}},\end{array}$$

where u represents the solution of the system, Δt is the time step, the superscript n+1 and n refer to the current and old solutions respectively, and τ is the tolerance ($\mathit{\tau }=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{14}}$ in this case). This equation represents definition of the L2-norm on relative change in the solution between two time steps.

In Fig. 1, we reproduce the 2D results of Guillou-Frottier et al. (2020) (Fig. 1 in that paper) for the permeability $k=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{15}}$ m², in 91.958 kyr at a depth of 0.75 km. The horizontal profile of temperature in the middle of the model (showing by the white line) compared to profile obtained in Guillou-Frottier et al. (2020). The average temperature T_avg (232 °C in this work and 236 °C in theirs), and ΔT, defined as the difference between the maximal and average temperature within the profile, are also very similar (83 °C in this work and 84 °C in theirs). The steady state is reached in our work with a tolerance of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{14}}$.

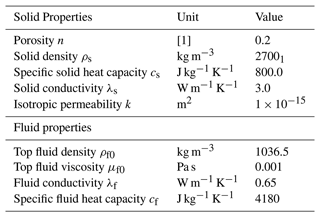
3.1.1 Darcy velocity as a function of the permeability

Keeping the same model, we studied the behavior of the maximum Darcy velocity with respect to different isotropic permeabilities in a range from $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{16}}$ to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{13}}$ m². In Fig. 2 we show the variation of the maximal value of the vertical component of the Darcy velocity with respect to the permeability. The red marks represent the permeability values where convection is observed, while blue marks show the permeability values where convection is not observed. For permeability values where convection develops, we select the maximum Darcy velocity value over time. For permeabilities of $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{16}}$ and $\mathrm{6.25}\times {\mathrm{10}}^{-\mathrm{16}}$ m², convection is not observed, therefore Darcy velocity is very low. We observe that the Darcy velocity increases in the convective regime when the permeability increases. Moreover, for permeability values for which convection is observed, the relationship between permeability and Darcy velocity appears to be linear. This is demonstrated by the dashed line in Fig. 2, which illustrates this relationship and was obtained through linear regression. This can also be explained by the Eq. (3), which states that the Darcy velocity is directly proportional to the permeability if the pressure difference is constant.

Figure 2 Variation of the maximum value of the vertical component of Darcy's velocity with respect to the permeability from $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{16}}$ to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{13}}$ m². Red marks represent the permeability values where convection develops, while for blue marks values no convection is observed. Both axes are in logarithmic scale. In the convective regime (red dots), the behavior is fitted by a linear relationship: $v_{\mathrm{D}}=m\cdot k+b$, where m is 1.61×10⁷ and b is $-\mathrm{8.33}\times {\mathrm{10}}^{-\mathrm{9}}$.

3.2 3D benchmark results

The geometry of the model for the 3D benchmark, proposed in Magri et al. (2017), is composed by a 40 m wide, 5.5 km long fault, surrounded by a rock matrix ($\mathrm{5.5}\times \mathrm{5.5}\times \mathrm{5.5}$) km. The vertical fault is located in the center of the model, parallel to the y axis. In Fig. 3 we show the geometry of the model. Cubic meshes are used, the meshing within the fault is finer. The cubes are 40.14 m on each side in the enclosing rock, and in the fault they are 10.03 m on each side.

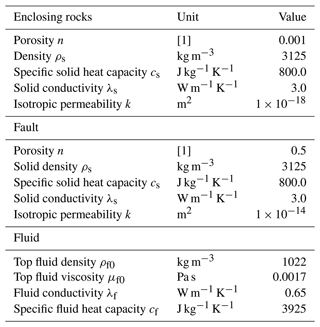
In consideration of the boundary conditions, the system is heated with a constant temperature of T_b=170 °C at the bottom of the model, while a constant temperature of T_c=20 °C is imposed at the top of the model. It is assumed that no thermal flow occurs on the remaining sides of the model. A pressure of 1×10⁵ Pa is imposed at the top of the model, with no flow on the other sides. These boundary conditions are expressed in Table 3. We report the properties of the enclosing rock, fault, and fluid in Table 4.

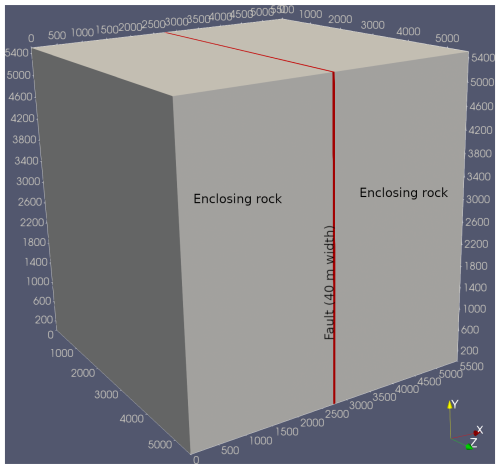
Figure 3 Faulted model used for the 3D benchmark according to Magri et al. (2017). The model has 5.5 km in the x, y, z directions, and contains a vertical fault with 40 m wide, and 5.5 km long, located at the center of the model, parallel to the y axis. The hexahedrons are 40.14 m on each side in the enclosing rock, and 10.03 m on each side within the fault.

Table 3 Boundary conditions used in Magri et al. (2017) for the 3D results.

Table 4 Values of the physical parameters used for the 3D benchmark according to Magri et al. (2017). Porosity values are on a scale from 0 to 1. Permeabilities are isotropic.

The fluid density ρ_f and viscosity μ_f follow the next laws:

$$\begin{array}{l}{\displaystyle }{\mathit{\rho }}_{\mathrm{f}}\left(T\right)={\mathit{\rho }}_{\mathrm{f}\mathrm{0}}\cdot (\mathrm{1}-\mathit{\beta }(T-T_{\mathrm{t}}\left)\right)\\ \text{(8)}& {\displaystyle }{\mathit{\mu }}_{\mathrm{f}}\left(T\right)={\mathit{\mu }}_{\mathrm{f}\mathrm{0}}\cdot \exp -{\displaystyle \frac{T-T_{\mathrm{t}}}{T_{\mathrm{v}}}},\end{array}$$

where ρ_f0=1022 kg m⁻³ and ${\mathit{\mu }}_{\mathrm{f}\mathrm{0}}=\mathrm{1.17}\times {\mathrm{10}}^{-\mathrm{3}}$ Pa s are the density and viscosity values at the top of the model, $\mathit{\beta }=\mathrm{5.9}\times {\mathrm{10}}^{-\mathrm{4}}$ °C⁻¹ is the fluid thermal expansion, T_t is the temperature at the top (20 °C), and T_v=62.1 °C, is an approximate temperature to fit fluid viscosity in Eq. (8) (see Wang et al., 1987, and Magri et al., 2017). The initial condition for temperature consists in a linear gradient from a temperature of 170 °C at the bottom to 20 °C at the top, therefore the gradient is approximately 27 °C km⁻¹. Additionally, a sinusoidal disturbance ϵ is added within the fault to trigger convection, and to have the same initial conditions proposed by Magri et al. (2017), as follows:

$$\begin{array}{}\text{(9)}& \mathit{ϵ}(x,y,z,t=\mathrm{0})=\sin \left(\mathit{\pi }z\right)\cos \left(\mathit{\pi }y\right)\end{array}$$

For the benchmark results, we follow Magri et al. (2017), but also Guillou-Frottier et al. (2020), where the 2017 3D benchmark was also reproduced. In the Fig. 4, we present a comparison between the thermal perturbation ($T-T(t=\mathrm{0}))$ within the fault at the time of 4027.14 kyr obtained in this work, and the results obtained in Magri et al. (2017). For this result we use an isotropic permeability of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{14}}$ m² in the fault. This value differs from the permeability originally reported ($\mathrm{1.019}\times {\mathrm{10}}^{-\mathrm{13}}$ m²) in Magri et al. (2017), but this value was not correct (Fabien Magri, personal communication, 2019). This permeability value (1$\times {\mathrm{10}}^{-\mathrm{14}}$ m²) was the best to reproduce the convective pattern and the thermal perturbation ($T-T(t=\mathrm{0}))$, which is in the range (−21 to 30) °C in our work, and (−20.62 to 28.94) °C in Magri et al. (2017).

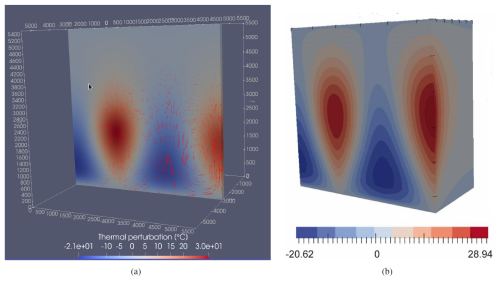
Figure 4 Comparison between the thermal perturbation in our benchmark result (a) and the results from Magri et al. (2017) (b), at a time of t=317.097 kyr. Thermal perturbation is defined as: T−T₀, where T₀ is the temperature at time t=0. The location of this result is in the fault (the red body defined in Fig. 3).

Table 5 Values taken from Magnenet et al. (2014) et Vallier et al. (2019) based on the Soultz-sous-Forets reservoir. The granite has a higher permeability value than sediments, because it represents an altered granite. This value was obtained after an inversion developed at Vallier et al. (2019), permeability here is isotropic. Porosity values are on a scale from 0 to 1.

4 Vendenheim site modeling

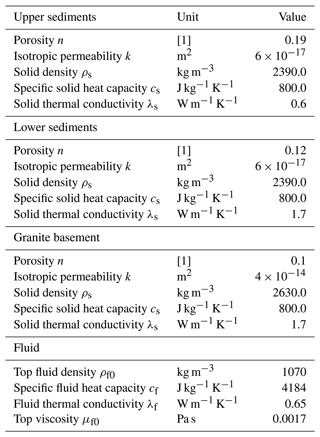
Figure 5 presents a simplified model of the Vendenheim site, which describes the main geological units in tabular form as a proxy for the sedimentary basin. These units include the granite basement, lower and upper sediments, which are located at depths deduced from the GEORG platform (Fig. 5). Each unit is homogenized and described by physical rock properties known at Soultz-sous-Forêts. Individual faults are not described as we search for large-scale hydro-thermal behavior. Previous studies (Vallier et al., 2019) have shown that regional faults have little impact on the local hydro-thermal behavior. The physical properties are taken from Vallier et al. (2019) (the name of the layers correspond to this article) and Magnenet et al. (2014), they are reported in Table 5. This properties are based on the units of the Soultz-sous-Forêts reservoir. The dimensions of the model are 6, 8, and 8 km in the x, y, and z directions respectively, with 100 m per side hexahedral elements. The upper boundary represents the Earth's surface.

The physical laws governing fluid density ρ_f and viscosity μ are identical to those presented in Magri et al. (2017) (Eq. 8). In this study we use the reported values of ρ_f0 and μ_f0, as presented in Table 5, to develop our analytical framework.

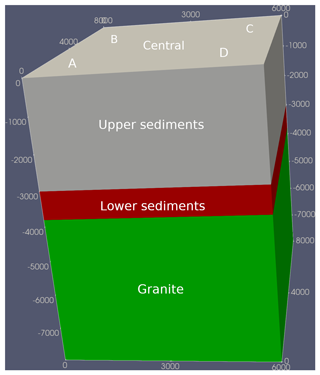
Figure 5 Simplified model based in the GEORG platform (https://maps.geopotenziale.eu, last access: 8 October 2024) over the Vendenheim site (North Strasbourg, France) and in the 2D model proposed in Vallier et al. (2019). The coordinates of the A, B, C, D, and central points, that refer to the location of the profiles of Fig. 6, are in kilometers respectively: (1.5,2), (4.5,2), (4.5,6), (1.5,6), (3,4).

Numerical solution

The boundary conditions exhibit no mass flow at all boundaries, except for the top boundary where the atmospheric pressure value is imposed. For temperature, heat flow is zero at all boundaries except for the top boundary where a value of 15 °C, that represents the average air temperature at the surface, is imposed. And at the bottom boundary, the system is heated with a value of 423 °C. This boundary conditions are presented in Table 6.

Table 6 Boundary conditions used for the 3D results in the homogeneous model of Strasbourg.

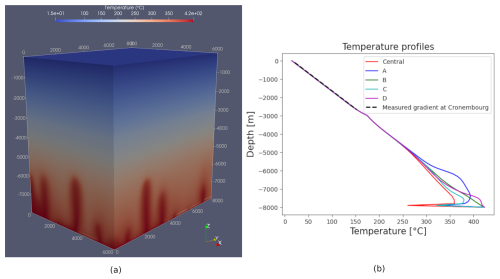
Figure 6 (a) Temperature distribution in 4.77 kyr, with a convective regime in the granite and a conductive regime in the sediments. The horizontal width of the convection cells measure between 780 and 880 m. (b) Profiles showing the temperature along vertical lines at the different points A, B, C, D, Central, introduced in Fig. 5. We show the measured temperature profile at Cronembourg area. The Rayleigh number for the granite lower and upper sediments are 536, 0.0280, and 1.07 respectively.

The distribution map of temperature and profiles using the properties of Table 5 are shown in Fig. 6 at the time of 4.77 kyr. We choose a time when the convective patterns have already formed. We observe a transient convective regime in the granite and a conductive regime in the sediments. The Rayleigh number in the granite, upper and lower sediments are 536 and 1.07, and 0.0289 respectively, the critical Rayleigh number being 4π²=39.47. Therefore, convection is expected in the granite but not in the sediments. In the vertical temperature profiles we added the measured temperature profile at Cronembourg site (at a distance of aproximately 9 km from the Vendenheim site), measured by the “Bureau de Recherches Geologiques et Minieres” (BRGM) (personal communication, 1982), which is 5.10 °C per 100 m, showing that there exist a good fit between the calculated profiles and this gradient. The profiles show that the transition between the conductive and convective regimes occurs at a depth of about 5 km, according to Schmittbuhl et al. (2021) the earthquakes in the site are globally at a depth of about 5 km. This means that there may be a relationship between the transition region between the conductive and convective regimes and the region of the area where the induced earthquakes were generated.

5 Conclusions

We solve 2D and 3D benchmarks to test our methods based in TH coupled system, using the moose-based open-source application “Golem”. We show that for the 2D benchmark where the thickness is 1500 m, a transition from conductive to free convective solution exist for a permeability of the order of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{16}}$ m² with a Darcy velocity at a maximum of the order of several decimeters per year.

We developed a simplified model of the Vendenheim site, based on the regional geological model Georg, we apply a TH coupled system in this model, using the rock and fluid physical properties from previous studies at Soultz-sous-Foréts but adjusting their depths according to the features of the local geological model. We conclude that given the observed parameters at the Vendenheim site, a transient hydrothermal convective regime is observed at the granite, while a conductive behaviour is observed in the sediments. The approximate depth of induced seismic events (5 km) in the region coincides with the depth of the transition between the convective and conductive zones. However, as stated in the Introduction, exploring this possible relationship is beyond the scope of this article. Therefore, this work serves to establish the initial conditions for a future induced-seismicity model in the Vendenheim area.