Hysteresis in permeability evolution simulated for a sandstone by mineral precipitation and dissolution

Mineral dissolution and precipitation can substantially affect rock permeability, which is a critical parameter for a broad range of geological subsurface applications. Virtual experiments on digital pore-scale samples represent a powerful and flexible approach to understand the impact of microstructural alterations on evolving hydraulic rock behaviour and quantify trends in permeability.

In the present study, porosity-permeability relations are simulated for a precipitation-dissolution cycle within a typical reservoir sandstone. A hysteresis in permeability is observed depending on the geochemical process and dominating reaction regime, whereby permeability of the six investigated reaction paths varies by more than two orders of magnitude at a porosity of 17 %. Controlling parameters for this hysteresis phenomenon are the closure and re-opening of micro-scale flow channels, derived from changes in pore throat diameter and connectivity of the pore network. In general, a transport-limited regime exhibits a stronger impact on permeability than a reaction-limited regime, which uniformly alters the pore space. In case of mineral precipitation, higher permeability reduction results from successive clogging of pore throats, whereas in case of dissolution, permeability significantly increases due to a widening of existing flow paths. Both, the geochemical process and dominating reaction regime govern characteristic microstructural alterations, which cannot be simply reversed by the inversion of the geochemical processes itself. Hence, permeability evolution clearly depends on the hydrogeochemical history of the sample.

1 Introduction

Permeability is a crucial hydrogeological parameter for the characterisation of fluid flow in porous media and highly relevant for a broad range of geological subsurface applications, including geothermal energy recovery, carbon dioxide, natural gas and hydrogen storage or hydrocarbon production, as well as subsurface contaminant transport (De Lucia et al., 2011; Jacquey et al., 2015; Hofmann et al., 2014; Kleinitz et al., 2001; Regenspurg et al., 2015). Analytical or empirical methods are commonly applied in reservoir models to estimate evolving permeability trends. These approaches generally describe permeability as a function of porosity (Bernabé et al., 2003; Ma, 2015), such as the Kozeny-Carman relationship (Carman, 1937) or the power law (Hommel et al., 2018). However, their predictive capabilities are limited, since they have been originally developed for idealised microstructures. In general, mineral precipitation reduces the porosity of a rock (Fig. 1), but its effect on transport properties strongly depends on the specific spatial alterations of the microstructure. Thus, porosity-permeability relationships can be more complex especially for geochemical processes, because mineral precipitation and/or dissolution locally change the pore structure, and thus the flow field, e.g. by closing or opening preferential flow paths. The resulting non-uniform permeability response cannot be captured by common analytical approaches (Beckingham, 2017; Lesueur et al., 2020).

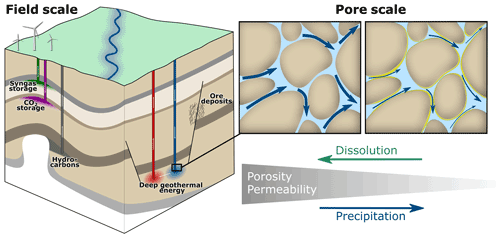
Figure 1 The geological subsurface is of essential relevance for a broad range of applications. Geochemical processes alter the microstructure of rocks, which in turn affects their hydraulic behaviour on the macro scale, and thereby governs the evolution of geological subsurface systems.

Numerical simulations on pore-scale samples represent a flexible method to determine fundamental rock property relations (Berg et al., 2017). In this context, the research field of digital rock physics comprises the numerical simulation of hydraulic (Blunt et al., 2013; Herring et al., 2017), elastic (Andrä et al., 2013; Shulakova et al., 2017), electric (Keehm et al., 2001; Wu et al., 2020) and/or thermal properties (Ettemeyer et al., 2020; Schepp et al., 2020), which are directly calculated on digital samples, mainly derived from micro-CT scans. These virtual experiments offer a non-destructive method with direct access to rock parameters, which is further applied to compute evolving trends in rock properties based on microstructural changes (Niu and Zhang, 2019; Noiriel et al., 2016; Sain et al., 2016; Wetzel et al., 2020b).

Within the presented study, a cycle of secondary mineral precipitation and subsequent dissolution is simulated for a synthetic sample of a Fontainebleau sandstone. Trends in permeability are computed for two contrasting geochemical reaction regimes: (1) a transport-limited and (2) a surface reaction-limited regime. Moreover, morphometric parameters of the pore space are computed and analysed to quantify arising changes in the microstructure and understand hydraulic impacts depending on the prevailing geochemical processes and reaction regimes.

Figure 2 (a) Virtual sample of the unaltered synthetic sandstone including the flow field, represented by streamlines coloured by the local fluid flow velocity. Frequency distribution of the (b) pore throat size and (c) connectivity of the pore network with their respective average value.

2 Materials and methods

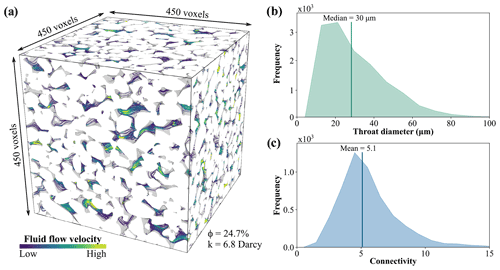
In the present study, a digital sample of a highly porous sandstone is synthetically generated to allow for an assessment of the reaction-induced permeability evolution over a preferably wide range of porosities. Therefore, a process-based approach is applied, combining the gravity-driven deposition of irregularly shaped grains, and their diagenetic cementation. A more detailed description of this concept is provided in Wetzel et al. (2021), demonstrating that the constructed homogenous sandstone samples show microstructural and physical properties comparable to their natural equivalents. Grain size distribution and grain shape of a Fontainebleau sandstone are applied to generate the synthetic sample, since it represents a comprehensively examined reference rock for reservoir engineering applications (Gomez et al., 2010; Walderhaug et al., 2012). The virtual sandstone investigated here has a resolution of 450³ voxels with an edge length of 5 µm, whereby the total porosity of the unaltered sample is 24.7 % (Fig. 2a).

The morphometric parameters of the pore space are calculated using the Python package PoreSpy (Gostick et al., 2019). In order to quantify changes within the pore space, the individual pores are initially extracted for the unaltered microstructure by means of a watershed segmentation. Then, labelling of the pores is maintained and overlaid by the altered microstructure, so that variations in pore morphology due to the simulated alterations can be calculated. Thus, median pore throat diameter and mean connectivity of the pore network are determined, whereby the latter represents the number of throats connected to a single pore (Fig. 2b and c).

Permeability is calculated from the flow field by solving the steady-state Stokes equation using the OpenFOAM software package (Weller et al., 1998). The virtual experiment simulates a cycle of (1) precipitation of an arbitrary secondary mineral until the sample is nearly impermeable, and (2) the subsequent dissolution of the previously precipitated mineral. Corresponding trends in permeability are further determined for two contrasting geochemical reaction regimes, presupposing that the system is generally advection‐dominated (high Péclet numbers). In case of a surface reaction-limited process, the chemical reaction rate is the limiting factor, and the pore space is altered uniformly around the grains (Damköhler number ≪1). For the transport-limited alteration, the chemical reaction is limited by the availability of reactants, which are transported to the fluid-rock interface (Damköhler number ≫1). In this case, the local velocity is used as a proxy for solvent flux, and precipitation as well as dissolution are defined to occur in regions of high flow velocities (>75th percentile). A detailed description of this iterative approach can be found in Wetzel et al. (2020a). The aim of this simplification is to approximate characteristic precipitation and dissolution patterns instead of performing fully-coupled reactive transport simulations. Thus, a bandwidth of hydraulic property changes can be investigated for, e.g., sandstones or carbonates (Niu and Zhang, 2019; Miller et al., 2017), whereby the simulated porosity-permeability curves are comparable to experimentally determined relations (Wetzel, 2021).

3 Results

3.1 Precipitation paths

The precipitation of an arbitrary secondary mineral by the two contrasting geochemical reaction regimes leads to distinctive alteration patterns of the pore space. The surface reaction-limited precipitation uniformly alters the pore structure. All pores are equally affected, which illustrates the continuous reduction in pore throat diameter and connectivity of the pore network. At a porosity of 6 %, the virtual sample becomes nearly impermeable and precipitation is stopped. The resulting decrease in permeability for the reaction-limited regime can be approximated by the power law with an exponent of four (Fig. 3a).

By contrast, the transport-limited regime shows by definition a localised precipitation in areas of high fluid flow velocities. This leads to a preferential clogging of pore throats, indicated by the morphometric evolution of the pore space (Fig. 3b): (I) First, fluid flow paths become narrower, since the median pore throat diameter is strongly reduced, while simultaneously the connectivity of the pore network is changed only slightly. (II) Successive mineral growth leads to a closure of fluid flow paths, whereby connectivity of the pore network is drastically reduced, while the throat diameter is less affected. The described morphological alteration of the pore space is the reason for the steep permeability decrease, whereby the porosity-permeability relation can be described by the power law with an exponent above ten. Consequently, low permeabilities comparable to the reaction-limited alteration are reached at a considerably higher porosity of 15 %, and the amount of precipitated minerals is significantly lower.

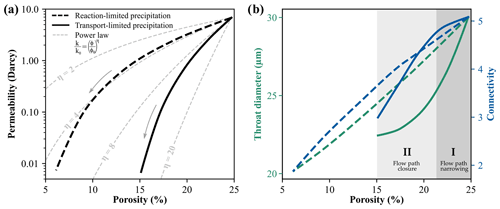
Figure 3 (a) Simulated porosity-permeability trends for reaction- and transport-limited precipitation regimes compared to analytical relations based on the power law with different exponents (η). (b) Evolution of median throat diameter and mean connectivity for both chemical regimes with the characteristic phases of (I) flow path narrowing and subsequent their complete clogging (II).

3.2 Dissolution paths

The subsequent mineral dissolution also shows characteristic morphometric alterations of the pore space, depending on the dominant geochemical reaction regime. The initial microstructure and permeability (Fig. 4a) will be achieved by definition, since the quartz grains are considered as inert and only the previously precipitated minerals can be dissolved. In case of reaction-limited dissolution, (I) the pore structure is initially uniformly affected, so that the pore throat diameter and connectivity of the pore network constantly decrease (Fig. 4c). Since the fluid-mineral contact area is substantially lower in narrow throats, which are filled with the previously precipitated minerals, it takes additional iterations for their uniform dissolution. Hence, a substantial amount of 53 % of the pore throats is still filled with secondary minerals at the high porosities of 19 % (Fig. 4d). Thus, (II) dissolution of these narrow throats leads to a drastic increase in connectivity of the pore network, and simultaneously reduces the median throat diameter. Nevertheless, the permeability curve of the sample is still continuous and does not exhibit any sharp changes. The porosity-permeability relation of the reaction-limited dissolution regime can be approximated by the power law with an exponent of five.

The transport-limited mineral dissolution (I) initially exhibits a widening of the existing main flow paths, indicated by a sharp increase in the throat diameter, while the pore network connectivity remains nearly constant (Fig. 4c). Fluid flow velocities substantially increase in these flow paths, since flow is channelled and all of the previously precipitated minerals in the respective pores are dissolved (Fig. 4d). (II) Successive mineral dissolution leads to the development of new flow paths, where connectivity of the pore network constantly increases and throat diameters slightly widen. (III) As for the reaction-limited regime, secondary minerals in narrow throats exhibiting a lower fluid-to-mineral interface are dissolved, what demonstrates the decrease in the median throat diameter resulting from the increasing amount of newly dissolved small throats. The previously described steps of the morphological alteration result in a non-uniform porosity-permeability relation, comprising a steep initial increase due to the fluid flow path widening, followed by a comparably lower permeability increase until the initial state is reached again (Fig. 4a).

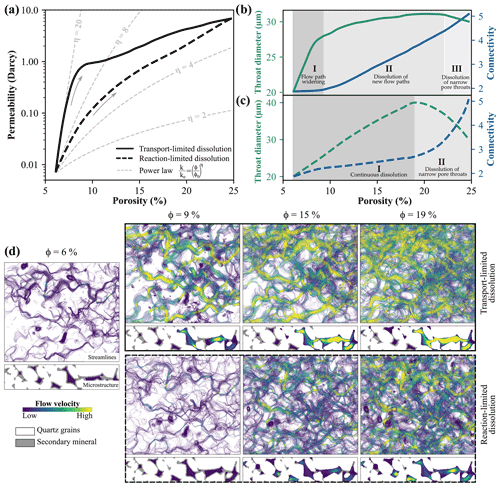
Figure 4 (a) Simulated porosity-permeability trends for reaction- and transport-limited dissolution compared to analytical power law relations with different exponents (η). Evolution of median throat diameter and mean connectivity for the (b) transport- and (c) reaction-limited regimes with phases of characteristic morphometric evolution. (d) Differences in the flow field between both dissolution regimes represented by streamlines (x–y projection of the 3D sample) as well as the microstructure (2D slice).

3.3 Permeability hysteresis of the precipitation-dissolution cycle

The precipitation-dissolution cycle under the assumption of two contrasting geochemical reaction regimes was investigated by means of six simulation scenarios with different porosity-permeability relationships (Fig. 5a). A hysteresis in the evolution of hydraulic properties depending on the geochemical process and dominating reaction regime can be observed. Controlling parameters for this phenomenon are characteristic changes of the pore space, as the closing or opening of flow channels described in Sect. 3.1 and 3.2.

Reaction-limited precipitation (Scenario 1) and subsequent dissolution (Scenario 1b) uniformly alter the pore structure, and thus largely show continuous changes in pore throat diameters and connectivity (Fig. 5b). Thus, permeability is constantly changed in both cases. Permeabilities of the dissolution path (Scenario 1b) are consistently lower due to the smaller fluid-to-mineral interface of the narrow throats, filled with the previously precipitated minerals. Also for Scenario 2b, the reaction-limited dissolution mostly leads to uniform changes in throat diameters and pore network connectivity (Fig. 5b). Nevertheless, the parameter evolution depends on the initial distribution of secondary minerals. Since previous precipitation preferentially occurs in pore throats (Fig. 6b), uniform dissolution leads to a comparatively gentle increase in the hydraulic properties, exhibiting the lowest permeabilities of all investigated scenarios (Fig. 5a).

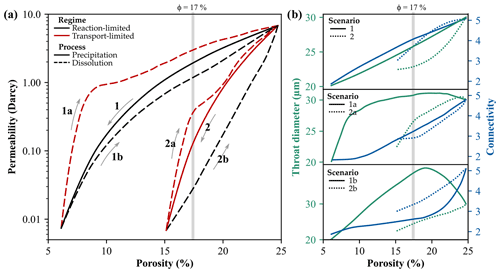
Figure 5 (a) Porosity-permeability curves for the six investigated reaction paths of the simulated precipitation-dissolution cycle. (b) Characteristic evolution of the median throat diameter (green) and mean connectivity (blue) depend on the geochemical process and dominating reaction regime. At a porosity of 17 %, permeability varies by more than two orders of magnitude.

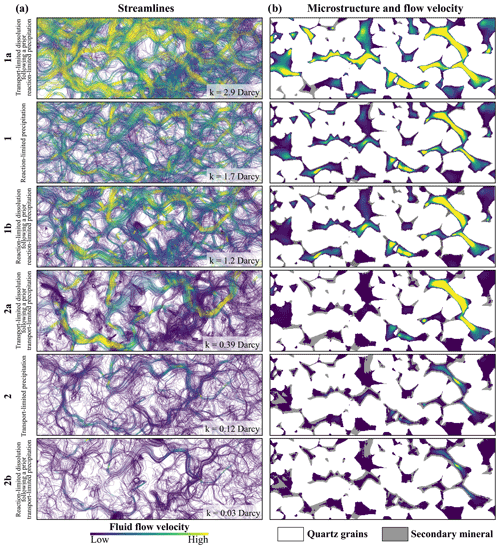
Figure 6 (a) Characteristic differences in the fluid flow regime represented by streamlines (x–y projection of the 3D sample) at a porosity of 17.4 %, where permeability varies by more than two orders in magnitude. (b) Comparison of characteristic morphometric differences and the local flow velocities within the pore space for the six simulation scenarios (1a–2b).

Transport-limited geochemical processes exhibit characteristic non-uniform alteration patterns, where flow paths are systematically clogged or dissolved. The narrowing of pore throats and their successive closure are typical for the precipitation processes occurring in this reaction regime (Scenario 2) and result in a comparably steep permeability decrease (Fig. 5a). The transport-limited dissolution of minerals (Scenarios 1a and 2a) in turn initially lead to a predominant widening of existing fluid flow paths and force channelised flow. This exhibits the sharp increase in the throat diameter, while connectivity remains nearly constant, resulting in a steep porosity-permeability curve (Fig. 5b). Successive mineral dissolution then induces new fluid flow paths, what increases the pore network connectivity and leads to a less pronounced increase in permeability. In general, this characteristic evolution can be observed for both transport-limited dissolution scenarios, but the intensity of each phase depends on the spatial distribution pattern of the previously precipitated minerals. In Scenario 2a, these dissolution steps are less prominent, since secondary minerals are initially localised around pore throats, what reduces the effect of flow path widening and the related intensity of the permeability increase (Fig. 5a and b).

Thus, a permeability hysteresis depending on the geochemical process and dominating reaction regime can be observed. In general, reaction-limited precipitation results in higher permeabilities than transport-limited precipitation. Analogously, transport-limited dissolution processes exhibit consistently higher permeabilities than the respective precipitation path and the reaction-limited dissolution (Fig. 5a). For the same porosity of 17 %, permeability varies by more than two orders in magnitude between the six simulated scenarios. Reaction-limited precipitation followed by a transport-limited dissolution (Scenario 1a) exhibits the highest permeability of 2.9 Darcy (1 Darcy = $\mathrm{9.869}\times {\mathrm{10}}^{-\mathrm{13}}$ m²) due to the initially uniform precipitation and fluid flow channelling, resulting from preferential mineral dissolution inside the main fluid flow paths (Fig. 6a and b). Lowest permeabilities of 30 Millidarcy occur in Scenario 2b, since the previous transport-limited precipitation preferentially clogged pore throats, while the uniform reaction-limited dissolution requires more iterations to extend narrow throats due to the smaller fluid-to-mineral interface (Fig. 6b). Hence, the results clearly illustrate that permeability evolution depends on the geochemical history of a rock sample, where both the geochemical process and dominating reaction regime govern characteristic microstructural alterations within the pore space. These cannot be simply reversed by the inversion of the geochemical processes itself, so that the respective paths require specific assessments.

4 Discussion

The observed permeability hysteresis of the investigated geochemical cycle of secondary mineral precipitation and its subsequent dissolution can be explained by characteristic morphometric alterations of the pore space. Controlling parameters for the observed changes in hydraulic parameters are the clogging and re-opening of pore-scale fluid flow channels, which can be quantified by the pore throat diameter and connectivity of the pore network. The observed predominant clogging of pore throats as well as the related drastic permeability decrease in the transport-limited precipitation regime have been reported by several studies (Tenthorey and Scholz, 2002; Crandell et al., 2012; Niu and Zhang, 2019). Also the selective widening of fluid flow paths and a flow channelling by preferential pathways are well aligned with observations from experiments, especially for evolving wormholes in carbonatic rocks (Lebedev et al., 2017; Luquot et al., 2016; Menke et al., 2014; Miller et al., 2017), and have been also observed for strongly cemented sandstones (Kühn, 2004).

Lesueur et al. (2020) modelled a dissolution-precipitation cycle by uniformly altering digital rock samples and reported a persisting permeability increase. For a sandstone sample, they demonstrated the presence of a hysteresis phenomenon, where the final permeability is less than 3 % above the initial one. In contrast, a permeability increase of 110 % has been observed for a carbonate sample. In the models presented in this study, the initial permeability is achieved by definition, since only the previously precipitated minerals can be dissolved, while the granular structure is considered as inert. Nevertheless, there is a clear tendency showing that reaction-limited dissolution leads to lower permeabilities compared to the previous precipitation path, since dissolution cannot restore all pore thoats previously filled by mineral precipitation. This is in agreement with the work of Lesueur et al. (2020), where for the reverse cycle of dissolution followed by precipitation permeabilities increase, since dissolved new fluid flow channels remained open after mineral precipitation. Hence, considering a reaction-limited regime, a dissolution-precipitation cycle would result in consistently higher permeabilities compared to the initial state, whereas a precipitation-dissolution cycle would induce a decrease in permeability. Moreover, even if not investigated here, the hysteresis phenomenon and associated permeability changes will be more pronounced in carbonates or rocks in which the entire microstructure can be chemically altered. For example, the bend within the porosity-permeability curve due to the change from flow path widening to the development of new flow paths is associated with the underlying microstructure of the transport-limited dissolution Scenarios 1a and 2a. Since only secondary minerals within an inert granular structure are allowed to be dissolved, the remaining flow paths will be dissolved by definition. In contrast to this, flow path widening and flow channelling would continue in carbonates.

Nevertheless, the investigated geochemical reaction regimes are end-members and reactive transport is more complex and not exclusively depending on fluid flow velocity. Chemical reactions are controlled by various other factors like fluid chemistry, mineralogy, temperature, pore morphology, pore and lithological pressures as well as transport properties (Cil et al., 2017; Fazeli et al., 2020; Schepers and Milsch, 2013; Beckingham, 2017). Moreover, the presented approach presumes advection-dominated species transport and implicitly neglects diffusion. This is considered as a valid assumption for many applications in geological subsurface systems. Despite the fact that the field of physical pore-scale simulations is quickly evolving due to increasing computational efficiency, there are up to now no studies known which explicitly perform reactive transport simulations for mineral precipitation and dissolution on realistic three-dimensional pore space models at the given spatial discretisation. In this regard, the presented approach and investigated scenarios represent a flexible and moreover feasible method to quantify permeability trends and support the understanding of the hydraulic impact of microstructural alterations.

5 Conclusions

In this study, porosity-permeability trends are computed for a precipitation-dissolution cycle within a typical reservoir sandstone. Virtual experiments are performed, simulating secondary mineral precipitation within the pore space until the sample is nearly impermeable, and the subsequent dissolution of the previously precipitated minerals. Two contrasting geochemical reaction regimes are assessed, which govern the preferential location of the alteration in the pore space.

The resulting six scenarios of the investigated precipitation-dissolution cycle clearly show a permeability hysteresis, depending on the geochemical process and dominating reaction regime. Hereby, permeability varies by more than two orders of magnitude for the same porosity of 17 %. Controlling parameters for this hysteresis phenomenon are the closure and re-opening of pore-scale fluid flow channels, which can be quantified by the morphometric parameters pore throat diameter and connectivity of the pore network. In general, a transport-limited regime exhibits a stronger impact on permeability compared to the reaction-limited geochemical regime, which uniformly alters the pore space. Transport-limited precipitation is characterised by the narrowing of pore throats and their successive closure, resulting in a comparably high permeability reduction. Transport-limited dissolution in turn leads to a predominant widening of existing flow paths, and thereby a significant increase in permeability. Reaction-limited processes uniformly alter the pore structure, whereby permeability is continuously changed. Nevertheless, permeabilities of the reaction-limited dissolution paths are consistently lower compared to the precipitation paths, due to a smaller fluid-to-mineral interface of the narrow throats filled with the previously precipitated minerals.

The results clearly illustrate that the permeability evolution is history-dependent, where both the geochemical process and the dominating reaction regime govern the characteristic microstructural alterations of the pore space, which cannot be simply reversed by an inversion of the geochemical processes itself. The presented modelling approach enables to simulate cycles of precipitation and dissolution on highly resolved three-dimensional pore space models without the requirement of implementing complex and computationally expensive reactive transport simulations. Both evolving trends in permeability and causal changes in pore morphology can be quantified, and thereby explain the impact of microstructural alterations on hydraulic rock properties. Hence, the proposed method is of essential importance for a wide range of natural and engineered subsurface applications, since it improves process understanding, and thereby the predictive capabilities of reservoir models.