An analysis of a priori and empirical solar radiation pressure models for GPS satellites
Xiao Chang
Benjamin Männel
Harald Schuh
Among the different non-conservative forces acting on GPS satellites, solar radiation pressure (SRP) has the greatest influence and inappropriate modeling of it can introduce an acceleration with the order of 1 × 10−7 m s−2. There are a variety of empirical, analytical, and hybrid empirical-physical models to describe the SRP effect. Among them, the empirical model developed at the Center for Orbit Determination in Europe (CODE) and analytical models based on a box-wing prototype, namely box-shape bus with solar panels, are widely used in the International GNSS Service (IGS) community. To investigate the effects of different a priori SRP models on top of empirical parameterization, two sets of parameters based on the Empirical CODE Orbit Model (ECOM) and two a priori models including the analytical box-wing model and the empirical GPS Solar Pressure Model (GSPM) are tested for the different GPS satellites. Orbit comparison of different SRP scenarios shows that: (1) the two parameterizations of ECOM perform differently for Block IIA and IIR/IIR-M satellites but lead to fewer differences for Block IIF satellites in terms of orbit difference pattern. The 3D RMS of orbit difference of two parameterizations are 25, 30 and 21 mm for each block type. (2) Adoption of a priori model or change of the ECOM parameterization mainly lead to orbit differences varying with both elevation of the Sun w.r.t. the orbit plane and the satellites' argument of latitude w.r.t. the noon point, which is supposed to be related to the special geometry and attitude of every block type. These differences are especially obvious in radial direction. Analysis of estimated parameters of ECOM indicates that (3) the GSPM.04 performs better than box-wing model to describe the main constant solar radiation. It is found (4) that the asymmetry of estimated ECOM parameters in B direction (i.e., the direction completing the orthogonal system with D direction and satellite's solar panel axes), observed for three Block IIR satellites, causes corresponding asymmetrical orbit differences in radial direction when reduced ECOM parameters are used. This does not apply to the extended ECOM parameterization tested in this study, which indicates the insufficiency of reduced ECOM to parameterize asymmetrical satellites.
- Article
(6252 KB) - Full-text XML
- BibTeX
- EndNote
Beginning with the first generation, namely the Block I, GPS has experienced a development of over forty years to its third generation and operates currently 31 satellites of Block IIR/IIR-M, Block IIF and Block III as of 5 June 20201. The GPS satellites differ not only between generations (namely termed with I, II and III), but also within the same generation with different block types in terms of spacecraft geometry (Montenbruck et al., 2015), which lead to significant differences in the acceleration caused by solar radiation pressure (SRP). Accompanying by the development of GPS, methods to describe the SRP effect on GPS satellites have been proposed and the developed models could be generally categorized as (1) analytical model, (2) empirical model, and combination of both, (3) the hybrid empirical-physical model. Fliegel et al. (1992); Fliegel and Gallini (1996) improved the ROCK models to describe the solar radiation force acting on the body-fixed X and Z surface for Block I, II/IIA and IIR satellites with T-series model. Based on the dimension and optical properties, the force are formed of a Fourier series with the Earth-satellite-Sun angle as the angular argument. Besides, it is advised to estimate a scaling factor of the force and the so-called Y-bias. Concerning that one scale factor might not be enough to absorb the error introduced by the a priori model, Beutler et al. (1994) presented an empirical model called the Empirical CODE Orbit Model (ECOM). In the ECOM model, the acceleration is decomposed in three orthogonal directions and given in the form of a Fourier series expansion in each. The argument of latitude of the satellite is taken as the angular argument. The original ECOM was later optimized by Springer et al. (1999) to the one called reduced ECOM (ECOM-1) and then further developed by Arnold et al. (2015) to the new extended ECOM (ECOM-2) to fix the model shortcoming when used for GLONASS. The SRP models used in the Jet Propulsion Laboratory (JPL) also originate from what Fliegel et al. (1992) and Fliegel and Gallini (1996)) have proposed but were improved to what is called GPS Solar Pressure Model (GSPM) model (Bar-Sever and Russ, 1997; Bar-Sever and Kuang, 2004; Sibthorpe et al., 2010; Sibois et al., 2014; Sakumura et al., 2017). Similar to ECOM models, the GSPM models decompose the acceleration into three orthogonal but different components based on body-fixed frame except for the initial GSPM.97 (Bar-Sever and Russ, 1997) and the Earth-satellite-Sun angle is taken as the expansion variable. The coefficients of GSPM are fixed based on long-term observation fit and extra parameters, like the scaling factor in body-fixed X and Z directions and the y-axis bias, are estimated. In consideration of the advantages and disadvantages of both analytical and empirical SRP models, Rodríguez-Solano et al. (2012) derived the adjustable box-wing model based on the physical interaction between the direct solar radiation and satellite surfaces and meanwhile considering other unmodeled errors like the solar panel rotation lag. While there are lots of candidate models that could be used for modeling the SRP, it is hard to tell which model or which combination of models is the most suitable. Assessing the models' performance when they are used independently and combined would show the pros and cons of each model and thus help to optimize the SRP modeling strategy. In this study, the widely used ECOM parameterization and two a priori SRP models, the box-wing model (Rodríguez-Solano et al., 2012) and GSPM.04 a priori model (Bar-Sever and Kuang, 2004) are analyzed in terms of the orbit quality and the estimated ECOM parameters. This paper is organized as follows: the methodology, including the data, the processing strategies and analysis methods, are introduced in Sect. 2. Section 3 presents the orbit comparison results for the different GPS block types. The orbit comparison between IGS final orbits and those based on different SRP schemes shows the performance of a variety of combination strategies of a priori models and ECOM parameterizations. Furthermore, the comparison of different a priori information based on the same ECOM parameterization is conducted to evaluate the effect of a priori model on orbits. In Sect. 4, the characteristics of estimated ECOM parameters based on different combination of parameterizations and a priori SRP models are discussed. The conclusions and perspectives are summarized in Sect. 5.
The box-wing model and GSPM.04 a priori model in this article are implemented based on what Rodríguez-Solano et al. (2012) and Bar-Sever and Kuang (2004), respectively, have presented in previous research. More precisely, only the box-wing model based on provided optical properties and geometry information is used to describe the a priori acceleration without adjustments for the optical parameters nor the extra ones like the solar panel rotation lag. For GSPM.04 model, the coefficients of the a priori part are used but the other parameters are not taken into consideration. The scale factor for GSPM.04 is set as 1 to keep the consistency with the box-wing model. This assumption should be reasonable since the estimated scale factor just shows a few percent difference from 1 according to Bar-Sever and Russ (1997). It is worthwhile to note since the coefficients of the upgraded GSPM models are not presented in the relevant study (Sibthorpe et al., 2010; Sibois et al., 2014; Sakumura et al., 2017), the coefficients of GSPM.04 are used for our analysis. As for the empirical parameterization method, the ECOM models are used, which decompose the acceleration caused by SRP into the following three directions (Arnold et al., 2015):
where rs and r are the geocentric vectors of the Sun and the satellite, respectively. The vector er is the unit vector associated with r and eD is the unit vector from satellite to the Sun. The vector eY points along the solar panel axis and eB completes the right-handed system. Thus, the total acceleration due to SRP could be written as
in which a0 describes the acceleration based on an a priori model and the coefficients D, Y and B consist of constant and harmonic terms. For the extended ECOM, the coefficient of each component in Eq. (2) is given as truncated Fourier series in Eq. (3), with the angular argument replacing the satellite's argument of latitude u used in former ECOM model. The us is the Sun's argument of latitude in the satellite's orbital plane (Arnold et al., 2015).
In this study, two sets of nD and nB are used to evaluate the different ECOM parameterizations, namely the reduced ECOM () and the D4B1 scenario () suggested by Arnold et al. (2015). The ECOM parameterizations are taken as prerequisite part to absorb the unmodeled or mis-modeled error in this study and thus the a priori models are investigated on top of an ECOM parameterization. Furthermore, we could also assess the estimated ECOM parameters. Combining the different a priori model and ECOM parameterization, we have the following six scenarios:
-
ECOM1: the reduced ECOM parameterization, with three constant coefficients in D, Y and B and once-per-revolution (1pr) terms in B, without an a priori model.
-
ECOM2: the D4B1 parameterization, with twice-per-revolution (2pr) and fourth-per-revolution (4pr) terms in D and 1pr in B besides of constant coefficients in three components, without an a priori model.
-
GSPM1: ECOM1 with the GSPM.04 a priori model.
-
GSPM2: ECOM2 with the GSPM.04 a priori model.
-
BOXW1: ECOM1 with the box-wing model presented by Rodríguez-Solano et al. (2012).
-
BOXW2: ECOM2 with the box-wing model presented by Rodríguez-Solano et al. (2012).
The other models are common for all tested scenarios following the rapid product series strategy of GFZ2 (Männel et al., 2020). As for the specific attitudes of different block types, the modeling is based on nominal yaw-attitude (Bar-Sever, 1996). When satellites are in noon turn or mid-night turn, the model developed by Kouba (2009) is applied for Block IIA and Block IIR/IIR-M satellites and the attitude for Block IIF satellites is derived according to Dilssner (2010). Applying the SRP strategies and models' information mentioned above, the data spanning the whole year of 2018 (GPS weeks 1982-1 to 2034-1) are processed using EPOS.P8 software developed at GFZ. It should be noted that in total 32 satellites (1 Block IIA, 19 Block IIR/IIR-M and 12 Block IIF) were available during this period. The Pseudo-Random Noise (PRN) number G18 was assigned to the satellite with Space Vehicle Number (SVN) 054 till 23 January 2018 and later on transmitted by SVN 034 on 20 March 2018.
The perturbation difference introduced by different modeling of the solar radiation pressure could be reflected by the satellite orbit. In this section, the precise orbits produced with different scenarios are evaluated.
3.1 Comparison with IGS final orbits
For validation with external orbits, the final orbit products provided by the International GNSS service (IGS, Johnston et al., 2017) are used as reference. Table 1 gives the Root Mean Square (RMS) and average value of orbit differences between IGS and different scenarios in the three directions of orbit frame, i.e., along-track (T), cross-track (N) and radial (R) directions. As GSPM.04 provides coefficients of a priori model only for Block IIA and Block IIR satellites, the orbit comparison results of GSPM1 and GSPM2 for Block IIF are, therefore, not shown in the table and the coefficients used for Block IIR-M are the same as those for Block IIR (thus the name IIRg in following contents is used to represent the group of satellites for IIR and IIR-M). It could be seen from Table 1 that: firstly for all block types, the RMS of orbit differences between IGS and ECOM1, ECOM2, BOXW1 and BOXW2 are generally within 20 mm in each direction and the use of GSPM.04 based on ECOM parameterization would degrade the orbit consistency with IGS final orbit. Especially for IIR/IIR-M satellites, the RMS of orbit differences in radial direction could reach 44.5 and 35.8 mm for GSPM1 and GSPM2, respectively; secondly for Block IIA and IIF satellites, the orbit based on ECOM1 are the most consistent with IGS final orbit while for Block IIR/IIR-M the orbit based on ECOM2 shows the best consistency. The RMS of orbit differences between IGS and ECOM1 are 14.9, 11.7 and 10.9 mm for Block IIA and 12.2, 11.3 and 8.9 mm for Block IIF in along-track, cross-track and radial directions, respectively. For Block IIR/IIR-M, the RMS of orbit differences between IGS and ECOM2 are 12.0, 11.9 and 14.6 mm in above three directions.
Table 1The RMS and average value of orbit differences between operational IGS final products and different scenarios for Block IIA, IIR/IIR-M and IIF in along-track (T), cross-track (N) and radial (R) directions (unit: mm).
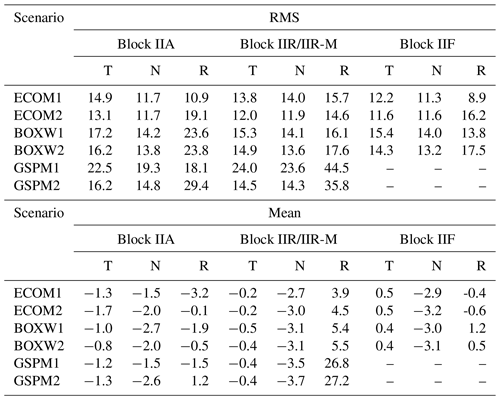
For all block types, the averaged orbit differences based on the six scenarios are almost around zero in every direction, except for those based on GSPM1 and GSPM2 for Block IIR/IIR-M in radial direction, which are 26.8 and 27.2 mm, respectively. One reason for the larger orbit differences for GSPM1/GSPM2 compared with IGS final orbits might be related to the fact: for nine Analysis Centers (ACs) contributing to the IGS final orbits (Villiger and Dach, 2019), the commonly adopted SRP strategies are ECOM parameterization with or without a priori models (e.g., box-wing model) and only final orbits of “jpl” from Jet Propulsion Laboratory (JPL) and of “emr” from Natural Resources Canada (NRCan) are based on GSPM.13 model with additionally estimated parameters (IGS, 2019; Springer et al., 2019). However, according to evaluation of SRP strategies done by Sibthorpe et al. (2011), the mean of minimum 1D RMS orbit differences w.r.t. the IGS orbits could reach 1.7 cm even with GSPM.04 and the improvement of orbit accuracy is not obvious for upgraded GSPM model (Sibois et al., 2014). Notice that the implementation of GSPM.04 by Sibthorpe et al. (2011) is different from what is done in this research. Besides of the a priori model, other parameter including the constant Y bias, the constant scale from the satellite to the Sun, stochastic variations for body-fixed Z and X axes as well as stochastic changes for y axis, are estimated in consideration of deficiency of a priori information. While in our study, the a priori model is used on top of ECOM parameterization. The incompatibility resulting from the different parameterization might be the reason for the larger orbit differences of GSPM1/2 w.r.t. IGS orbits, which is further discussed in Sect. 3.2.
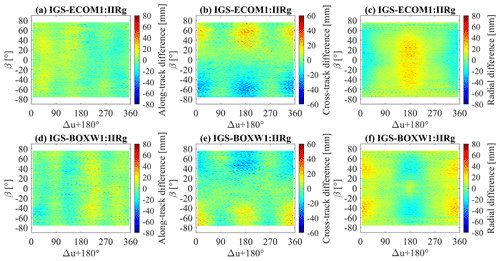
Figure 1Orbit differences between IGS and ECOM1 (a–c), IGS and BOXW1 (d–f) in along-track, cross-track and radial directions for Block IIR/IIR-M.
Another interesting thing to note is that for Block IIR/IIR-M satellites, even though little difference could be recognized between ECOM1 and BOXW1 in terms of the statistics of orbit differences w.r.t. IGS final orbits, the application of box-wing model do affect the determined orbit. The orbit differences between IGS and ECOM1 and orbit differences between IGS and BOXW1 versus Δu (here the is used as the horizontal coordinate so the reference zero-point is the midnight of the orbit) and the Sun elevation angle w.r.t. the orbit plane β, are shown in Fig. 1. As can be seen from the figure, the orbit differences show diametrically opposite patterns in three directions for two scenarios and this is especially obvious for cross-track and radial directions. In cross-track direction (see panels b and e), the orbits of IGS and ECOM1 are consistent except for the noon and midnight period with large β angle. When β is around 60∘, the orbit difference between IGS and ECOM1 is about 20 mm while that orbit difference is about −20 mm for β around . The orbits of IGS and BOXW1 show similar characteristics but the orbit differences are −20 and 20 mm, respectively, for β around 60 and . In radial direction (see panels c and f), the orbits of IGS and ECOM1 show about 20 and −20 mm differences, respectively, for noon and midnight period with β ranging from −60 to 60∘. However, the orbits of IGS and BOXW1 show about −20 mm difference for noon period with absolute β larger than 20∘ and less than 60∘ while the orbit difference for midnight period is about 20 mm with the same range of β. The similar level of orbit difference RMS but opposite orbit difference pattern for ECOM1 and BOXW1 compared with IGS indicate that based on the ECOM1 parameterization, the box-wing model could change the orbit dynamic characteristics of satellites without affecting the orbit consistency with IGS final orbits. This may also apply to other scenarios combining of different ECOM parameterizations and a priori information. Therefore, it is meaningful to investigate to what extent the a priori models affect the orbit in every orbital directions based on a special ECOM parameterization.
3.2 Detailed comparison of the different scenarios
Motivated by the result of Sect. 3.1, the orbit differences are evaluated with respect to Δu and β, in consideration of the relative geometry of the Sun, Earth and the GPS satellite in this part. Firstly, the orbits of ECOM1 and ECOM2, designated as “E1–E2”, are compared to reflect the effects of adjustment of ECOM parameters on GPS satellites. Based on the same ECOM parameterization, the orbits with and without a specific a priori model are then compared to assess the effects of the a priori model on GPS satellite orbits and the compatibility of an ECOM parameterization and an a priori model. The four comparison pairs “E1–B1”, “E1–G1”, “E2–B2” and “E2–G2”, represent the orbit comparison of ECOM1 and BOXW1, ECOM1 and GSPM1, ECOM2 and BOXW2, ECOM2 and GSPM2, respectively. Thus, we have five comparison pairs to analyze.
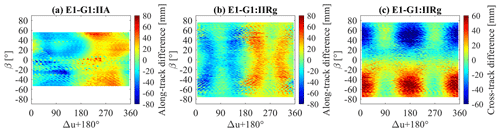
The radial orbit comparison results of five pairs listed above with respect to β and Δu ( is again taken as the horizontal coordinate) are discussed firstly owing to the abundant patterns for different block types (Fig. 2). The significantly different patterns of the first column suggest that the adjustment of ECOM parameters affects the estimated orbit differently for each block type. For Block IIA, a Fusiform (FF) pattern, showing largest positive difference more than 60 mm and negative difference less than −40 mm around noon and midnight, respectively, could be seen for β angles between −20 to 20∘. For Block IIR/IIR-M, a Peanut (PN) pattern, of which the β expands from −60 to 60∘, could be recognized in noon and midnight zone, with respectively largest negative difference of around −30 mm and positive difference of around 30 mm. For Block IIF, similar differences compared with Block IIR/IIR-M could be seen for β between −20 to 20∘, but when β is around zero degree, the orbit difference is negative from midnight to noon and positive from noon to midnight in the counterclockwise direction, causing a Dumbbells (DB) pattern. The largest negative-differences less than −60 mm arise post-midnight and before noon while positive-differences more than 60 mm arise post-noon and before midnight, where specific attitude control law is operated according to Dilssner (2010). The above results indicate that the adjustment from ECOM1 to ECOM2 brings differences related to Δu and β for orbit in radial direction and causes different patterns for various GPS block types, which is considered to be related to the special satellite geometry caused by mounted payload, like the W-sensor antenna for Block IIR/IIR-M satellites (Montenbruck et al., 2015), and attitude modeling errors, which are not completely compensable by the ECOM1 parameters. This is further discussed in consideration of the orbit differences introduced by the a priori model as follows.
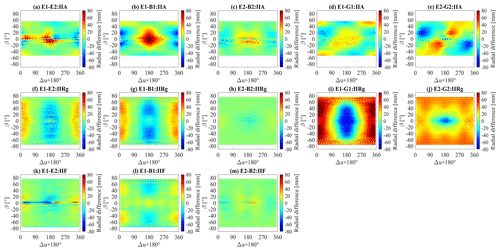
Figure 2Orbit differences of E1–E2, E1–B1, E2–B2, E1–G1, E2–G2 (from left to right) in radial direction for Block IIA (upper), Block IIR/IIR-M (middle), Block IIF (lower).
The effect of applying an a priori model based on the same parameterization could be seen according to the orbit difference patterns shown from the second column to the fifth column of Fig. 2. Firstly, the orbit differences for every a priori model are analyzed based on ECOM1, followed by analysis of orbits with the same a priori model based ECOM2 to assess the possible deficiency of ECOM1 and to what extent the new-added ECOM parameters could improve the performance.
In terms of the effects of box-wing model, BOXW1 mainly causes visible orbit differences in noon and midnight zone for three types of GPS satellites, as can be seen in the second column of Fig. 2. These differences should result from unmodeled or mis-modeled Z acceleration caused by SRP. It is worthwhile to note that only one constant parameter D0 is used to estimate direct SRP for ECOM1 parameterization and the radial direction coincides with body-fixed z-axis. Since the z-axis and eD are nearly perpendicular to each other for Δu equal to −90 or 90∘ and parallel to each other for Δu equal to 0 or 180∘ when the Sun is in the orbit plane. When there is an unmodeled or mis-modeled SRP acceleration related to z-axis, it reaches the maximum and minimum in noon and midnight or on the contrary in Z-direction, which could not be absorbed by the constant parameter in D direction. As a result, the orbit differences show the opposite pattern for noon and midnight zone. The range of β for the orbit differences of special block type during midnight and noon relies on the effective area contributing to the unmodeled acceleration and the orbit differences are gradually invisible with increase of β value owing to smaller projection of the Sun to Z-direction. Since the box-wing model is based on actual satellite shape, the above orbit differences should relate to the physical characteristics of the satellites, more precisely the special components contributing to the Z acceleration difference. For Block IIA, the Hamburger (HB) orbit difference pattern (panel b), of which the absolute difference could reach 60 mm compared with ECOM1, is most likely related to the large apogee engine and the flaring conical plume shield mounted on −Z panel, which is reported by Bar-Sever et al. (2009). The different optical properties of these components from those of +Z panel and possible shadowing effect due to the cone-shape cause the acceleration difference during noon and midnight, further leading to the orbit differences for the two periods. For Block IIR/IIR-M, the usage of the box-wing model in conjunction with ECOM1 parameters brings Peanut-like differences of around −30 and 30 mm (panel g) in noon and midnight zone, respectively, which is supposed to result from the W-sensor antenna mounted on ±X panels (Montenbruck et al., 2015), contributing 0.5 m2 to the ±Z areas (Rodríguez-Solano, 2014). For Block IIF, the situation is a little different: the orbit difference is generally small and a symmetric 7-Spots (7S) pattern of absolute difference 20 mm (panel l) could be observed for β around 50∘. The small difference implies that the SRP acceleration for ±Z panels are more consistent for Block IIF satellites compared with the other two types. The protruding component needing special treatment is the large auxiliary payload receive antenna (APRA) extending from the body-fixed −X panel. Since this panel is not radiated for Block IIF under nominal attitude, the acceleration caused by the APRA in radial direction is considered only for two conditions: (1) β is around zero when −Z panel is radiated (satellite is around the noon point) so that the back of APRA is not shaded by satellite bus since the APRA is close to +Z panel. (2) The Sun is above the orbit plane with a large β when +Z panel is radiated (satellite is around the midnight point) to avoid that the front of APRA is shaded by the Earth. Thus, the orbit differences of ECOM1 and BOXW1 could be observed when β is large enough for noon and midnight or β is around zero for noon. It is worthy to notice when satellites are in the shadow, the SRP acceleration derived from ECOM1 or BOXW1 should be zero and little orbit difference is supposed to observed, which is the case for Block IIA and Block IIF when absolute β is around 10∘ and below during midnight. However, for Block IIR the orbit difference in this period is still visible, which is unclear yet and needs further investigation. The above orbit differences introduced by box-wing model could be eliminated or mitigated with ECOM2 by adding new periodic terms in D direction, as shown in the third column in Fig. 2. For Block IIA, the previous orbit difference pattern is significantly weaken and absolute difference of 30 mm could only be observed when β is lower than 10∘. For Block IIR/IIR-M and IIF, there is little difference of orbits based on ECOM2 and BOXW2 (panels h and m). When reviewing the orbit differences of E1–E2 and E1–B1, it could be found that for Block IIA and IIR, the new parameters introduced in ECOM2 have a similar or even equivalent performance as the tested box-wing model, although the orbit differences for low β around noon and midnight, which is supposed to be related to the noon turn and midnight turn (Bar-Sever, 1996), cannot be eliminated by ECOM2 for Block IIA. As for Block IIF satellites, although the new periodic terms seem to perform differently from the box-wing model according to the orbit difference pattern, these ECOM parameters work with no conflicts with the box-wing model in terms of orbit consistency according to panel (m). The possible reason is although ECOM parameters are empirically derived and fail to reflect the physical background, these new parameters should be able to describe an “average” effect due to asymmetry of ±Z panels. Therefore, with BOXW2 the consistent orbits could be determined as with ECOM2 by adjusting the periodic parameters in D while losing the actual dynamic mechanism. For the GSPM model, there is no common characteristics for orbit difference pattern based on ECOM1 parameterization for two block types. GSPM1 causes orbit difference more than 20 mm in the diagonal position of plane compared with ECOM1 for Block IIA, designated as Diagonal (DG) pattern, which has the similarity as the pattern of E1–B1 during noon for low β only. However for Block IIR/IIR-M, using GPSM as a priori model causes generally positive differences and leads to the orbit differences like an Eye (EE), a strengthened Peanut pattern. This suggests that the GSPM model performs similarly in terms of orbit difference pattern compared with the box-wing model but the values of orbit adjustment of the two models are different for Block IIR/IIR-M satellites. When ECOM2 is used as the parameterization, a pattern consists of 4-Comets-like difference (4C) is observed for Block IIA and a Lips (LP) pattern arises for Block IIR/IIR-M. Since GSPM a priori information is empirically derived, it is difficult to explain the above special differences of E1–G1 and E2–G2 following physical clues and these particular patterns are supposed to result from incompatibility of GSPM a priori model and ECOM parameterization. This may also be the reason for the large orbit difference between IGS and GSPM1/2 for Block IIR/IIR-M discussed in Sect. 3.1. It is found the orbit difference patterns between IGS and GSPM1/2 in radial direction are quite the same as those between ECOM1 and GSPM1/2 presented in Fig. 2 (panels i and j). The large difference of absolute value 80 mm during noon and midnight for E1–G1 and general positive difference for E1–G1 as well as E2–G2, indicate that the use of the GSPM a priori model on top of ECOM parameterization model for IIR/IIR-M would bring a mean offset and large RMS in terms of radial orbit difference w.r.t. ECOM1/2. This is the same case for GSPM1/2 when compared with IGS, as has been showed in Table 1.
For orbit differences along the other two directions, there are another three typical patterns that could be classified, namely a 2-Bacons (2B), a Chromosome (CS) and a 6-Spots (6S) pattern as shown in Fig. 3. It should be noted that the first two patterns arising in along-track show reversed orbit differences in separate half-orbit-planes divided by connection-line of midnight point and noon point and the pattern found in cross-track shows opposite orbit differences for Sun positions above and beneath the orbit plane. These results indicate that two compared scenarios differ in modeling SRP in along-track and cross-track directions, which causes these patterns separated by noon-midnight line and orbit plane, respectively. The RMS and corresponding pattern types for every block type in each orbital direction are summarized in Table 2. If there is no obvious pattern, which suggests that both orbits are consistent in this direction, consequently no pattern type is given in Table 2. From the table it could be found that for radial direction, the orbit difference patterns are quite diverse while the CS pattern is common for orbit difference in along-track direction and the 6S pattern is often observed in cross-track direction for different types of satellites. It is very interesting to find that for Block IIR/IIR-M, any “upgrade” on ECOM1, like adding new ECOM parameters or introducing an a priori model, would cause the same orbit difference patterns in along-track and cross-track directions and similar orbit difference pattern in radial direction. This suggests that ECOM1 is insufficient to model SRP for Block IIR/IIR-M and ECOM2 should be a good candidate for this block type in consideration of the better consistency with an a priori model.
Table 2The RMS (unit: mm) and pattern types of orbit difference for the five compared pairs.
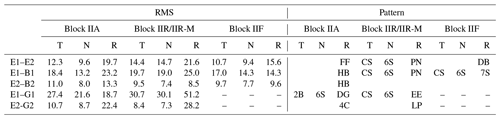
The pattern types and corrsponding abbreviations: 1. Fusiform (FF); 2. Chromosome (CS); 3. 6-Spots (6S); 4. Peanut (PN); 5. Dumbbells (DB); 6. Hamburger (HB); 7. 7-Spots (7S); 8. 2-Bacons (2B); 9. Diagonal (DG); 10. Eye (EE); 11. 4-Comets (4C); 12. Lips (LP).
According to Table 2 and the orbit difference patterns presented in Figs. 2 and 3, the following conclusions can be derived: (1) the two ECOM parameterizations show 10-20 mm orbit differences for GPS satellites in each direction of the orbit frame; applying the box-wing model or the GPSM.04 model cause 10–20 and 10–50 mm orbit differences, respectively, based on the specific ECOM parameterization. (2) The orbit differences resulting from different ECOM parameterizations and differences owing to the specific a priori model show Δu-related or β-related changes, especially in radial direction. These differences can be attributed to unique geometry of a block type, possible attitude regime and incompatibility of two combined models depending on the compared pair. (3) The orbits based on ECOM2 are more consistent with or without the tested a priori models than ECOM1. This is clearly related to the additional parameters in D direction, which performs quite the same as the box-wing model for Block IIR/IIR-M. For this block type, ECOM2 or BOXW1 have equivalent performance while for Block IIF, the additional periodic terms are not the same as box-wing model for radial direction in terms of orbit difference pattern. (4) For Block IIR/IIR-M satellites, the combination of GSPM.04 model with ECOM parameterization leads to large orbit difference compared with orbit based on the same ECOM parameterization without a priori model. And this incompatibility results in the large mean deviation of orbit difference between GSPM1/GSPM2 and the IGS.
In Sect. 3, the effect of applied a priori models on orbit determination was discussed. In this section, we investigate the effect of choice of a priori models on estimated ECOM parameters.
4.1 Statistical characteristics of ECOM parameters
For hybrid SRP strategies in this study, the total acceleration caused by solar radiation consists of two parts: (1) the a priori part derived from long-term observations fit (empirical a priori model) or based on the satellite-bus geometry, optical properties of the spacecraft etc. (analytical a priori model), and (2) the empirical part described with a set of specific parameters, which are used to fit the observations. Neglecting systematic perturbations caused by other forces, the estimated empirical parameters are expected to be zero if the a priori model perfectly characterizes the influence of the solar radiation. Thus, in this part, the parameters of two ECOM parameterizations are analyzed based on the six SRP scenarios described in Sect. 2, namely the ECOM1/2, BOXW1/2 and GSPM1/2.
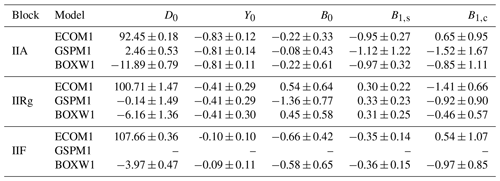
Table 3The mean and standard deviations of estimated parameters based on ECOM1 parameterization (unit: nm s−2).
4.1.1 ECOM1
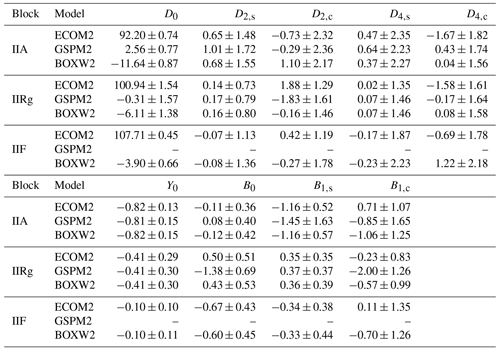
Table 3 shows the mean and standard deviations (SD) of estimated parameters based on ECOM1 parameterization and different a priori SRP strategies. As can be seen in the table, the parameter D0 differs a lot with different a priori SRP strategies and the use of an a priori model decreases the estimated value obviously as expected. Since the parameter D0 reflects the main constant acceleration from direct solar radiation, if this acceleration could be well derived from an a priori model, the parameter D0 would be close to zero. From the table it could be seen that GSPM.04 model performs better than box-wing model in terms of this constant acceleration. The estimated D0 based on GSPM.04 model is 2.46 nm s−2 for Block IIA and close to zero for Block IIR/IIR-M while those based on box-wing model for all block types are still pretty large considering the magnitude of SRP, especially for Block IIA. These large estimates of D0 indicate the deficiencies of the a priori SRP models. The mean of parameter Y0 is highly consistent with small SD even based on different a priori SRP strategies for a special block type, which could be explained by the fact that generally the vector of sunlight is perpendicular to the normal vector of Y panels when satellites are under nominal yaw attitude. Thus, the acceleration owing to the irradiated part of Y component is quite small and would change only slightly even if an a priori SRP model were considered for this component. The estimated values of parameter B1,c show visible differences when different a priori strategies are adopted for all block types. For the other two parameters in B direction, the characteristics are different for various block types. The parameter B0 estimated for Block IIA differs slightly from each other if a different a priori SRP strategy is adopted. The use of box-wing model causes only small differences for parameters B1,s while adoption of GSPM.04 model changes this parameter obviously and the reason needs to be further investigated. Different from Block IIA satellites, the adoption of any a priori SRP model has little effect on the parameter B1,s for Block IIR/IIR-M. Besides, the use of GSPM.04 model would lead to the obvious change for parameter B0. For IIF satellites, the box-wing model has small effect on the parameter B0 while it makes little difference for the parameter B1,s compared with the no a priori SRP model condition.
4.1.2 ECOM2
Table 4 shows the mean and SD of estimated parameters based on ECOM2 parameterization and different a priori SRP strategies. For parameters in D direction, the values of parameters D2,c and D4,c, similar to parameter D0, seem to be related to the a priori SRP strategy for all block types. However, the estimates of the other two parameters D2,s and D4,s are stable for a special block type based on different a priori SRP strategies, D2,s based on GSPM.04 model for Block IIA excluded. The stability of these two parameters despite different a priori SRP strategies might suggest that (1) these two parameters are related to modeling deficiency of other forces, like unmodeled along-track perturbation, rather than solar radiation or (2) the information of tested a priori SRP models are not adequate to model part of SRP related to these two parameters. This needs to be further investigated. The ranges of the parameter Y0 for different types of satellites show similar characteristics as that based on ECOM1 parameterization for the same reason. As for parameters in B direction, the introduction of any a priori SRP model affects the estimated value of B1,c but only the use GSPM.04 model changes obviously the estimated value of parameter B0 for IIRg satellites and that of parameter B1,s for IIA satellites.By comparing the results of Tables 3 and 4, it could be found that standard deviations of parameter D0 are quite different between block types but for the same block type, the SDs based on different SRP scenarios, ECOM1 for Block IIA excluded, are highly consistent. Notice that this parameter is estimated as a daily constant, the standard deviation of D0 reflects the variation of D0 w.r.t. the Sun elevation angle β as β changes slowly on one-day scale. For GPS satellites under nominal attitude, the radiated panel varies among body-fixed ±Z and +X (−X for Block IIR/IIR-M). Although with a priori information or new added periodic terms, the SRP effects caused by asymmetry of the satellite bus could be partly modeled, there are left asymmetrical effects related to the angle β since the projection area perpendicular to the direct sunlight also depends on this angle. Thus, the larger SDs of D0 for Block IIR/IIR-M indicate that the properties of the radiated three panels of these block types should be less consistent compared with ones of the Block IIA and Block IIF.
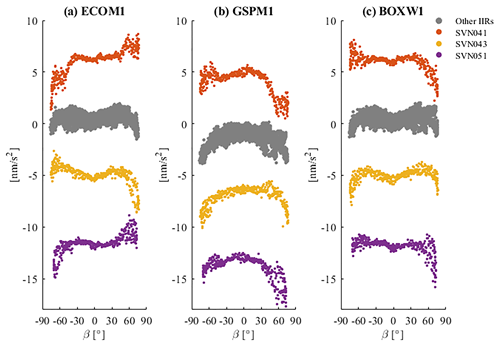
Figure 4Estimated parameters B0 based on ECOM1, GSPM1 and BOXW1 for Block IIR/IIR-M satellites. The parameters B0 of SVN041, SVN043 and SVN051 are shifted 6, −6 and -12 nm s−2 w.r.t. original value.
4.2 Block IIR satellites with obvious asymmetry
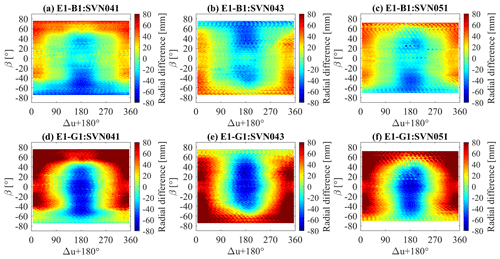
The acceleration resulting from SRP relates to factors which change rapidly on a timescale equivalent to the orbit, such as the Earth-satellite-Sun angle (E) and the attitude of the spacecraft. It also depends on other slower factors such as the solar irradiance and aging effects on the satellites, which we consider to be constants. Considering two epochs when a satellite runs to the same position of its orbit (i.e., same Δu) in nominal attitude, while β at these two epochs are the same in absolute sense but with opposite sign, we expect the same angle E since the orbit height of GPS satellites are far less than the distance between the Sun and the Earth, and approximately we have cos E=cos βcos Δu (Bar-Sever, 1996). This means that the angles between vector eD and body-fixed z-axis are the same for two epochs. Notice the vector eD and body-fixed y-axis is perpendicular in nominal attitude, namely the angles between eD and body-fixed y-axis are also the same for two epochs. Therefore, for a symmetric satellite with the same optical properties for two opposite surface panels, the area of the irradiated zones are the same and it is expected that the acceleration caused by solar radiation should be equivalent for the two epochs. This also applies to parameters of ECOM since the y-axis of DYB frame is parallel to the y-axis of body-fixed frame and the transformation remains constant. However, in the ECOM parameter analysis based on different SRP scenarios, it is found that for some Block IIR satellites, the estimated parameters in B show obviously an asymmetry w.r.t. the angle β. As presented in Fig. 4, the estimated parameter B0 of most IIR/IIR-M satellites shows an “M” pattern w.r.t. β, while the same parameter of GPS satellites SVN041, SVN051 rise up and that of SVN043 declines with the increase of β for ECOM1 (Fig. 4a). If an a priori model is applied, this asymmetry gets mitigated but is still visible for large β angle (Fig. 4b and c). This asymmetry is also found in the parameter B1,c and it shows the same increasing or decreasing behavior for a specific satellites as B0. For B1,s, however, the asymmetry is not visible. So for ECOM1, this would cause the large difference for acceleration in direction B when β is large with positive and negative sign, which implies the asymmetry of the +X and the −X panels. The asymmetry of parameters in B is not found for scenarios with ECOM2 parameterization, and this might be explained by the newly added 2pr and 4pr parameters in D direction, which absorb the unmodeled asymmetry error existing in ECOM1.
It should be noted that the introduction of a priori acceleration changes the form for B0 (also for B1,c) with respect to β (Fig. 4b and c) by reducing the asymmetry (for SVN041 and SVN051) or even leading to almost symmetric pattern (for SVN043). This means the acceleration related to asymmetrical properties could be modeled or partly described with the two a priori models thus the asymmetrical characteristics of parameters in B direction are weakened. If adjusting parameters in B direction for scenario ECOM1 has the similar performance to describe the asymmetry as a priori information of GSPM1/BOXW1, it would be expected the determined orbits are consistent for ECOM1 with or without a priori model, which, however, is contrary to the reality. The Fig. 5 shows the radial orbit comparison of ECOM1 and GSPM1/BOXW1 for the three GPS satellites considered here. Obviously the orbit differences show significant asymmetry and opposite value when absolute β is about 60∘ and larger. Notice the fact that when the Sun is in the position for a large β angle, the angle between vector of radial and vector eB is rather small and radial orbit differences are strongly related to acceleration in direction B. Therefore, we can derive that these asymmetric orbit differences owe to (1) the deficiency of ECOM1 parameters to model the asymmetrical properties of the satellites (assume a priori information is accurate to describe), (2) the mis-modeling of a priori information which could not be compensated by the ECOM1 parameters or (3) the combination of both. For any of the three possibilities, this indicates that the ECOM1 is not sufficient to compensate asymmetrical errors from a priori model nor to parameterize satellites with asymmetrical properties.
In this paper, we evaluated the effect of two a priori models and a no a priori model case based on two ECOM parameterizations on the orbit differences and estimated ECOM parameters for GPS satellites. The orbit comparison with IGS final orbits shows that the orbit consistency of ECOM1, ECOM2, BOXW1 and BOXW2 with IGS product is about 20 mm while that for GSPM1 and GSPM2 could reach 50 mm for Block IIR/IIR-M satellites. Orbits derived with six different scenarios for SRP modeling are then compared in this way: ECOM1 and ECOM2 are compared to assess the effect of changing the ECOM parameterization on precise orbit determination and differences between GSPM1/BOXW1 and ECOM1, GSPM2/BOXW2 and ECOM2 are investigated to evaluate the a priori model's influence on the precise orbits. It is found that the differences caused by changing the ECOM parameterization and by applying an a priori model mainly result in radial orbit differences, and these orbit differences are obviously larger at noon and midnight period especially when the Sun is around the orbit plane. Nine typical orbit difference patterns in radial direction and three typical orbit difference patterns in along-track and cross-track are classified for different comparison pairs with orbit difference RMS of each. The analysis of estimated ECOM parameters shows that applying an a priori model decreases the estimated value of parameter D0 for ECOM1 and ECOM2 dramatically. The parameters D2,c and D4,c in ECOM2 are sensitive to the a priori models while D2,s and D4,s are more stable for a specific block type with different a priori SRP model strategies. The values of the three parameters in B directions depend on both block types and a priori strategies. The estimated parameters in B direction for ECOM1 show asymmetric characteristics w.r.t. the elevation of the Sun (β) for SVN41, SVN43 and SVN51. This asymmetry related to the X panels could be improved to some degree applying GSPM.04 or box-wing model. The corresponding asymmetry of orbit differences observed in radial direction for large β, which is not found for ECOM2, shows that ECOM1 is insufficient to parameterize the solar radiation pressure for non-symmetrical spacecrafts. It is interesting to point out that the three satellites showing the different asymmetry in B are divided into three sub-groups of Block IIR-A/B satellites according to Sibois et al. (2014). In their research, a special coefficient of the GSPM model is used to sort the satellites, which inspires that a set of coefficients of ECOM might also be helpful to classify the satellites within the same block type according to their differences in geometry or other properties of spacecraft. Besides, the connection of a priori model and the parameters of ECOM is expected to be further investigated for other systems like BeiDou, Galileo and GLONASS to optimize the current a priori model or develop a new one for a special system.
The data used for this work are publicly and freely available on the IGS global data centers (https://www.igs.org/data-access/#data-centers, Johnston et al., 2017).
XC, BM designed the study. XC carried out the comparison and data analysis. All authors contributed to the interpretation and discussion of the results. XC prepared the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
This article is part of the special issue “European Geosciences Union General Assembly 2020, EGU Geodesy Division”. It is a result of the EGU General Assembly 2020, 4–8 May 2020.
We would like to thank the International GNSS Service for providing GNSS data and products. The comments and suggestions from the three anonymous reviewers are greatly appreciated.
This research has been supported by the China Scholarship Council (grant no. 201703170248).
The article processing charges for this open-access publication were covered by the Helmholtz Centre Potsdam – GFZ German Research Centre for Geosciences.
This paper was edited by Mathis Bloßfeld and reviewed by three anonymous referees.
Arnold, D., Meindl, M., Beutler, G., Dach, R., Schaer, S., Lutz, S., Prange, L., Sośnica, K., Mervart, L., and Jäggi, A.: CODE's new solar radiation pressure model for GNSS orbit determination, J. Geod., 89, 775–791, https://doi.org/10.1007/s00190-015-0814-4, 2015. a, b, c, d
Bar-Sever, Y. E.: A new model for GPS yaw attitude, J. Geod., 70, 714–723, https://doi.org/10.1007/BF00867149, 1996. a, b, c
Bar-Sever, Y. E. and Kuang, D.: New empirically derived solar radiation pressure model for global positioning system satellites during eclipse seasons, IPN Progress Report, 42–159, available at: https://ipnpr.jpl.nasa.gov/progress_report/42-159/159I.pdf (last access: 10 May 2021), 2004. a, b, c
Bar-Sever, Y. E. and Russ, K. M.: New and improved solar radiation models for GPS satellites based on flight data, Tech. rep., Jet Propulsion Laboratory, California Institute of Technology, Pasadena, USA, available at: https://apps.dtic.mil/sti/pdfs/ADA485820.pdf (last access: 10 May 2021), 1997. a, b, c
Bar-Sever, Y. E., Davis, J., Dach, R., Flohrer, C., Herring, T., Ray, J., Slater, J., and Thaller, D.: Impact of SLR tracking on GPS, in: ILRS Workshop on SLR tracking of GNSS constellations, Metsovo, Greece, available at: https://cddis.nasa.gov/metsovo/docs/PP01_SPRINGER_GPS.pdf (last access: 10 May 2021), 2009. a
Beutler, G., Brockmann, E., Gurtner, W., Hugentobler, U., Mervart, L., Rothacher, M., and Verdun, A.: Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamics (IGS): Theory and initial results, Manuscr. Geod., 70, 367–384, 1994. a
Dilssner, F.: GPS IIF-1 satellite, antenna phase center and attitude modeling, Inside GNSS, 5, 59–64, available at: https://www.insidegnss.com/auto/sep10-Dilssner.pdf (last access: 10 May 2021), 2010. a, b
Fliegel, H., Gallini, T., and Swift, E.: Global positioning system radiation force model for geodetic applications, J. Geophys. Res.-Sol. Ea., 97, 559–568, https://doi.org/10.1029/91JB02564, 1992. a, b
Fliegel, H. F. and Gallini, T. E.: Solar force modeling of block IIR global positioning system satellites, J. Spacecr. Rockets, 33, 863–866, https://doi.org/10.2514/3.26851, 1996. a, b
IGS: Analysis Center Processing Strategies, available at: https://kb.igs.org/hc/en-us/articles/201971713-Analysis-Center-Processing-Strategies (last access: 30 June 2020), 2019. a
Johnston, G., Riddell, A., and Hausler, G.: The International GNSS Service, in: Springer handbook of global navigation satellite systems, edited by: Teunissen, P. and Montenbruck, O., Springer International Publishing, Cham, Switzerland, 967–982, https://doi.org/10.1007/978-3-319-42928-1_33, 2017 (data available at: https://www.igs.org/data-access/#data-centers, last access: 20 May 2021). a, b
Kouba, J.: A simplified yaw-attitude model for eclipsing GPS satellites, GPS Solut., 13, 1–12, https://doi.org/10.1007/s10291-008-0092-1, 2009. a
Männel, B., Brandt, A., Nischan, T., Brack, A., Sakic, P., and Bradke, M.: GFZ rapid product series for the IGS, GFZ Data Services, https://doi.org/10.5880/GFZ.1.1.2020.003, 2020. a
Montenbruck, O., Schmid, R., Mercier, F., Steigenberger, P., Noll, C., Fatkulin, R., Kogure, S., and Ganeshan, A. S.: GNSS satellite geometry and attitude models, Adv. Space Res., 56, 1015–1029, https://doi.org/10.1016/j.asr.2015.06.019, 2015. a, b, c
Rodríguez-Solano, C. J., Hugentobler, U., and Steigenberger, P.: Adjustable box-wing model for solar radiation pressure impacting GPS satellites, Adv. Space Res., 49, 1113–1128, https://doi.org/10.1016/j.asr.2012.01.016, 2012. a, b, c, d, e
Rodríguez-Solano, C. J.: Impact of non-conservative force modeling on GNSS satellite orbits and global solutions, PhD thesis, Technische Universität München, Germany, available at: https://mediatum.ub.tum.de/doc/1188612/719708.pdf (last access: 10 May 2021), 144 pp., 2014. a
Sakumura, C., Sibois, A., Sibthorpe, A., and Murphy, D.: Improved modeling of GPS block IIF satellites for the GSPM13 solar radiation pressure model, in: IGS Workshop, Paris, France, 2017. a, b
Sibois, A., Selle, C., Desai, S., Sibthorpe, A., and Weiss, J.: GSPM13: an updated empirical model for solar radiation pressure forces acting on GPS satellites, in: IGS Workshop, Pasadena, USA, available at: https://www.researchgate.net/publication/283517257_GSPM13_An_Updated_Empirical_Model_for_Solar_Radiation_Pressure_Forces_Acting_on_GPS_Satellites (last access: 10 May 2021), 2014. a, b, c, d
Sibthorpe, A., Weiss, J., Harvey, N., Kuang, D., and Bar-Sever, Y.: Empirical modeling of solar radiation pressure forces affecting GPS satellites, in: AGU Fall Meeting, San Francisco, USA, available at: http://acc.igs.org/orbits/srp-models_JPL_agu10.pdf (last access: 10 May 2021), 2010. a, b
Sibthorpe, A., Bertiger, W., Desai, S. D., Haines, B., Harvey, N., and Weiss, J. P.: An evaluation of solar radiation pressure strategies for the GPS constellation, J. Geod, 85, 505–517, https://doi.org/10.1007/s00190-011-0450-6, 2011. a, b
Springer, T., Beutler, G., and Rothacher, M.: A new solar radiation pressure model for GPS, Adv. Space Res., 23, 673–676, https://doi.org/10.1007/PL00012757, 1999. a
Springer, T., Dach, R., and Sibthorpe, A.: GNSS orbit RPR model considerations, in: Proceedings of International GNSS Service: Analysis Centre Workshop, Potsdam, Germany, available at: http://igs-acc-web.s3.amazonaws.com/igs-acc-website/workshop2019/Orbit_PosPaper.pdf (last access: 10 May 2021), 2019. a
Villiger, A. and Dach, R.: International GNSS Service Technical Report 2018 (IGS Annual Report), Tech. rep., IGS Central Bureau and University of Bern, Bern Open Publishing, https://doi.org/10.7892/boris.130408, 2019. a
GPS space segment: https://www.gps.gov/systems/gps/space/ (last access: 5 June 2020)
GFZ Analysis Strategy Summary: https://files.igs.org/pub/center/analysis/gfz.acn (last access: 15 March 2021)