Regional hydraulic model of the Upper Rhine Graben
Nora Koltzer
Magdalena Scheck-Wenderoth
Mauro Cacace
Maximilian Frick
Judith Bott
In this study we make use of 3-D hydraulic simulations to investigate the regional groundwater flow in the Upper Rhine Graben. The modeling is based on an existing detailed 3-D structural model covering the whole Upper Rhine Graben from the surface down to 14 km of depth. The overall goal of this study is to provide some quantitative analysis on the role of the hydraulic head topology in shaping the underground hydrodynamics by taking into account interactions with the heterogeneous subsurface sedimentary configuration of the basin system. Therefore, the main question addressed by this study can be summarized as follows: does the deep graben flow follow the topographic gradient and the flow direction of the river Rhine from the Alps northward to the northernmost area of the Upper Rhine Graben?
Our results demonstrate the presence of a regional subsurface flow in the sedimentary rocks aligning from the graben flanks towards its center and in the southern half of the graben from south to north. The graben-parallel flow velocity is found to be about 1 order of magnitude lower than the velocity predicted perpendicular to the main graben axis. Besides these general trends, the modeling highlights local heterogeneities in the shallow 3-D flow field. Those arise from the interaction between regional groundwater flow and the heterogeneous sedimentary configuration. Within the Cenozoic sediments forming the uppermost aquifer in the model, groundwater flows are driven by imposed hydraulic gradients from recharge areas located at higher elevations in the Black Forest and Vosges Mountains to the discharge region at a lower elevation in the Rhine valley. The presence of a regional aquitard (Keuper) separating the shallow and the deeper aquifer system (Muschelkalk, Buntsandstein, and Rotliegend) hinders hydraulic connection among the two aquifer systems. This is exemplified by the development of a flow system in the deeper aquifers, which shows a more continuous graben-parallel south–north direction. Based on these results we can conclude that both the hydraulic head topology and the level of structuration of the sedimentary sequence exert a 1st-order role in shaping the regional flow system at depth. The regional model predicts a heterogeneous flow system within the upper 4 km of the Upper Rhine Valley, where flow velocities in the graben valley can reach up to 45 mm yr−1 in the upper and lower aquifers. Back to the current conceptual hydrogeological model, the results question the presence of a graben through northward flow, being limited to the southern half of the graben. In the north, the groundwater dynamics turn out to be more complex, being structurally linked to the local geology. This calls for additional studies with a higher level of both structural and stratigraphic attributes in order to arrive at a better quantification of the local to the regional groundwater dynamics in the area.
- Article
(18880 KB) - Full-text XML
- BibTeX
- EndNote
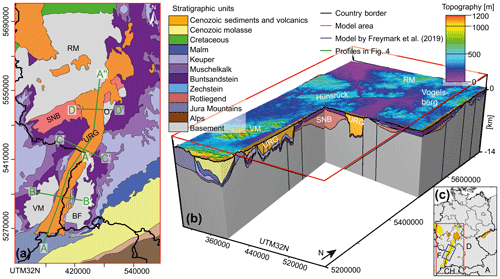
Figure 1(a) Geological map modified after BGR (2014) of the model area; (b) structural model (after Freymark et al., 2017) used as a base for the numerical model; (c) overview map of model area in red and of previous work by Freymark et al. (2019) in blue. RM: Rhenish Massif, SNB: Saar–Nahe Basin, O: Odenwald, VM: Vosges Mountains, BF: Black Forest (changed according to Freymark et al., 2017). The URG is limited by border faults along its eastern and western margins that are represented as lateral changes in the bordering lithologies but not considered distinct features in the structural model.
The motivation behind this study is rooted in the search to quantify the intrinsic connection between the productivity of hydrothermal wells and the hydraulic conditions affecting the reservoir hosting the targeted resources. In order to achieve this goal, we demonstrate here that regional-scale (i.e., basin-wide) fluid flow models are a basic requirement prior to any exploitation strategy. Such models, integrating the regional geology and physics, are essential to understand the hydraulic conditions acting on the basin scale. The hydraulic conditions at that scale of the whole system provide the natural forcing exerted on the reservoirs (Frick et al., 2016; Noack et al., 2013).
The study area is the Upper Rhine Graben (URG hereafter), a still active rift developed during Eocene times by transtensional reactivation of the European Cenozoic Rift (Dèzes et al., 2004). With respect to the regional hydrodynamics, previous studies have identified the URG as a regional discharge valley. The main recharge is thought to occur along the graben flanks (Black Forest, Vosges Mountains and Odenwald) with groundwater discharging preferentially within the graben itself (Clauser and Villinger, 1990; Freymark et al., 2019; Guillou-Frottier et al., 2013; Lampe and Person, 2002; Pribnow and Clauser, 2000). Indeed, the deepest topographic point (also the lowest elevation of the hydraulic head) is found in the northern domain within the federal state of Hesse. Based on these observations, it is likely that the regional flow, as driven by hydraulic head gradients, is characterized by a dominant south-to-north component. This said, a physical-based quantification of this conceptual model has never been done. Therefore, in this study we aim to address the following basic questions: (a) what is the regional hydraulic configuration of the whole URG? (b) Does the deep fluid flow follow the shallow surface hydrodynamics as driven by the water table topology, or are those systems hydraulically disconnected? And to what degree?
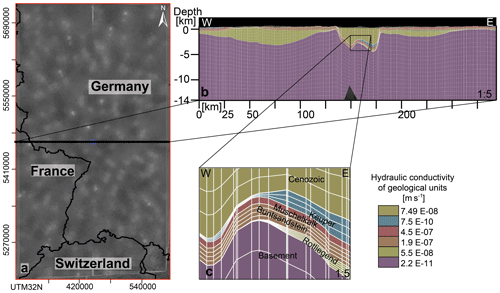
To answer these questions we investigate the regional fluid flow within the URG, relying on a regional hydraulic model covering the entire URG. The structural model is based on an up-to-date detailed geological model (Freymark et al., 2017) limited here to 14 km of depth (Fig. 1), assuming this geological boundary is acting as a no-flow boundary. The finite-element model has been built within the commercial software FEFLOW© (Diersch, 2014); more information is given in Sect. 2. For more details about the structural modeling and the geological database used as input data, we refer to Freymark et al. (2017, 2015). It is worth mentioning that the input model integrates all available data as well as earlier modeling results and therefore provides a geologically consistent base for our numerical investigations on the shallow and deep fluid flow circulation dynamics with respect to their driving force. Given our scientific goal, and in order to minimize sources of uncertainties in the modeling studies, we neglect temperature, salinity, and mechanical effects, therefore solving only a hydraulic problem. The rationale behind our choice stems from the fact that it allows for the quantification of the pure pressure-driven regional fluid flow dynamics. These are in response to variations in hydraulic head gradients and variations in the subsurface hydraulic conductivity field.
As discussed in the Introduction, the input structural model integrates available seismic data, field and well observations, and published depth and thickness maps, and it assembles the information from previously published 3-D structural models (more detail in Freymark et al., 2017). The base of the model was limited to 14 km of depth assuming that the upper crust at that depth is hydraulically impermeable and that the fluid flow should be negligible at those depths (Fig. 1a). Data from groundwater measurements (BRGM, 2016; Herrmann, 2010; LUBW, 2016a, b) were integrated to determine an observation-based hydraulic head (imposed as a fixed upper boundary condition in the simulations), while the range of variations of hydraulic parameters was inferred from literature data (Table 1).
2.1 Numerical model setup
The modeling carried out is based on the assumption of fluid flow under steady-state conditions. The boundary conditions were set at all six borders: at the top and bottom and at the four vertical boundaries. The four vertical (south, west, north, and east) and the bottom model boundaries are closed to fluid flow (essential Neumann boundary condition). As an upper boundary condition a Dirichlet constant head is imposed based on hydraulic head measurements (black dots in Fig. 2). With this type of boundary condition the hydraulic head is fixed at each node at the top of the model, and inflow and outflow (recharge and discharge) are therefore allowed. In some areas of high topographic relief (e.g., Vosges Mountains, Jura Mountains, Alps, Black Forest, Hunsrück) the paucity of available data required us to rely on a certain degree of approximation by smoothing the topography at the highest elevations as a subdued replica of the groundwater surface (Fig. 2). In the Alps we fixed the groundwater surface to 100 m below the topography.
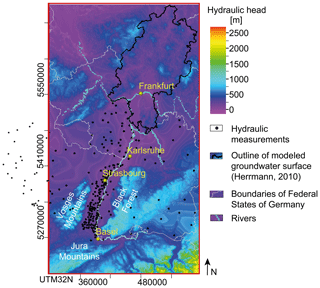
Figure 2Applied upper Dirichlet boundary condition (BC) with input data for the interpolation in black (LUBW, 2016a, b; BRGM, 2016; Herrmann, 2010). Hydraulic head with respect to mean sea level.
Following our modeling assumption, the distribution of Darcy velocities (qf) is obtained by solving for the Darcy equation and fluid mass balance considerations, which under steady-state conditions reads as follows:
with K being the hydraulic conductivity tensor (m s−1) and h the hydraulic head (m). The hydraulic conductivities are derived based on literature data (Table 1). All geological units are parameterized as homogeneous in their hydraulic parameters, therefore assuming the isotropic distribution of properties within each geological unit, and we do not account for nonlinear feedbacks from variations in the fluid properties, mainly fluid density and viscosity variations.
Table 1Physical input property hydraulic conductivity (K; m s−1) for each geological unit. Values derived from (a) Bär (2012), (b) Lampe and Person (2002), (c) Jodocy and Stober (2011), (d) GeORG-Projektteam (2013a), (e) Clauser and Villinger (1990), (f) Stober and Bucher (2015), (g) LfU (2007), (h) Przybycin et al. (2017), (i) GeORG-Projektteam (2013b), (j) Stober and Jodocy (2009), and (k) GeORG-Projektteam (2013c).
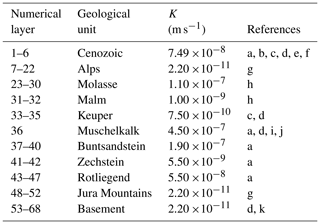
The numerical model comprises 11 geological units resolved by 68 numerical layers. The number of numerical layers has been imposed to ensure numerical stability (Fig. 3). The unstructured mesh consists of 6 736 896 tetrahedral elements. The model size is approximately 500 km in the south–north direction, 300 km in the west–east direction, and 14 km in vertical depth.
We discuss the modeling outcomes based on specific profiles (their locations are shown by the green lines in Fig. 1): one cutting the graben parallel to its axis, while the other cross sections are perpendicular to the graben axis, with one located in the south, one in the center, and the last one in the north of the study domain.
A general feature common to all hydraulic head profiles is that the graben-perpendicular hydraulic head gradients (Fig. 4b–d) are stronger than those along the graben axis (Fig. 4a), mainly reflecting the topology of the groundwater head distribution used to impose the upper boundary condition (Fig. 2). Another observation that holds true for all investigated sections is the influence of the Keuper aquitard on the flow field; the latter is schematized in white in Fig. 4e. The flow in the deeper aquifers (pre-Keuper sequence) aligns according to the top of the crystalline basement. In contrast, the groundwater flow in the upper aquifers is decoupled from that observed at greater depth, being mainly driven by surface hydraulic head gradients. Hydraulic decoupling along the two regional aquifers is indicated by an inflection in the isolines of hydraulic heads in the places where the Keuper aquitard is present.
The hydraulic head distribution across the URG varies while moving from the southern to the northern domain. The Black Forest (groundwater head up to 1.2 km) to the east, the Jura Mountains (groundwater head up to 1.3 km) to the south, and the Vosges Mountains (groundwater head up to 1.25 km) to the west confine the groundwater flow around the southern URG. The hydraulic head gradient from the Vosges Mountains and the Black Forest to the center of the URG is approximately 2.5 m per 100 m. On the other hand, the gradient from the Jura Mountains to the lowest elevation point in the URG in the north amounts to only 0.3 m per 100 m (integrated over the whole length of the URG). Hydraulic head gradients perpendicular to the graben axis are about 7 times higher in magnitude in the southern part of the URG than the graben-parallel gradients. This is reflected by the modeled fluid flow, which shows a preferential component infiltrating from the graben shoulders into the graben itself. However, the magnitudes of hydraulic gradients vary along the graben. These gradients are highest in the southern domain (Fig. 4b), lowest in the central part (Fig. 4c), and moderate in the northern part of the URG (1.6 m per 100 m from the Odenwald recharge area to the graben center; Fig. 4d). The head gradient perpendicular to the graben axis in the central part of the URG is around 0.2–0.5 m per 100 m and 3 times higher than the parallel gradient, which is about 0.08 m per 100 km between Strasbourg and Heidelberg.
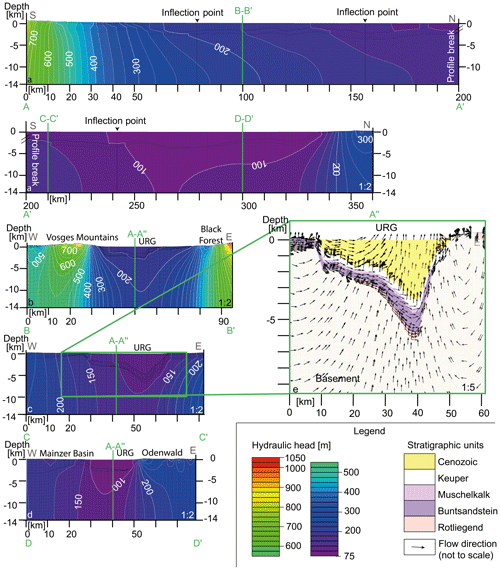
Figure 4Simulated hydraulic head distribution (a–d). Colors from purple to red and white isolines show hydraulic head variations in 25 m fringes. Profiles cross-cutting the URG axis (a) along the URG from south to north, with a profile break after 200 km, and perpendicular to the graben (b) in the south from the Vosges Mountains to the Black Forest; (c) in the central part of the URG and (d) in the northern part from the Mainzer Basin to the Odenwald. The locations where profiles intersect are marked with vertical green lines. All profiles are 2 times vertically exaggerated. Figure (e) illustrates a zoom of the profile in panel (c) with 5 times vertical exaggeration; the colors represent geological units, and the non-scaled black arrows represent flow directions. All profile locations are shown in Fig. 1a.
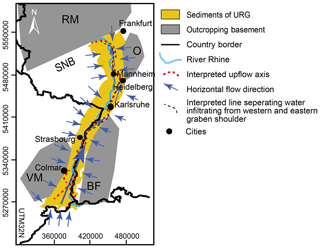
To illustrate the 3-D fluid flow across the study area we make use of distinct maps on which we plot the x, y, and z component of the flow vector (Fig. 5). These were calculated for the entire model domain and are illustrated by a top-view projection on the model with the highest flow values in the brightest colors. By separating each component, we obtain a quasi-3-D analysis of the groundwater flow dynamics. In Fig. 5a and 5d a clear hydraulic separation (highlighted by a black stippled line) occurs with the river Rhine, acting as a natural divide between the western and eastern graben areas. The graben flanks act as a major recharge, leading to a graben-perpendicular flow towards the graben center. This pattern is consistent over the whole URG.
Going back to the main working hypothesis of this study, that is, whether or not the regional fluid flow follows a preferential south-to-north axis over the whole study area, we systematically discuss in the following the results based on the y component of the flow vector (Fig. 5b and e). At a first glance, our results provide a more complex flow field than conceptually thought. In the south, approximately up to the city of Strasbourg, the fluid flow shows a general northward trend in line with the current conceptual model (orange in Fig. 5b). This regional component changes while moving towards the central part of the graben, between Strasbourg and Heidelberg. There, groundwater flows preferentially towards the east of the graben. Consequently, the divide between recharge from the western and recharge from the eastern graben shoulder and the axis of ascending water also shift to the eastern side of the graben, thereby deviating from the expected natural discharge conceptualized to coincide with the river Rhine (Fig. 5c). The reason for this deviation is related to the topography of the top Variscan basement. In the area around the city of Karlsruhe, the top of the Variscan crust reaches its deepest depth at the eastern graben border. Therefore, fluid coming from the western and the southern domains is channeled into this depression. Based on this result, we can conclude that the geological configuration of the deeper sedimentary compartments exerts a 1st-order influence on the resulting groundwater dynamics in this region.
The northern part of the URG, between Mannheim and Frankfurt, is characterized by an even more complex flow regime lacking a dominant northward flow direction, though groundwater still ascends below the river Rhine. This requires a revision of the groundwater flow dynamics that, despite showing a south–north flow component, is locally overprinted by a small-scale circulation, leading to the occurrence of a heterogeneous flow field. In this region, the main flow component is provided by water recharging from the western and eastern graben shoulders (Figs. 4d and 5a). Moreover, the top of the basement in the northernmost part of the graben dips southward, thus imposing a north-to-south-oriented preferential direction to the flow.
Comparing the results obtained for the northern and the southern domains, we can identify hydrodynamics that share some characteristics, while being diverse overall. On a graben-wide scale, the recharge is from the graben shoulders to the graben center. This fluid flow component, perpendicular to the graben axis, is mainly present in the upper aquifer (post-Keuper sequence). It is driven by higher hydraulic gradients perpendicular to the URG than those parallel to the graben axis. However, the groundwater dynamics in the southern domain show a rather homogeneous character with consistent northward flow, which contrasts the one occurring further north. There, groundwater flow is controlled by the top of the basement deepening to the south, leading to a preferential north–south flow direction, which is therefore opposite to the dynamics imposed by topographic gradients.
Outside the URG area, predicted fluid flow patterns resemble the surface hydraulic head distribution, with infiltration in the Alpine region and pronounced fluid uprising in the bordering valleys (Fig. 5). Infiltration is also predicted to occur beneath the Black Forest and Vosges Mountains in response to elevated hydraulic gradients. For the latter, inflow occurs radially with a weak E–W component, while the inflow axis in the Black Forest is oriented SSW–NNE (Fig. 5).
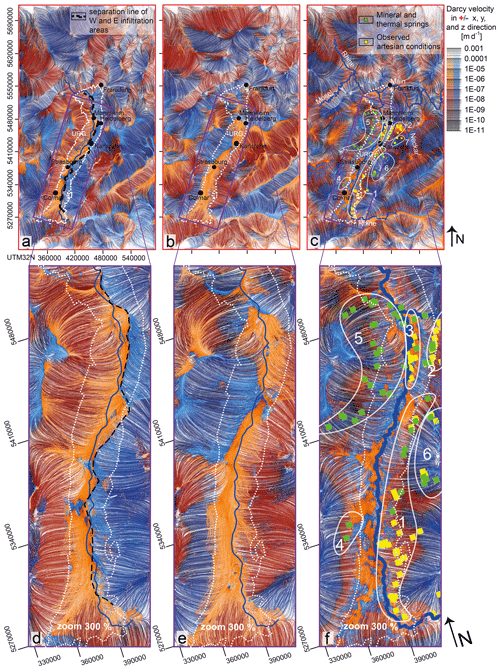
Figure 5Streamlines of simulated fluid flow with different colors for the x, y, and z component of the flow vector. (a) The west–east (x) component, (b) north–south (y) component, and (c) vertical (z) component of the flow vector. In orange is the positive (east, north, and ascending) component and in blue is the negative (west, south, and descending) component of the flow vector in Darcy velocities, calculated with ParaView's stream tracer filter for the entire model domain (Squillacote et al., 2007). In green are the mineral and thermal springs from BRGM (2016), LGB (2002), and LGRB (2006). In yellow are the artesian springs from LGRB (2015). The data on artesian conditions are only available for the eastern side of the Rhine. The white dotted line reflects the outline of the sediments of the URG.
To better assess the reliability of the simulation results we cross-plot available data on mapped springs, here used as indicators for discharge areas. Therefore, we compare the location of mineral and thermal springs (green in Fig. 5c) and artesian conditions (yellow in Fig. 5c) with the model prediction (upflows and downflows). Based on the fit between model and hydraulic data we can distinguish two main areas: (1) domains in which the model predicts uprising water where springs or artesian conditions are observed (areas 1 to 4 in Fig. 5c, f) and (2) domains in which the model only partly predicts the observed springs or artesian conditions (areas 5 to 7 in Fig. 5c, f).
Along the Western Border Fault of the URG the model can reproduce the artesian conditions (springs in area number 1 in Fig. 5c). Recharge occurs, though with moderate rates of approximately 1 × 10−8 m s−1, from the Black Forest into the crystalline crust and groundwater discharges along the Eastern Graben Fault. In the southeast of Heidelberg, the model predicts artesian conditions (area 2). Comparing the results with recently published studies (e.g., Freymark et al., 2019), we can observe a better fit with respect to the artesian conditions between Heidelberg and Karlsruhe (area 2). Our model predicts a clear upflow domain, while the model of Freymark et al. (2019) predicted recharge conditions and showed a distinct boundary effect. However, our model does not provide a good fit for the springs mapped at the Western Border Fault, which were instead reproduced by the study of Freymark and coworkers. The reason for this misfit stems from the fact that the latter model integrated the main border faults, which are structural features that have been neglected for this study. Those border faults being permeable fluid pathways resulted in improved model predictions. The impact of these features will be addressed in future studies. Despite this, focusing on area number 3 along the Eastern Border Fault of the URG, the model predicts discharge conditions and upflow of fluids, as well as at the Western Border Fault of the URG (in area number 4), which is in agreement with the data.
The misfit found for areas 5 to 7 also likely relates to uprising fluid flow, mainly fault and fracture controlled. Here we propose that a better fit could be achieved by resolving these features either as part of the mesh (discrete) or as an equivalent continuum. Likewise, the springs in area number 6 of the Black Forest are not reproduced. This is because the Black Forest acts as a recharge area in this regional-scale model, for which local-scale features are not resolved. In area 7 groundwater infiltrates from the surface following a northwest direction, parallel to the hydraulic gradients, from the northernmost area of the Black Forest into the area between Heidelberg and Karlsruhe. The observation that we cannot reproduce the artesian conditions in this area can be taken as proof that the model could not resolve some important local structural features in these domains. However, previous modeling studies (Cherubini et al., 2014; Freymark et al., 2019) have demonstrated that even large faults implemented as features that are more permeable than the geological units have only limited lateral effects on the flow field and do not change the regional, pressure-driven flow pattern. In particular, the recent modeling work of Freymark et al. (2019) deals with the influence of the border faults of the URG on the general fluid flow and heat transport. They could show that the effects of the main border faults are less important than hydraulic head and permeability contrasts between the sediments and basement. The aperture and permeability of the faults have no significant influence on the overall simulated flow and the thermal field. In order to check the plausibility of the model results concerning recharge and discharge rates, we calculated the latter for the upper model boundary. The results show that the majority of values lies in a reasonable range of ±100 mm a−1, with very few outliers showing ±1000 mm a−1, mainly related to high gradients in the Alps, a process that has been shown in previous studies (e.g., Przybycin et al., 2017). If we compare these values to the recharge data set from the hydrological atlas (BGR, 2014), we can state that the order of recharge rates fits in general. In the data set, the highest recharge rates are at the Schwarzwald, up to 500 mm a−1. With our model setup, we cannot reproduce these high recharge values because the Schwarzwald as part of the Variscan basement is parameterized with very low hydraulic conductivity, preventing high infiltration rates. There is, however, a general problem in comparing hydraulic recharge data with modeling results of the deep subsurface in that the recharge is determined without considering the subsurface deep structure. In recharge analyses soil properties are investigated down to the uppermost aquifer. In this study, we focus on the deep fluid flow and therefore neglect the unsaturated zone in the shallow subsurface. As the determination of recharge does not consider the spatial variability of flow in the deeper subsurface (which is permeability dependent), there are clear limitations related to this comparison. Further simplifications adopted for this study relate to the fluid density, which we assumed to be constant in order to focus on the regional-scale hydraulic driving mechanisms only. Here, temperature and salinity coupling poses promising targets for future studies, which has already been attempted in Freymark et al. (2019) for a subdomain of the URG and in Koltzer et al. (2019) for the northern part of the URG. The new finding of this study is that the 3-D flow field on the regional scale of the whole URG indeed has characteristics that differ from those of smaller-scale models in the domains in which the latter suffer from lateral boundary effects.
Based on the results discussed above, we end up with a revised conceptual model of the regional flow field within the URG as exemplified in Fig. 6. Higher hydraulic head gradients perpendicular to the graben than parallel to the graben axis result in a predominant flow from the graben shoulders to the center of the graben. This characteristic is applicable to the total extent of the URG and is consistent with previous studies (e.g., Freymark et al., 2019) already demonstrating that a flow regime from a recharging eastern boundary fault to a discharging western boundary fault (Clauser and Villinger, 1990) is not supported by 3-D models considering 1st-order structural characteristics. In addition, the larger spatial extent of our model compared to the model of Freymark et al. (2019) allows for the detection of additional influencing factors. Accordingly, the flow from south to north is dominant in the southern area of the graben because of the high head elevation of the Jura Mountains south of the URG. In the central part of the URG, the upflow axis shifts to the eastern area of the graben. There, the influence of the top of the Variscan basement (deepest area of the basement) plays an important role in the deep and shallow aquifer systems. In the north, the deep fluid flow is not following the surface topography northward (as the river Rhine) and the question posed at the beginning, if the deep fluid flow in the URG valley follows the topography from south to north, has to be revised. In the north of the graben, the aquitard is not fully separating the deep aquifers from the shallow aquifer, though the fluid flow is a complex result of deep and shallow hydrodynamics.
Based on the results and discussion the following major conclusions can be drawn (summarized in Fig. 6).
-
The general fluid flow direction is dependent on the hydraulic head gradients and the geometric configuration of the permeable units. The high hydraulic gradients at the graben shoulders and low gradients in the Rhine Valley in concert with the northward-inclined base of the Cenozoic sediment fill cause a flow direction perpendicular to the flow direction of the river Rhine and perpendicular to the graben axis, from the graben shoulders towards its center.
-
Local flow heterogeneities in the graben can be structurally linked to the topology of the top basement configuration of the Variscan basement.
-
Two separated flow systems evolve in the Upper Rhine Graben that show different degrees of decoupling through the local presence or absence of the Keuper aquitard.
Ongoing activities focus on potential modifications of the flow field if full thermo-hydraulic coupling is considered and on the role of the tectonic structures on the regional flow component, which might be overprinted locally as identified by the clustering of localized hydrothermal surface manifestations (springs as per Fig. 5c).
The data used to support the findings of this study are available from the corresponding author upon request.
NK and JB prepared the concept for this study. NK and MF built the model. NK prepared the paper with contributions from all coauthors. MS-W, JB, and MC supervised this work.
The authors declare that they have no conflict of interest.
This article is part of the special issue “European Geosciences Union General Assembly 2019, EGU Division Energy, Resources & Environment (ERE)”. It is a result of the EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019.
We are grateful to the Federal Ministry for Economic Affairs and Industry for funding this research (grant number: 0325944B). Moreover, we are thankful for the cooperation with the Technical University of Darmstadt within the project Hessen 3D 2.0 and to HLNUG for providing hydrological data. For the sponsored MIKE Powered by DHI license files, we kindly acknowledge DHI WASY. We want to thank the anonymous reviewers for their contributions, which helped improve the quality of this paper.
The article processing charges for this open-access publication were covered by a Research Centre of the Helmholtz Association.
This paper was edited by Michael Kühn and reviewed by two anonymous referees.
Bär, K.: Untersuchung der tiefengeothermischen Potenziale von Hessen, TU Darmstadt, 297 pp., 2012.
BGR: Geologische Karte der Bundesrepublik Deutschland 1 : 1 000 000 (GK1000), Bundesanstalt für Geowissenschaften und Rohstoffe, 2014.
BRGM: Hydraulic heads Median 2000–2016: http://www.ades.eaufrance.fr/, last access: 16 June 2016.
Cherubini, Y., Cacace, M., Scheck-Wenderoth, M., and Noack, V.: Influence of major fault zones on 3-D coupled fluid and heat transport for the Brandenburg region (NE German Basin), Geoth. Energ. Sci., 2, 1-20, https://doi.org/10.5194/gtes-2-1-2014, 2014.
Clauser, C. and Villinger, H.: Analysis of conductive and convective heat transfer in a sedimentary basin, demonstrated for the Rheingraben, Geophys. J. Int., 100, 393–414, 10.1111/j.1365-246X.1990.tb00693.x, 1990.
Dèzes, P., Schmid, S. M., and Ziegler, P. A.: Evolution of the European Cenozoic Rift System: interaction of the Alpine and Pyrenean orogens with their foreland lithosphere, Tectonophysics, 389, 1–33, 10.1016/j.tecto.2004.06.011, 2004.
Diersch, H.-J.: FEFLOW – Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media, 1st edn., Springer-Verlag Berlin Heidelberg, Heidelberg, 2014.
Freymark, J., Sippel, J., Scheck-Wenderoth, M., Bär, K., Stiller, M., Kracht, M., and Fritsche, J.-G.: Heterogeneous Crystalline Crust Controls the Shallow Thermal Field – A Case Study of Hessen (Germany), Energ. Proc., 76, 331–340, https://doi.org/10.1016/j.egypro.2015.07.837, 2015.
Freymark, J., Sippel, J., Scheck-Wenderoth, M., Bär, K., Stiller, M., Fritsche, J.-G., and Kracht, M.: The deep thermal field of the Upper Rhine Graben, Tectonophysics, 694, 114–129, https://doi.org/10.1016/j.tecto.2016.11.013, 2017.
Freymark, J., Bott, J., Cacace, M., Ziegler, M., and Scheck-Wenderoth, M.: Influence of the Main Border Faults on the 3D Hydraulic Field of the Central Upper Rhine Graben, Geofluids, 2019, 7520714, https://doi.org/10.1155/2019/7520714, 2019.
Frick, M., Sippel, J., Cacace, M., and Scheck-Wenderoth, M.: The geothermal field below the city of Berlin, Germany, results from structurally and parametrically improved 3-D models, Energ. Proc., 97, 334–341, https://doi.org/10.1016/j.egypro.2016.10.011, 2016.
GeORG-Projektteam: Geopotenziale des tieferen Untergrundes im Oberrheingraben, Fachlich-Technischer Abschlussbericht des INTERREG-Projekts GeORG, Teil 1: Ziele und Ergebnisse des Projekts, Freiburg i. Br., 103 pp., 2013a.
GeORG-Projektteam: Geopotenziale des tieferen Untergrundes im Oberrheingraben, Fachlich-Technischer Abschlussbericht des INTERREG-Projekts GeORG, Teil 2: Geologische Ergebnisse und Nutzungsmöglichkeiten, Freiburg i. Br., 346 pp., 2013b.
GeORG-Projektteam: Geopotenziale des tieferen Untergrundes im Oberrheingraben, Fachlich-Technischer Abschlussbericht des INTERREG-Projekts GeORG, Teil 3: Daten, Methodik, Darstellungsweise, Freiburg i. Br., 242 pp., 2013c.
Guillou-Frottier, L., Carrė, C., Bourgine, B., Bouchot, V., and Genter, A.: Structure of hydrothermal convection in the Upper Rhine Graben as inferred from corrected temperature data and basin-scale numerical models, J. Volcanol. Geoth. Res., 256, 29–49, 10.1016/j.jvolgeores.2013.02.008, 2013.
Herrmann, F.: Entwicklung einer Methodik zur großräumigen Modellierung von Grundwasserdruckflächen am Beispiel der Grundwasserleiter des Bundeslandes Hessen, Fakultät für Umweltwissenschaften und Verfahrenstechnik Brandenburgische technische Universität Cottbus, 2010.
Jodocy, M. and Stober, I.: Porositäten und Permeabilitäten im Oberrheingraben und Südwestdeutschen Molassebecken, Erdöl Kohle Erdgas, 127, 20–27, 2011.
Koltzer, N., Scheck-Wenderoth, M., Bott, J., Cacace, M., Frick, M., Sass, I., Fritsche, J.-G., and Bär, K.: The Effects of Regional Fluid Flow on Deep Temperatures (Hesse, Germany), Energies, 12, 2081, https://doi.org/10.3390/en12112081, 2019.
Lampe, C. and Person, M.: Advective cooling within sedimentary rift basins – application to the Upper Rhinegraben (Germany), Mar. Petroleum Geol., 19, 361–375, https://doi.org/10.1016/S0264-8172(02)00022-3, 2002.
LFU: Helvetikum- und Flyschzone, Hydrogeologischer Teilraum, Bayerisches Landesamt für Umwelt, https://www.lfu.bayern.de/geologie/hydrogeologie_karten_daten/hydrogeologische_raumgliederung/teilraum/doc/teilraum_helvetikum_flyschzone.pdf (last access: 21 May 2019), 2007.
LGB: Karte der Mineral-, Heil, und Thermalwässer von Rheinland-Pfalz, Landesamt für Geologie und Bergbau Rheinland-Pfalz, Wiesbaden, available at: https://www.lgb-rlp.de/de/karten-und-produkte/online-karten/online-karte-mineralwasser.html (last access: 21 May 2019), 2002.
LGRB: LGRB-BW HÜK350: Mineral-/ Thermalwässer, Landesamt für Geologie, Rohstoffe und Bergbau, Wiesbaden, 2006.
LGRB: LGRB-BW ISONG: Artesische Grundwasserverhältnisse, Landesamt für Geologie, Rohstoffe und Bergbau, Wiesbaden, 2015.
LUBW: Hydraulic head Mean 1980–2016, Landesanstalt für Umwelt, Baden-Württemberg, 2016a.
LUBW: Hydraulic head Mean 1986–2016, Landesanstalt für Umwelt, Baden-Württemberg, 2016b.
Noack, V., Scheck-Wenderoth, M., Cacace, M., and Schneider, M.: Influence of fluid flow on the regional thermal field: results from 3D numerical modelling for the area of Brandenburg (North German Basin), Environ. Earth Sci., 70, 3523–3544, 2013.
Pribnow, D. and Clauser, C.: Heat and fluid flow at the Soultz hot dry rock system in the Rhine Graben, in: Proceedings World Geothermal Congress, World Geothermal Congress, Kyushu-Tohoku, Japan, 28 May–10 June, 2000.
Przybycin, A., Scheck-Wenderoth, M., and Schneider, M.: The origin of deep geothermal anomalies in the German Molasse Basin: results from 3D numerical models of coupled fluid flow and heat transport, Geotherm. Energy, 5, 27, https://doi.org/10.1186/s40517-016-0059-3, 2017.
Squillacote, A. H., Ahrens, J., Law, C., Geveci, B., Moreland, K., and King, B.: The paraview guide, Kitware Clifton Park, NY, 2007.
Stober, I. and Bucher, K.: Hydraulic conductivity of fractured upper crust: insights from hydraulic tests in boreholes and fluid-rock interaction in crystalline basement rocks, Geofluids, 15, 161–178, https://doi.org/10.1111/gfl.12104, 2015.
Stober, I. and Jodocy, M.: Eigenschaften geothermischer Nutzhorizonte im baden-württembergischen und französischen Teil des Oberrheingrabens, Grundwasser, 14, 127–137, https://doi.org/10.1007/s00767-009-0103-3, 2009.