Sensitivity analysis of gas leakage through a fault zone during subsurface gas storage in porous formations

Subsurface gas storage in porous media is a viable option to mitigate shortages in energy supply in systems largely based on renewable sources. Fault systems adjacent to or intersecting with gas storage could potentially result in a leakage of stored gas. Variations in formation pressure during a storage operation can affect the gas leakage rates, requiring a site and scenario specific assessment. In this study, a geological model of an existing structure in the North German Basin (NGB) is developed, parameterised and a methane gas storage operation is simulated. Based on the observed storage pressure, a sensitivity study aimed at determining gas leakage rates for different parametrisations of the fault damage zone is performed using a simplified 2-D model. The leakage scenario simulations show a strong parameter dependence with the fault acting as either a barrier or a conduit for gas flow. Furthermore, the storage operation greatly affects the gas leakage rates for a given parametrisation with significant leakage only during the injection periods and thus during increased overpressures in the storage formation. During injection, the peak leakage rates can be as high as 2308 Sm³ d⁻¹ for damage zone permeabilities of 10 mD and a capillary entry pressure of 4 bar. Increasing capillary entry pressure results in a sealing effect. If the capillary entry pressure is scaled according to the damage zone permeability, peak leakage rates can be higher, i.e. 3240 Sm³ d⁻¹ for 10 mD and 0.13 bar. During withdrawal periods, the pressure gradient between a storage formation and a fault zone is reduced or even reversed, resulting in greatly reduced leakage rates or even a temporary stop of the leakage. Total leakage volume from storage formation was assessed based on the 2-D study by considering the exposure of the gas-filled part of the storage formation to the fault zone and subsequently compared with gas in place volume.

1 Introduction

Worldwide, countries are promoting a transition from conventional to renewable energy sources to mitigate global climate change (IPCC, 2015). In Germany, the so-called “Energiewende” resulted in 31.6 % of the total power generation in the year 2016 being based on renewable sources, with the overall aim being 80 % by the year 2050 (BMWi, 2018). However, power generation from renewable sources is stochastic, so that the fluctuating availability of wind and solar radiation can cause challenges for an optimal management of energy system and energy storage on various scales might be required in systems largely based on renewable power generation (Schiebahn et al., 2015). The geological subsurface and specifically porous formations can provide large storage capacities for gases (Bauer et al., 2013; Kabuth et al., 2017), either for a mechanical energy storage concept utilising compressed air (Wang and Bauer, 2017; Mouli-Castillo et al., 2019; Sopher et al., 2019) or for storing a chemical energy carrier, such as hydrogen or methane (Sainz-Garcia et al., 2017; Pfeiffer et al., 2017; Matos et al., 2019).

The North German Basin has previously been investigated for CO₂ storage (e.g. Schäfer et al., 2010; Kempka et al., 2015). This led to the identification of several potential storage sites (Hese, 2012), which used for storing other gases such as methane or compressed air. However, fault systems exist throughout the NGB, including the identified storage sites, which introduces uncertainty regarding the possibility of gas leakage (Oldenburg et al., 2002; Folga et al., 2016). Such a leakage of gas would not only result in a reduced gas in place (GIP), but also in a potential drop in formation pressure, both resulting in a reduced storage capacity and storage self-discharging over time. Furthermore, gas leaking from a subsurface storage site into shallow formations can trigger chemical reactions and can have an adverse effect on e.g. drinking water supplies (Kempka et al., 2015). Consequently, an assessment of potential gas leakage rates is useful to be able to assess potential impacts prior to any storage development or operation.

The leakage of gas from a gas storage site is driven by the buoyancy of the lighter gas compared to the surrounding formation water as well as the pressure gradient between the storage formation and the fault zone (Chen et al., 2013). During a gas storage operation, the storage pressure fluctuates several bars, depending on the current operational mode and storage setup, e.g. up to ±35 bar for a hydrogen storage site designed for weekly withdrawal periods (Pfeiffer et al., 2017) and ±41.5 bar for a compressed air energy storage used in a daily storage scheme (Wang and Bauer, 2017). Studies on gas leakage during natural gas storage show that frequent pressure fluctuations in the storage formation can affect leakage rates through fault zones intersecting the gas storage site (Chen et al., 2013). In addition to the changes in formation pressure due to the storage operation, also the properties of the fault system and its internal structure affect leakage of fluids. However, such fault zone properties are often unknown and are subject to uncertainties (Gibson, 1998; Fisher and Knipe, 2001; Faulkner et al., 2003). The effect of existing fault systems on the operation at a potential storage site, i.e. occurring leakage rates and resulting reduction in formation pressure, must be investigated prior to any deployment. This study is aimed at investigating leakage characteristics during a storage operation at a potential gas storage site in the NGB for different fault zone parametrisations. For this, first a geological model of a potential gas storage site in the NGB, which includes six individual faults, was constructed. A hypothetical methane storage operation is designed and the storage operation is simulated using a 3-D reservoir model to obtain realistic storage pressures. Subsequently, a sensitivity analysis aimed at determining leakage rates for different fault zone parametrisations is carried out on a 2-D slice of the model area.

2 Geological storage model

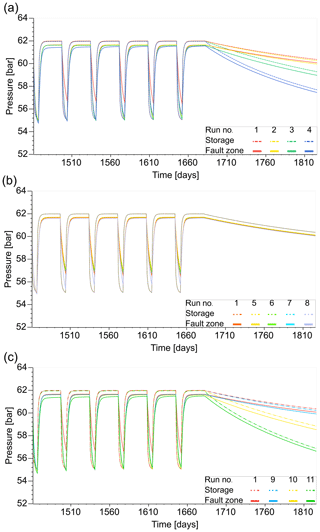
A potential gas storage site must satisfy the following criteria: a sufficiently high reservoir volume to store the desired amount of gas, a high intrinsic permeability to provide the required flow rates and a satisfactory containment of the stored gas (e.g. Bennion et al., 2000; Matos et al., 2019). In the NGB the Quickborn-Volpriehausen, the Rhaetian and the Dogger sandstones are potential storage formations, as they typically provide sufficiently high permeabilities and occur in combination with potential cap rocks (Hese, 2012). Due to salt tectonics within the NGB, all sedimentary depositions were affected by changes in regional stresses (Baldschuhn et al., 2001; Hese, 2012). This resulted in formation of potentially suitable geological traps as well as major fault systems (Baldschuhn et al., 2001; Lehné and Sirocko, 2005). These major fault systems typically strike N–S to NNE–SSW (Fig. 1a). Local faults striking in different directions often accompany the major fault systems on the top and sides of salt structures (Baldschuhn et al., 2001; Reinhold et al., 2008). The combination of the number of fault systems and the different strike directions results in a complex sedimentary architecture in the NGB. Structural model used for the investigation of gas leakage from a storage site must represent this complexity and should therefore include all existing structures.

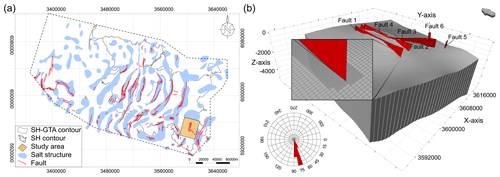
Figure 1 (a) Salt structures, associated faults and the study area within the NGB in Schleswig-Holstein (SH). The dashed outline is the area of Geotectonic Atlas of Northwestern Germany and the German North Sea (GTA) within SH (after Baldschuhn et al., 2001; Hese, 2012); (b) 3-D geological structure model created for the study with six fault systems (average dip angle 61 to 82^∘).

In this study, a structural model of a potential storage structure was previously investigated for CO₂ (Hese, 2012) and later for hydrogen storage (Pfeiffer et al., 2017) and is created and used for the scenario simulations. At the storage site, an anticline trap was formed by halokinesis, with normal and reverse faults intersecting with the structure and providing potential leakage pathways for fluid migration (Fig. 1b). In the previous study by Pfeiffer et al. (2017), the faults at the study site are assumed to be sealing and boundary conditions were chosen accordingly for the flow simulation model. Of the three potential storage formations in the NGB, only the Quickborn-Volpriehausen and the Rhaetian sandstones exist at the storage site. While the Quickborn-Volpriehausen sandstones are at depths of 1860 unitm, the Rhaetian sandstones are located at a more suitable, shallower depth of around 400 m. In total, 14 deep (Permian till Paleogene) and 9 shallow (Miocene till Pleistocene) base horizons were used to create the 3-D geological model, which has a spatial extend 23.5 km by 27.7 km by 6 km. The modelling was done using the Petrel E&P platform, based on horizon and fault data provided and calibrated based on six well drilling data and seven seismic profiles by Hese (2012). For each fault system, the geometrical fault-fault and fault-horizon interrelationships are considered. The fault systems are featured in a discrete corner point grid, which enables the representation of the fault zone complexity and allows local grid refinements, according to the requirements of the study (Fig. 1b). The structural analysis of fault systems at the study site shows a dip-slip movement tendency. The average dip angle of Faults 1, 3 and 4 is 70^∘. Fault 2 has a lower average dip angle of 61^∘, while Faults 5 and 6 show a higher average dip angle of 82^∘. The primary strike direction is NE–SW, similar to the major salt structures in the NGB (Reinhold et al., 2008). The fault systems crosscut the Triassic storage formations and reach up to the Oligocene horizon (Baldschuhn et al., 2001). The average fault throw is 30 m with a total displacement of 35 m. However, locally the fault throw can reach 200 m and total displacement can be up to 240 m, which can serve as a rough probability indicator for faults acting as a possible leakage pathway (Knipe et al., 1997; Manzocchi et al., 1999; Shipton and Cowie, 2001).

During the formation of such faults, the grains of the host rock are crushed and re-arranged along the deformation band, resulting in the formation of breccias, catalaclasites, ultracataclasites and veins (Aydin, 1978; Caine et al., 1996). The adjacent rock matrix to each side of the deformation band is typically densely fractured (Caine et al., 1996; Fossen et al., 2007). The petrophysical properties of these two zones differ significantly, which is commonly represented by distinguishing between a fault core and a damage zone (Aydin, 1978; Caine et al., 1996; Faulkner et al., 2003). Understanding the fluid flow processes occurring in a fault zone requires the investigation of the main characteristics of the system, i.e. the fault core, the damage zones and the adjacent host rock. The properties of these units affecting fluid flow are hydraulic permeability and capillary entry pressure as well as spatial extent (Knipe et al., 1997).

Due to the aforementioned processes, the fault core typically acts as a barrier towards fluid flow, i.e. the permeability is lower than that of the undisturbed host rock (Aydin, 1978; Caine et al., 1996; Gibson, 1998). The petrophysical properties within a fault zone formed through a deformation band mechanism are controlled by the host rock properties and permeability reductions of approximately 4 to 6 orders of magnitude compared to the original host rock can be observed (Knipe et al., 1997; Gibson, 1998; Faulkner et al., 2003). Studies show that the fault core permeability is within the range from 10⁻² to 10⁻⁶ mD for siliciclastic rocks similar to those found in the NGB (Caine et al., 1996; Gibson, 1998; Shipton and Cowie, 2001; Faulkner et al., 2003; Flodin et al., 2005). The damage zones are the area or volume of host rock affected by the fault genesis to both sides of the fault core (Aydin, 1978; Caine et al., 1996; Faulkner et al., 2003). Contrary to the fault core, damage zones typically have hydraulic conductivities that are higher than the respective host rock due to high density of fractures, faults and cleavage (Caine et al., 1996). For siliciclastic rocks, damage zone permeabilities typically range from 10 to 10⁻² mD (Gibson, 1998; Torabi et al., 2013; Rinaldi et al., 2014b). Capillary processes can be significant due to the reservoir rock being juxtaposed across the fault zone against the upper formations. Capillary entry pressure is one of the important parameters controlling the fluid flow in such conditions, with values given in literature typically ranging from 4 to 100 bar (Knipe et al., 1997; Gibson, 1998; Flodin et al., 2005; Torabi et al., 2013). Experimental and literature studies have shown that damage zones can reach up to 100 m on both sides from fault centre, whereas fault cores have significantly smaller thicknesses of less than 0.5 m (Knipe et al., 1997; Shipton and Cowie, 2001; Faulkner et al., 2003).

3 Gas storage simulation

The pressure fluctuations induced by a storage operation depend on the thickness and extent of the storage formation, the petrophysical properties of the storage formation as well as the injection/withdrawal history and the underlying storage scenario, which dictates the boundary conditions for the storage operation. For this study, a storage scenario is constructed, based on the assumption periods with no power generation from renewable sources for one week. In 2016 the average weekly electricity demand of the state of Schleswig-Holstein was about 1.04 million GJ (MELUR, 2018). Taking this as a reference and assuming the efficiency of re-electrification of methane to be 60 % (Schiebahn et al., 2015), a storage site must provide 48.4 million Sm³ (at surface conditions) of synthetic natural gas during the period of 7 d to cover the complete storage demand of such scenario.

The storage operation consists of an initial filling of the storage with gas, a cycling storage operation and a subsequent shut-in period. The initial gas injection lasts for 1460 d, during which 263 million Sm³ of gas are injected. The cyclic operation consists of six storage cycles, with the withdrawal rate in each cycle being set to 1.4 million Sm³ d⁻¹ per well. Each withdrawal period is followed by refilling of the storage formation with gas at a rate of 350 000 Sm³ d⁻¹ per well for 30 d. Subsequent to the cyclic operation, a shut-in period of 222 d is simulated, resembling a temporary abandonment of the operation.

Figure 2 Gas phase distribution in the 3-D model after the storage initialisation. Five vertical storage wells located near the top of the anticline, 900 m from well 1 is the “virtual” well for pressure controlling in 2-D study.

The storage operation is simulated using five vertical wells located near the top of the anticline at the depths of 429, 458, 484, 514 and 554 m (Fig. 2). The corresponding initial well pressures are 43.0, 46.0, 48.6, 51.6 and 55.4 bar. The gradient of the minimum horizontal stress of the suprasalinar sediments in the NGB is estimated to be around 0.15 bar m⁻¹ (Röckel and Lempp, 2003). Assuming this to be the fracture pressure gradient and thus the maximum allowable pressure increase, the upper bottom hole pressure (BHP) values in wells 1 to 5 are calculated as 64.3, 68.7, 72.6, 77.1 and 83.1 bar, respectively. The lower pressure limit of the wells during withdrawal were set to an arbitrary 30 bar. Geomechanical processes such as fault reactivation are not explicitly considered in this study. However, with the defined BHP limits geomechanical reactions due to the storage operation are assumed unlikely. To minimise the computational load, the Rhaetian storage formation and the cap rocks are included in this simulation, with the spatial discretisation 50 m by 50 m in lateral directions. At the storage site, the mudstones of the Lias and the Lower Cretaceous form the cap rocks above the storage formation. However, the Lias is eroded towards the fault axis, so that only the Lower Cretaceous forms a complete seal over the storage formation.

The model is discretised in vertical direction by dividing the individual units, i.e. the cap rocks and the storage formation, into a constant number of layers. The resulting vertical discretisation of the grid varies therefore with the local thickness of the individual unit. The storage formation is divided into five layers, with the resulting vertical discretisation ranging from 0.01 to 26 m. The Lias and the Lower Cretaceous cap rocks are discretised using twenty layers, with resulting vertical discretisation ranging from 0.001 to 13 m and 1 to 5 m, respectively. No flow is allowed across the model boundaries, providing a conservative estimation of the pressure changes occurring during the storage operation, as overpressures cannot dissipate. All petrophysical properties are assumed as homogeneous and isotropic within the individual geological units (Table 1). The Brooks and Corey formulation (Brooks and Corey, 1946) is used to calculate phase permeabilities and capillary pressure, based on phase saturations. The ECLIPSE E100 black-oil simulator is used (Schlumberger Ltd., 2017), assuming immiscible two-phase flow of water and gas. It was successfully tested in a benchmark paper by Class et al. (2009) for a comparable setting and represents therefore a valid choice as modelling tool.

Table 1 Model parameters used for 3-D gas storage simulation.

During initial storage filling, the injected gas accumulates at the top of the anticline (Fig. 2). The initial filling of the storage is accompanied with a significant pressure increase, so that the BHP in well 1 reaches the upper limit after 300 d, resulting in an automatic reduction of applied injection rates and ultimately in the well being shut after 1410 d (Fig. 3). For the deeper wells 2, 3, 4 and 5 the upper limit is not exceeded during the initial filling, with well pressures peaking at 65.9, 67.0, 67.6 and 68.3 bar, respectively.

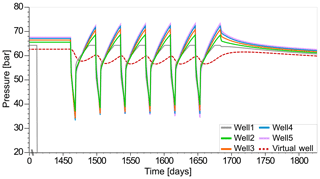
Figure 3 Bottom hole pressure for five vertical wells during the storage cyclic operation starting at day 1461 and the following shut-in period of 222 d; the dashed red line depicts the pressure change at the position of the 2-D-slice used for the leakage scenario simulations.

The target withdrawal rates of 1.4 million Sm³ d⁻¹ are sustained for all wells in all storage cycles, so that 49 million Sm³ of gas is produced from the storage formation in each cycle. During the first storage cycle the well pressures decrease to 38.5, 37.1, 34.2, 33.3 and 34.1 bar in wells 1 to 5, respectively. In the subsequent refilling period, the target injection rates are achieved in wells 2 to 5, while the upper BHP limit is reached in well 1. Thus, less gas can be injected than planned, with the total injected gas volume being 50.9 million Sm³. Regardless, the target withdrawal rates are achieved in every storage cycle, so that the storage site can cover 100 % of the storage demand, as defined in this study. The storage pressure follows the trend of well pressure with the magnitude of the pressure change during different storage phases being considerably dampened (Fig. 3). After the initial filling, the storage pressure 900 m south of the storage wells, which is the position of the 2-D slice used for the leakage scenario simulations, is around 62 bar. During the storage operation, pressure fluctuates between about 60 and 55 bar. Thus, the observed pressure changes during the storage operation is 7 bar at the position of the 2-D model. In the shut-in period of the storage operation after 1683 d, the storage pressure rebounds to 62.0 bar and then slowly declines to around 59.9 bar at the end of simulation at the day 1827.

4 Gas leakage simulations

4.1 Setup

For the leakage simulations, only a 2-D slice extracted from the full 3-D model is used (Fig. 2), with the initial and boundary conditions being set based on the simulation results of the full 3-D model of the storage operation. The 2-D slice is oriented W–E, intersecting with the gas storage at about 900 m south of the storage well 1. The slice position was selected to represent realistic storage pressures, a high local gas volume, as well as a good approximation of the fault-storage interface (Fig. 2). At the given slice position, the pressure in the storage formation fluctuates during the cyclic storage operation by 7 bars, as can be seen from the 3-D simulation (Fig. 3). For a realistic representation of storage pressure, an additional well is placed 350 m east from the fault zone in the 2-D model that does not exist in the 3-D model. The operation of this “virtual” well is the pressure control, i.e. the temporal evolution of storage pressure in the 3-D model is represented by cycling the pressure at the virtual well between the minimum pressure of 55 bar and the maximum pressure of 62 bar observed in the 3-D model (Fig. 3). The petrophysical properties of the fault damage zone are directly assigned to the grid elements. Using local grid refinement, the first 50 m from the fault zone and the storage formation were refined to grid blocks of 50 m by 1 m in lateral direction. The fault core properties are assigned using transmissibility multipliers at the connecting grid blocks (Manzocchi et al., 1999). For the leakage scenario simulations, only the cyclic storage phase and the subsequent shut-in period are considered. Thus, the initial formation pressure is assumed to be 62.7 bar (compare Fig. 3).

Table 2 Model parameters used for leakage scenario simulations.

Three different scenario parametrisations are tested in this study (Table 2). In the scenario I only the permeability of the damage zone is changed, while in the scenario II the capillary entry pressures are being varied. In the scenario III, both the damage zone permeability and the capillary entry pressure are varied simultaneously based on the Leverett J-function scaling (Leverett, 1941). For this, 0.01 mD and 4 bar are set as the respective reference permeability and capillary entry pressure. Thus, increasing damage zone permeabilities are accompanied by decreasing capillary entry pressures in the simulation runs of the scenario III.

Figure 4 Pressure fluctuation during cycling operation in 2-D model, solid lines represent pressure in the fault zones: (a) scenario I – for the damage zone permeability cases; (b) scenario II – for capillary entry pressure cases; (c) scenario III – for normalised capillary entry pressure cases.

4.2 Simulation results and discussion

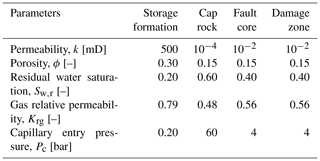
The leakage simulations start with a withdrawal cycle, during which the pressure in the storage formation decreases to values close to 55 bar and the fault zone pressures being 55.0, 55.0, 54.9 and 54.8 bar for simulation runs #1 to #4 (Fig. 4a). Even though the pressure differential between the storage formation and the fault zone is small, the gas leaks into the fault zone and rises upwards (Fig. 5). The peak gas leakage rates are 325 and 2308 Sm³ d⁻¹ in simulation runs #3 and #4, while runs #1 and #2 show leakage rates below 25 Sm³ d⁻¹.

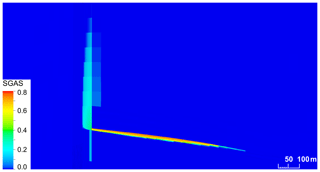
Figure 5 Exemplary gas phase saturation in the fault zone at day 1827 in run #11, scaled-up by 3 units in z axis. Gas flows from the storage formation to the damage zone is directed upwards within the damage zone.

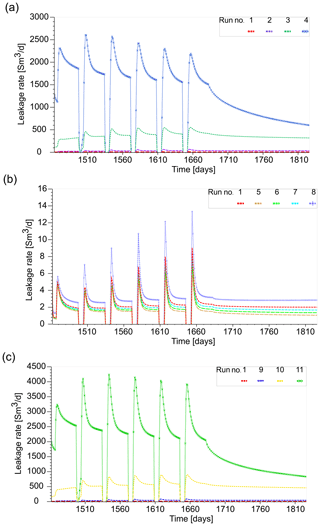
Figure 6 Gas leakage rates during six injection periods for: (a) scenario I – damage zone permeability cases; (b) scenario II – capillary entry pressure cases; (c) scenario III – normalised capillary entry pressure cases.

During the subsequent injection period from day 1468 to day 1498, the pressure in the storage formation rapidly increases, with the fault zone pressure following behind (Fig. 4a). Correspondingly, gas leakage occurs with peak rates being 5, 24, 325 and 2308 Sm³ d⁻¹ during the first injection for the simulation runs #1 to #4 of the scenario I (Fig. 6a). However, the rates quickly decline within the first hours of injection for the simulation case, assuming a damage zone permeability of 10 mD (run #4) with the average leakage rate being 2020 Sm³ d⁻¹. Contrary to that, the peak and average leakage rates are relatively constant in the remaining simulation runs. During the following withdrawal of gas, the pressure in the storage formation is again dropping to around 55 bar, which greatly reduces the gas leakage for the higher permeability simulation runs (#3, #4) and stops it for in the lower permeability runs (#1, #2) altogether (Fig. 4a). The characteristics of the gas leakage rates are similar in the subsequent storage cycles, however, the differences between the peak and average leakage rates during injection increase slightly. In the dormant phase of the storage operation after 222 d of operation, gas leakage rates gradually decrease to around 2, 35, 348 and 866 Sm³ d⁻¹ for damage zone permeabilities of 0.01, 0.1, 1 and 10 mD, respectively. This happens while the pressure differential between the storage formation and the fault zone remains relatively constant (Fig. 4a).

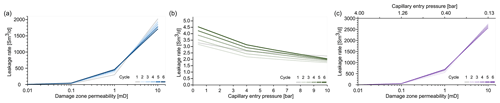
Figure 7 Comparison of the influence of fault zone parameters on the average leakage rate during six injection periods; Parameters: (a) damage zone permeability; (b) capillary entry pressure; (c) scaled capillary pressure and damage zone permeability.

For the different capillary entry pressure cases at a constant fault zone permeability of 0.01 mD (scenario II), the gas leakage rate never exceeds 15 Sm³ d⁻¹ during injection (Fig. 6b). For the simulation cases with higher capillary entry pressures, i.e. 6, 8 and 10 bar, the differential between the gas phase pressure in the storage and the fluid pressure in fault system is not sufficient to result in significant leakage. For the simulation case with the lower capillary entry pressure (run #8), the highest leakage rates of the scenario II are observed. However, the low damage zone permeability retards the advance of the gas phase sufficiently to minimise gas leakage. The low pressure differential between the storage formation and the fault zone inhibits any leakage during the first withdrawal period in simulation runs #1, #5 to #8. The pressure in the fault zone is not lower than the storage formation pressure in the following withdrawal cycles, so that no gas leakage occurs (Fig. 4b). In the shut-in period of the storage operation, the gas leakage rates are constant, never exceeding 3.5 Sm³ d⁻¹.

The overall characteristics of the gas leakage in the scenario III, i.e. when capillary entry pressure is scaled according to the permeability of the damage zone (runs #9 to #11), are similar to the results of the scenario I (Fig. 4a, c). However, the gas leakage rates are generally higher than in the scenario I, with peak leakage rates being 30, 473 and 3240 Sm³ d⁻¹, in simulation runs #9, #10 and #11, respectively (Fig. 6c). For the simulation runs with higher fault zone permeabilities, a decrease in the leakage rates is observed, so that in simulation run #11 (10 mD, 0.13 bar) the average gas leakage rate is 2770 Sm³ d⁻¹. For the low permeability case, the peak and average leakage rates only show a small decrease over the injection periods. In the shut-in phase of the storage operation, leakage rates gradually decrease to around 47, 497 and 1143 Sm³ d⁻¹, for damage zone permeabilities of 0.1, 1 and 10 mD, in combination with scaled entry pressures of 1.26, 0.4 and 0.13 bar, correspondingly.

For all tested scenarios, an increase in the peak gas leakage rate is observed with the number of storage cycles (Fig. 6). This can be explained by changes in the phase mobility over time. After the first couple of storage cycles, gas intrudes into the fault zone (Fig. 5), resulting in a reduced water saturation. Correspondingly, the relative permeability of gas in the affected area increases, while the relative permeability of water decreases. This increased gas mobility results in a further advance of the gas intrusion as the buoyancy of the gas drives it upwards. During the withdrawal cycles with no or only very little gas entering the fault zone, so this can result in decreasing gas saturations and thus a reduced mobility. After all storage cycles are completed, i.e. in the dormant phase of the storage, leakage rates decrease for all scenarios asymptotically, as the overpressures in the storage formation are redistributed and local pressure gradients decrease.

Comparing the average leakage rates during the injection phases of the storage operation shows a strong dependence of the observed leakage rates on the damage zone permeability and the capillary pressure (Fig. 7). Unsurprisingly, leakage rates decrease with increasing capillary entry pressure and decreasing damage zone permeability. Considerable gas leakage occurs when the damage zone permeability is greater than 1 mD. The capillary entry pressure acts as the main sealing mechanism with no significant gas leakage in any of the tested cases (Fig. 7b). However, the capillary entry pressure strongly depends on geometry of the pores within the rock formation, as does the permeability. Considering this, by scaling the capillary entry pressure according to the damage zone permeability shows a significant increase in the gas leakage rates for higher permeabilities and thus lower capillary entry pressures (Fig. 7c).

Based on the leakage rate observed in the 2-D model, the total leakage rate and the leakage volume can be calculated by considering the exposure of the gas-filled part of the storage formation to the fault zone. For the given site, the total exposure length is about 3900 m (Fig. 3). Thus, the total leakage rate is in the range from 1.3×10² to 2.2×10⁵ Sm³ d⁻¹ during the injection periods of the storage operation and 0.2×10² to 1.5×10⁵ Sm³ d⁻¹ during withdrawal. During a complete storage cycle the total gas leakage volume is in the range from 4.3×10³ to 7.5×10⁶ Sm³, corresponding to 0.002 % to 2.8 % of the total GIP.

5 Summary and conclusion

In this study, the leakage of gas along a fault system during a subsurface gas storage operation at an existing geological structure was investigated and the dependence of the gas leakage rates on the fault damage zone permeability and capillary entry pressure was analysed. A 3-D structural-geological model of the hypothetical storage site was constructed and used to simulate a storage operation to obtain realistic boundary conditions for the sensitivity analysis. The storage operation was designed to provide enough electricity for one week to offset a complete lack of renewable power generation in the state of Schleswig-Holstein, home to around 2.8 million people. With the baseline characterisation, the gas storage can deliver 100 % of the target power demand over a period of 7 d using five vertical wells. At the storage-fault interface this storage operation results in pressure changes between injection and withdrawal of around 7 bar. The leakage scenario simulations show that the fault zone intersecting the storage formation can act as either a conduit or a barrier for fluid flow, depending on petrophysical parameters, the fluid flow properties and the current storage operation. During gas injection the storage pressure increases, thus the peak leakage rates are observed during these phases with values as high as 3000 Sm³ d⁻¹ for damage zone permeabilities of 10 mD and capillary entry pressures of 0.13 bar. For lower damage zone permeabilities and higher capillary entry pressures, the gas leakage during injection is greatly reduced. However, the reduced or even reversed pressure differential between the storage formation and the fault zone during withdrawal periods can stop the leakage of gas altogether regardless of the parametrisation of the fault zone. Thus, for storage demand cases with long injection and short withdrawal periods gas leakage might be more prominent than in cases with equal length withdrawal and injection periods. The simulations show that the total leakage volume within one cycle is less than 1.0 % of the GIP in the storage formation in most cases. For a highly permeable damage zones, the simulated leakage volume can reach up to 2.8 % of the total GIP.

The presented study considers isotropic and homogeneous petrophysical properties in each individual (geological) unit. In reality, however, all formations and fault zones show spatial heterogeneity in their petrophysical parameters. A heterogeneous permeability distribution in the storage formation could result in a local increase or decrease of the formation pressure, compared to the homogenous case (Pfeiffer et al., 2017). As shown in this and the previous studies such pressure changes affect the leakage rates occurring in the fault zone. Furthermore, heterogeneity in the fault zone can cause an appearance of impermeable lenses (Fredman et al., 2007; Torabi et al., 2013), resulting in a decrease in gas leakage rate and thus total leakage volume. It can also be expected that heterogeneity in the fault zone can prevent significant flow upwards within the damage zone, while the increase in pore pressure and the resulting reduction in effective normal stress on the fault core can lead to its reactivation, potentially increasing the fault core permeability (Rinaldi et al., 2014a). To consider these processes in fully coupled hydro-mechanical process simulations a detailed analysis and characterisation of the (site-specific) mechanical properties of a fault zone is required.