Assessing future ice-sheet variability for long-term safety of deep geological repositories

In many regions considered for deep geological repositories (DGR) for nuclear waste, repeated glaciations could occur within the time frame relevant to their long-term post-closure safety (up to 1 million years; Myr). Ice sheets can affect the long-term safety of a DGR by elevating the hydrostatic pressure at DGR depth, altering groundwater flow and chemistry, influencing the frequency and severity of earthquakes, and causing surface bedrock erosion. Therefore, DGR safety assessments must account for uncertainties in future ice-sheet variability, including the timing, frequency and duration of ice sheets at the DGR site. Using coupled ice sheet-climate models to constrain uncertainties in ice-sheet variability over the next 1 Myr is not feasible due to the long timescales involved and substantial computational requirements. Instead, we propose a simplified methodology to assess future ice-sheet variability at potential DGR sites using reconstructions of past ice sheets and global simulations of future climate change. The simulations are conducted using a conceptual climate model driven by changes in insolation and atmospheric CO₂ concentrations resulting from anthropogenic emissions. The model is calibrated with 500 000 years (500 kyr) of climate proxy data inferred from deep-ocean sediments.

Applying this methodology to the planned Swedish DGR site intended for disposal of spent nuclear fuel in Forsmark suggests that the onset of the next glaciation at the site will not occur until 100 kyr after present, even in the absence of anthropogenic CO₂ emissions. However, anthropogenic emissions have the potential to delay the next glaciation in Forsmark by several hundred thousand additional years. Following the initial glaciation, our results suggest that the frequency and duration of subsequent glaciations in Forsmark resemble those observed over the last 800 kyr. Considering uncertainties in anthropogenic emissions and future climate evolution, a wide range of possible future glacial developments is identified. At the extremes of this uncertainty range – developments with a low likelihood of occurrence but relevant for evaluating the robustness of the DGR – we find that Forsmark could experience ice-sheet coverage for nearly half of the next 1 Myr or remain almost entirely ice-free throughout this period. The proposed methodology is easy to implement and applicable to any potential DGR site with a recorded history of glaciations.

1 Introduction

Many countries plan to adopt a deep geological repository (DGR) as a safe disposal system to contain and isolate nuclear waste for an extended period of time, up to 1 million years (Myr) for spent nuclear fuel (NEA, 2009; Kim et al., 2011). The long-term post-closure safety of a DGR depends on effective engineered barriers and stable surrounding conditions in e.g. the geosphere (IAEA, 2003). In order to obtain licences for constructing and operating such facilities, assessments of long-term DGR safety must demonstrate that the engineered barriers can withstand a wide range of potential events and developments over the next 1 Myr (IAEA, 2012). This includes impacts from changes in the climate conditions, such as freezing from permafrost and increased hydrostatic pressure from potential ice sheets over the DGR site. In addition, future ice-sheet variability should be considered, as it may significantly impact the conditions in the geosphere. For example, the duration of glaciations affects groundwater chemistry, such as salinity and oxygen content, which may impact the integrity of the engineered barriers (SKB, 2022). Moreover, when the margin of an ice sheet is situated in close proximity to the DGR, the groundwater flow may substantially increase (Vidstrand et al., 2013), facilitating transport of the low-saline and oxygen-rich groundwater toward the DGR. Glaciations also affect the stress distribution within the solid Earth, potentially influencing the frequency and severity of earthquakes (Lund et al., 2009), as well as the magnitude of surface bedrock erosion, which over time brings the DGR closer to the surface (Hall et al., 2019; Krabbendam et al., 2022). Finally, ice sheets can also lead to stronger fluvial bedrock erosion during periods of deglaciation (e.g., Piotrowski, 1994).

Evidence of extensive glaciations on Earth can be found in the geological records. Figure 1 presents an example of such a record, depicting variations in the ratio of heavy to light oxygen isotopes (δ¹⁸O¹) throughout the Pleistocene era (approximately 2.6 Myr to 11 thousand years (ka) ago), as inferred from deep-ocean sediments (Lisiecki and Raymo, 2005). δ¹⁸O serves as a proxy for global ice volume (sea level) and temperature, with high δ¹⁸O values corresponding to cold glacial conditions with extensive land ice (low sea level) and low values corresponding to warm interglacial conditions with limited ice cover (high sea level). Figure 1 shows a long-term cooling trend throughout the early Pleistocene, likely attributed to a long-term decrease of atmospheric CO₂ (e.g. Clark et al., 2006; Willeit et al., 2019). In addition, Fig. 1 highlights two prominent features of past glacial-interglacial cycles. Firstly, a significant shift known as the mid-Pleistocene transition occurred around 1.2–0.8 Myr ago (shading in Fig. 1). Prior to this transition, glacial cycles had a characteristic period of approximately 40 kyr, which extended to around 100 kyr after the transition. Secondly, δ¹⁸O variations exhibited greater amplitude during the 100 kyr cycles compared to the 40 kyr cycles, indicating that ice-sheet extents during the later Pleistocene were larger than those during the early Pleistocene. It can be noted that the last glacial cycle (approximately the last 120 kyr) represents one of the most extensive glaciations recorded in deep-ocean sediments (Fig. 1). At the Last Glacial Maximum (LGM) around 20 kyr ago, ice sheets reached their maximum extents of that glacial cycle, covering regions such as the Nordic countries and Canada as well as parts of present-day United Kingdom, Ireland, Germany, Poland, and the USA (e.g., Clark and Mix, 2002).

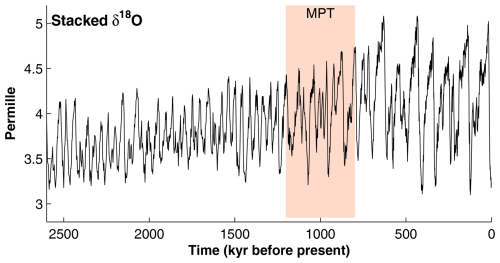
Figure 1 Stack of 57 records of oxygen isotope ratios (δ¹⁸O; unit ‰) for the last 2.6 Myr, inferred from deep-ocean sediments (Lisiecki and Raymo, 2005). δ¹⁸O serves as a proxy for global ice volume and temperature. The coloured shading marks the timing of the mid-Pleistocene transition (MPT). The LGM corresponds to most recent local δ¹⁸O maximum, occurring around 20 kyr BP.

The primary driver of Earth's climate over glacial-interglacial timescales is the latitudinal and seasonal distribution of incoming solar radiation (insolation), which varies due to changes in the Earth's orbit. These orbital variations include changes in eccentricity (∼ 400 and ∼ 100 kyr cycles), obliquity (∼ 41 kyr cycles), and precession of the equinoxes (∼ 23 kyr cycles) (e.g., Berger, 1988). In addition to insolation variations, the dynamics of glacial-interglacial cycles are modulated by complex interactions among Earth system components, such as ice sheets, atmosphere and ocean circulations, the lithosphere and the carbon cycle. Whilst the role of these interactions in the overall dynamics of glacial cycles (cf. Fig. 1) has been relatively well studied (e.g., Oerlemans, 1980; Pollard, 1982; Deblonde et al., 1992; Ganopolski and Calov, 2011; Abe-Ouchi et al., 2013: Ganopolski and Brovkin, 2017: Watanabe et al., 2023), our understanding of their impact on the regional ice-sheet evolution remains limited, complicating efforts to assess future ice-sheet variability over a potential DGR site.

Assessing future ice-sheet variability is further complicated by anthropogenic impacts on the climate system. It has been found that the onset of a glacial cycle (glacial inception) is primarily driven by summer insolation and prevailing atmospheric CO₂ levels (Ganopolski et al., 2016). Specifically, sufficiently low CO₂ levels combined with reduced summer insolation at high latitudes lead to an initial ice growth on the continents. This initial ice growth triggers further decreases in atmospheric CO₂ due to climate-carbon cycle feedbacks, leading to additional cooling and ice expansion (e.g., Lüthi et al., 2008; Brovkin et al., 2012).

In absence of anthropogenic CO₂, the next global glacial inception is projected to occur in approximately 50 kyr (Berger and Loutre, 2002; Archer and Ganopolski, 2005; Cochelin et al., 2006; Ganopolski et al., 2016; Talento and Ganopolski, 2021). However, studies indicate that a small fraction of current anthropogenic CO₂ emissions can persist in the atmosphere for several hundred thousand years (Colbourn et al., 2015; Lord et al., 2016; Jeltsch-Thömmes and Joos, 2020). As a result, model projections suggest that the next glacial inception may be delayed by several hundred thousand years due to anthropogenic emissions (Archer and Ganopolski, 2005; Lord et al., 2015, 2019; Talento and Ganopolski, 2021; Williams et al., 2022).

One approach for projecting ice-sheet variability involves simulations using comprehensive ice-sheet and climate models. This approach has been used for the last glacial cycle (Abe-Ouchi et al., 2013). These comprehensive models typically exhibit high complexity, aiming to resolve most of the known processes and interactions within the climate system. However, despite their complexity, they are limited by our incomplete understanding of glacial dynamics, resulting in that several parameters are poorly constrained. Furthermore, the computational demands of such models are substantial, making it time-consuming to perform numerous simulations to address these uncertainties. In this study, we therefore propose an alternative methodology to assess future ice-sheet variability at potential DGR sites using a simplified framework, consisting of conceptual modelling and geological data. Despite its simplicity, our methodology is designed to effectively capture identified uncertainties in anthropogenic emissions and future climate evolution. To demonstrate the applicability of the methodology, we apply it to Forsmark, the planned DGR site for spent nuclear fuel in Sweden. Forsmark is situated on the coast in south-central Sweden, at approximately 60° N.

The paper is organised as follows. The proposed methodology for projecting future ice-sheet variability at a DGR site is presented in Sect. 2. The resulting frequency and duration of glaciations in Forsmark over the next 1 Myr, using this methodology, is presented in Sect. 3. Finally, Sect. 4 contains the conclusions as well as a discussion about the limitations and possibilities of the proposed methodology.

2 Methodology

The proposed methodology for estimating future ice-sheet variability at potential DGR sites is outlined in Fig. 2. This approach relies on conceptual modelling to project global climate change and utilises geological data of past glaciations to identify potential thresholds in the global climate that correspond to glaciations at the DGR site. The conceptual model, along with its calibration and the simulations performed, is detailed in Sect. 2.1. The conceptual model and the modelling approach adopted here is identical to that of Lord et al. (2019), so the reader is referred to that publication for further details. The methodology for defining global thresholds using data of past glaciations is described in Sect. 2.2, with Forsmark serving as an example.

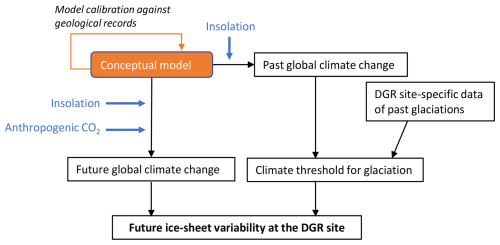
Figure 2 Schematic illustration of the proposed methodology for assessing future ice-sheet variability at potential DGR sites.

2.1 Conceptual model

2.1.1 Model description

The conceptual model in this study (Lord et al., 2019) is based on the insolation-threshold model of Archer and Ganopolski (2005), which itself was developed from the model of Paillard (1998). The model predicts transitions between three climate regimes: interglacial, mild glacial and full glacial, based on prevailing insolation and global ice volume. These transitions occur when the insolation or ice volume crosses certain predefined thresholds. The model solves a set of ordinary differential equations, enabling climate projections over timescales up to 1 Myr to be generated within seconds on a standard computer. The efficiency of the model allows for multiple simulations with different parameter combinations, facilitating a systematic exploration of the parameter space in order to account for uncertainties in future climate evolution.

The primary forcing for the model is the northern hemisphere high-latitude summer insolation, here defined as the average between 21 June and 20 July at 65° N using the orbital solution of Laskar et al. (2004). The model calculates the normalised global ice volume, v, based on changes in insolation, with v=0 representing an interglacial state and v=1 a fully-glacial state. The model contains eight tunable parameters (Table S1 in the Supplement). One of these parameters, the critical insolation threshold (i0), determines transitions from an interglacial to a mild glacial state. In future projections, this parameter is adjusted to account for anthropogenic CO₂ perturbations in the atmosphere, following the methodology outlined by Archer and Ganopolski (2005). In their study, several simulations using the CLIMBER-2 Earth System Model of intermediate complexity were used to estimate the relationship between i0 and anthropogenic CO₂ perturbations.

2.1.2 Model calibration

To ensure that the model accurately captures the timing and variability of past glacial cycles, it is calibrated against δ¹⁸O data inferred from deep-ocean sediments (Fig. 1; Lisiecki and Raymo, 2005). To facilitate comparison between the projected normalised ice volumes and the δ¹⁸O data, both are converted to global-mean surface air temperature change (ΔT) using a linear scaling. Specifically, the change in modelled ΔT is assumed to scale linearly with the normalised ice volume, such that $\mathrm{\Delta }T=-$4 °C corresponds to the normalised ice volume at the LGM and ΔT=0 °C corresponds to normalised ice volume at present-day. The cold anomaly of −4 °C is obtained from the reconstructed global-mean surface air temperature anomaly at the LGM (Annan et al., 2022). Similarly, the δ¹⁸O records are converted to ΔT by assigning the maximum δ¹⁸O value during LGM to −4 °C and the present-day value to 0 °C. As mentioned in the introduction, the deep-ocean δ¹⁸O signal provides information on changes in both global sea level and temperature. Scaling the δ¹⁸O records with respect to temperature alone is justified by a demonstrated strong correlation between changes in ΔT and global sea levels on longer timescales (de Boer et al., 2010). This correlation is physically reasonable because colder climates typically lead to more extensive ice sheets (lower sea levels), which in turn further cool the climate through various feedback mechanisms.

Five of the eight tunable model parameters (1, 2, 4, 5 and 8; see Table S1) significantly affect the simulated ice volume, whereas the model is relatively insensitive to the remaining three parameters (Paillard, 1998; Lord et al., 2019). Consequently, these five parameters are varied randomly and concurrently using Latin hypercube sampling, producing 1000 different sets of values for the five parameters. The conceptual model is then run using each sample set in turn, and the results are compared to the last 500 kyr of the δ¹⁸O data (Fig. 1). Thus, the model is calibrated using glacial-interglacial cycles with a characteristic period of approximately 100 kyr. The underlying assumption, therefore, is that the overall variability of future glaciations will be similar to that of the most recent cycles. Simulations that successfully project a full glacial regime (see Sect. 2.1.1) around the time of the LGM and exhibit a sufficiently low root mean squared error (RMSE) with respect to the δ¹⁸O data are retained², while the remaining simulations are excluded (see Sect. 3.1.3 in Lord et al., 2019 for details). This process results in the retention of 90 out of the original 1000 simulations. The projected ΔT from the retained simulations is depicted in Fig. 3 (grey lines), alongside ΔT estimated from the stacked δ¹⁸O data (orange line). As shown in the figure, discrepancies between simulations and observations occur at a few intervals such as 500–480, 380–360, and 175–150 kyr BP. However, a side from these differences, the simulations broadly capture the variability of the geological data over the last 500 kyr. This includes known periods of cold glacial conditions such as the penultimate glacial maximum (∼ 140 kyr ago) and the LGM (∼ 20 kyr ago), as well as warm interglacial periods, like the Eemian (∼ 125 kyr ago) and the current Holocene interglacial (last ∼ 11 kyr).

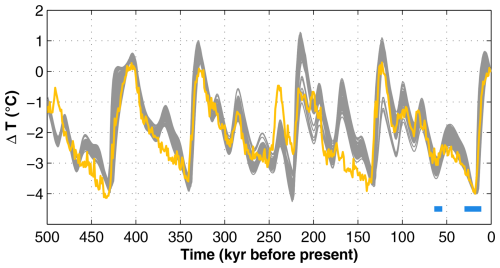
Figure 3 Time series of the global-mean surface air temperature change (ΔT). Grey lines depict ΔT from 90 calibrated simulations using the conceptual model, and the orange line shows reconstructed ΔT from δ¹⁸O data (Lisiecki and Raymo, 2005). Blue horizontal lines indicate reconstructed periods of ice-sheet coverage in Forsmark during the last glacial cycle (Fig. S2).

2.1.3 Future projections

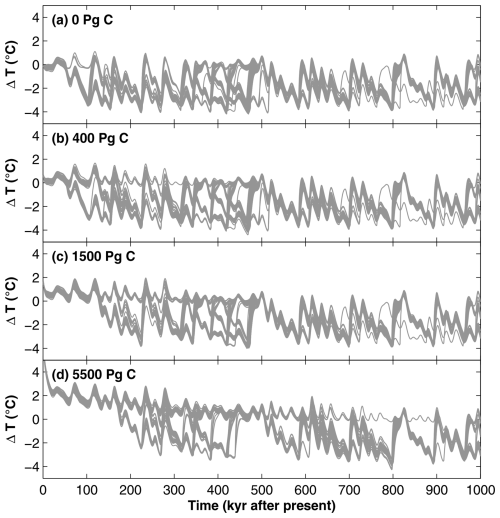
To project the future climate evolution, the 90 calibrated models are integrated 1 Myr into the future. The future evolution of summer insolation is calculated using the solution of Laskar et al. (2004) (Fig. S1a) and four scenarios of anthropogenic CO₂ emissions are considered, amounting to approximately 0, 400, 1500 and 5500 petagrams of carbon (Pg C). For context, 400 Pg C approximately corresponds to the anthropogenic carbon emissions emitted up to today. The 1500 Pg C scenario is broadly consistent with the SSP2-4.5 scenario of the Intergovernmental Panel on Climate Change (IPCC, 2021) as well as with recent “business as usual” scenarios, which assume that currently stated policies for transitioning away from fossil fuels will be implemented but no policies will be added beyond that (IEA, 2023). Finally, the 5500 Pg C scenario is consistent with the worst-case scenario examined by the IPCC (SSP5-8.5), assuming a rapid exploitation of fossil fuels within this century.

Using these cumulative emissions, a carbon cycle impulse response function (IRF) is employed to generate atmospheric CO₂ concentration data for the next 1 Myr. The IRF was developed based on an ensemble of simulations run using the cGENIE Earth system model of intermediate complexity (Ridgwell and Hargreaves, 2007; Colbourn et al., 2013), with total anthropogenic CO₂ emissions ranging from 1000 to 20 000 Pg C (Lord et al., 2016). Under the assumption that all emissions are released at present day³, the IRF projects that CO₂ concentrations peak immediately upon the release, and then gradually decrease back towards the pre-industrial atmospheric CO₂ concentration (280 ppmv) over the next 1 Myr (Fig. S1b), as various carbon cycle processes remove excess CO₂ from the atmosphere. For the 0 Pg C scenario, the atmospheric CO₂ concentration is maintained at 280 ppmv throughout the entire future period of 1 Myr. As a result, future climate projections in this scenario are driven solely by changes in insolation. Natural CO₂-climate feedbacks, which have been observed during past glacial cycles (e.g., Lüthi et al., 2008), are not explicitly included in the modelling. However, because the model was calibrated using δ¹⁸O data (Fig. 1) – whose variability partly reflects these feedbacks – they are implicitly considered in the future projections.

The evolution of ΔT (compared with pre-industrial, i.e., ΔT=0 °C) over the next 1 Myr is shown in Fig. 4 across all 90 simulations and examined emissions scenarios. Overall, these results are in line with previous studies on long-term future climate evolution (e.g., Archer and Ganopolski, 2005; Ganopolski et al., 2016). Under the 0 and 400 Pg C scenarios, the temperature is projected to remain relatively stable for at least the next 50 kyr, after which most of the simulations project a global cooling due to a significant decline in summer insolation. Conversely, in the 1500 and 5500 Pg C scenarios, atmospheric CO₂ concentrations remain sufficiently elevated for the first 100 kyr (Fig. S1b), such that the onset of the next major cooling event is delayed until after 100 kyr in all 90 simulations (Fig. 4).

Figure 4 Projected ΔT over the next 1 Myr for (a) 0 Pg C, (b) 400 Pg C, (c) 1500 Pg C and (d) 5500 Pg C emissions scenarios for each of the 90 calibrated configurations of the conceptual model.

2.2 Temperature threshold for glaciation (ΔT_threshold)

The observed strong correlation between ΔT and global sea level (de Boer et al., 2010) suggests that lower ΔT values correspond to more extensive glaciations, increasing the likelihood that a specific location in the mid to high latitudes will be covered by an ice sheet. To project future glaciations at potential DGR sites, our key assumption is that as the climate becomes gradually colder, ΔT will eventually reach a threshold, ΔT_threshold, beyond which the glaciation will be extensive enough to cover the site with an ice sheet. To constrain potential values of ΔT_threshold, site-specific data of past glaciations are necessary. One example of such data, used throughout this study, is an ice-sheet reconstruction of the last glacial cycle for the planned Swedish DGR site in Forsmark. According to this reconstruction, Forsmark was covered by an ice sheet during two distinct phases of the last glacial cycle: from 64 to 55 kyr and from 30 to 11 kyr before present (Fig. S2), with the latter period incorporating the LGM. This reconstruction is based on ice-sheet modelling, where the modelled ice-sheet extents were calibrated against information on past glacial marginal positions interpreted from geological data. In this reconstruction, the general evolution of the Eurasian ice sheet (see Fig. 3-15 in SKB, 2020) is consistent with other ice-sheet reconstructions (Svendsen et al., 2004; Batchelor et al., 2019) and aligns broadly with the reconstructed climate evolution in northern Europe during this period (Helmens, 2014). Besides the last glacial cycle, there is also evidence that the Forsmark site was covered by an ice sheet during preceding glaciations, for example during the penultimate glacial maximum (Svendsen et al., 2004). However, the timings of these earlier glaciations are highly uncertain and are therefore omitted from the calculation of ΔT_threshold.

Comparing the reconstructed periods of Forsmark glaciation (Fig. S2) with the global simulations of past ΔT evolution (Fig. 3), it is evident that the reconstructed periods of past glaciations, as anticipated, coincide with local minima in ΔT (Fig. 3, blue horizontal lines). To determine the value of ΔT_threshold, we first assume that the ice-sheet reconstruction for the Forsmark site is an adequate representation of the past. Then we examine how many simulations project two periods of glaciation in Forsmark during the last glacial cycle (from 120 kyr ago up to present day) for different values of this threshold. In this exercise, glaciation is assumed to occur when ΔT drops below ΔT_threshold. Our results reveal that for only one of the investigated thresholds, $\mathrm{\Delta }{T}_{\mathrm{threshold}}=-$2.8 °C, are both periods of glaciation successfully projected in all 90 simulations (Fig. 5). This value is therefore chosen as the best-estimate ΔT_threshold for Forsmark glaciation.

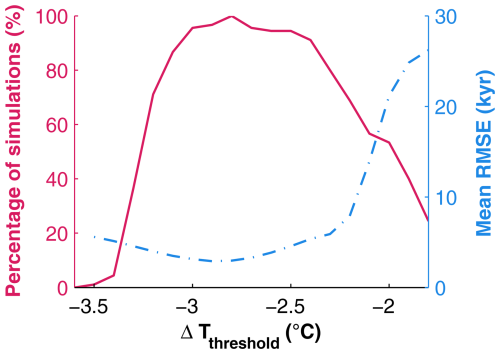
Figure 5 Percentage of simulations across the 90 calibrated model configurations that project two periods of glaciation in Forsmark during the last 120 kyr (red solid line), along with the average RMSE of projected glaciation/deglaciation timings compared to the ice-sheet reconstruction (blue dashed line).

By constraining the best-estimate ΔT_threshold from the reconstructed conditions of the last glacial cycle, we implicitly assume that future regional ice-sheet extents will resemble that of the last glacial cycle. However, geological records indicate that this is not necessarily the case. For instance, evidence shows that the Eurasian ice sheet during the penultimate glacial cycle was significantly larger than during the last glacial cycle (Svendsen et al., 2004), despite exhibiting similar changes in global ice volume (Spratt and Lisiecki, 2016; see also Fig. 1). The underlying reasons for these differences are not known, making it challenging to accurately project regional ice-sheet evolution during future glaciations. To address this uncertainty, a wider range of ΔT_threshold is adopted alongside the best estimate. This range is defined to be roughly compatible with the conditions of the last glacial cycle, while also allowing for a wide variety of alternative ice-sheet developments. Specifically, the range encompasses all values of ΔT_threshold that meet the following two criteria; (i) at least one of the 90 simulations must project two periods of glaciation during the last glacial cycle, and (ii) the projected glacial periods must, at least marginally, overlap with the corresponding periods in the Forsmark reconstruction. The latter criterium is evaluated by measuring the average RMSE of the projected timings of glacial periods across the 90 simulations with respect to those of the reconstruction. An overlap between projected and reconstructed glacial periods is only deemed possible if the RMSE is lower than the maximum duration of ice-sheet coverage in the reconstruction (19 kyr). Using these two criteria, the lowest potential ΔT_threshold is −3.5 °C, as no simulations yield two glaciations in Forsmark for lower values, and the highest potential ΔT_threshold is −2.1 °C, as the RMSE exceeds 19 kyr for higher values (Fig. 5). Low-end values of ΔT_threshold suggest that Forsmark will only become glaciated once the ice sheets have nearly reached their maximum extents. This could occur if the ratio of ice in North America to that in Eurasia is higher during future glacial cycles than it was during the last glacial cycle, or if the Eurasian ice sheet primarily expands eastward or westward instead of southward throughout most of the glacial cycle. Conversely, high-end values of ΔT_threshold imply that Forsmark will be glaciated at relatively low global ice volumes. This situation could arise if future glaciations are characterised by greater ice growth in Eurasia and less in North America compared to the last glacial cycle, i.e., similar to the conditions observed during the penultimate glacial cycle.

3 Results – frequency and duration of future ice sheets in Forsmark

In this section, we analyse the resulting frequency and duration of future ice sheets in Forsmark using future ΔT projections (Sect. 2.1.3) and the estimated thresholds for glaciation, ΔT_threshold (Sect. 2.2). We consider four variables that characterise future ice-sheet variability in Forsmark over the next 1 Myr;

1. Timing of the next glaciation (t_glac): defined as the first future occurrence when projected ΔT drops below ΔT_threshold.

2. Number of glaciations (n_glac): defined as the number of times projected ΔT drops below ΔT_threshold.

3. Maximum duration of an individual glaciation (d_ind): defined as the longest uninterrupted period during which ΔT remains below ΔT_threshold.

4. Total duration of glaciations (d_tot): defined as the total time during which ΔT is below ΔT_threshold.

All four variables are of relevance for the long-term safety of a DGR. For example, t_glac helps to estimate the remaining radioactivity in the nuclear waste when the site first encounters an ice-sheet passage. n_glac is important because each ice-sheet passage significantly increases groundwater flow in the geosphere and affects surface denudation. Additionally, d_ind and d_tot may influence both surface denudation and geochemical conditions.

3.1 Ice sheet variability using best-estimate ΔT_threshold

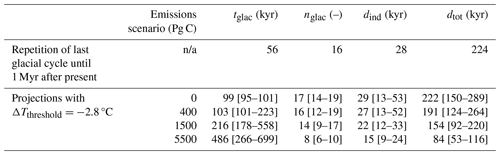
Projections of ice-sheet variability for the next 1 Myr in Forsmark, using the best-estimate ΔT_threshold, are presented in Table 1 for each considered CO₂ emissions scenario. The values outside the brackets represent the median, while those inside the brackets show the 5th to 95th percentile ranges of t_glac, n_glac, d_ind, and d_tot across the 90 simulations. The table also features a hypothetical scenario which assumes that all future glaciations are identical to those of the last glacial cycle. In this reference case, it is thus assumed that the conditions of the last 120 kyr, including the two periods of glaciation, are repeated from the present day until 1 Myr into the future.

Table 1 Projected t_glac, n_glac, d_ind and d_tot in Forsmark over the next 1 Myr, calculated using the best-estimate threshold for glaciation ($\mathrm{\Delta }{T}_{\mathrm{threshold}}=-$2.8 °C). The values outside the brackets show the median projection across the 90 simulations, whereas the values inside the brackets represent the 5th–95th percentile range of the simulations. For reference, corresponding projections for a hypothetical scenario where the last glacial cycle (last 120 kyr) is repeated 1 Myr into the future are also shown.

3.1.1 The 0 Pg C scenario

For the 0 Pg C scenario, the median projections for n_glac, d_ind, and d_tot are very similar to the hypothetical case of repeating last glacial cycle conditions over the next 1 Myr (Table 1). This similarity is anticipated, given that the best-estimate ΔT_threshold was derived from the conditions of the last glacial cycle. However, for the timing of the next glaciation at the site (t_glac), projections indicate a delay of approximately 50 kyr compared to the first glaciation in the last glacial cycle. This delay is attributed to the next 50 kyr being characterised by relatively low summer-insolation variability, a condition not present during the onset of the last glacial cycle (Berger and Loutre, 2002). The delayed onset of the next glaciation is a consistent feature across the simulations, with t_glac demonstrating a narrow 5–95th percentile range of 6 kyr. In contrast, projections for n_glac, d_ind, and d_tot exhibit greater variability across the simulations. This is particularly notable for d_ind, which has a 5–95th percentile range of 40 kyr (Table 1).

3.1.2 Effect of anthropogenic emissions

Our projections indicate that higher anthropogenic emissions lead to a delayed onset of the next glaciation in Forsmark, as indicated by increasing values of t_glac for higher emissions scenarios (Table 1). This result is consistent with previous studies evaluating the timing of the next glacial inception (e.g., Archer and Ganopolski, 2005; Lord et al., 2015; Ganopolski et al., 2016). Whilst the delayed glaciation is most pronounced for 1500 and 5500 Pg C scenarios, some simulations under the 400 Pg C scenario also project that an ice sheet will not return to Forsmark within the next 200 kyr. This suggests that the carbon emissions released by humans to date may have contributed to delaying the next glaciation in Forsmark by up to 100 kyr.

The delayed onset of the next glaciation due to anthropogenic emissions results in an anticipated reduction of n_glac and d_tot (Table 1). This trend is also observed for d_ind, which is notably reduced under the 1500 and 5500 Pg C scenarios. This result is somewhat surprising given that the projections exhibit similar variability across all emissions scenarios towards the end of the 1 Myr period (Fig. 4), when the impact of emissions has diminished (Fig. S1b). However, the longest durations of individual glaciations typically occur between 300 and 500 kyr after present in the simulations, prior to the first glaciation in many of the high-emission simulations. During this period, insolation variations are relatively small (Fig. S1a), so if ΔT drops below ΔT_threshold, Forsmark may remain glaciated for an extended period.

3.2 Sensitivity to ΔT_threshold

Next, we examine how the uncertainty in ΔT_threshold affects the frequency and duration of future glaciations in Forsmark. Figure 6 shows the projected t_glac, n_glac, d_ind, and d_tot as functions of potential ΔT_threshold values, which range from −3.5 to −2.1 °C (Sect. 2.2). The results are presented for both extreme emissions scenarios, 0 and 5500 Pg C, to identify the most extreme potential cases of future glaciations, or lack thereof, at the Forsmark site.

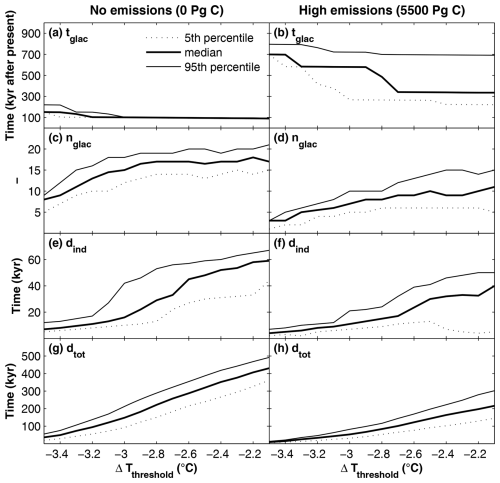
Figure 6 Projected t_glac (a, b), n_glac (c, d), d_ind (e, f) and d_tot (g, h) for Forsmark over the next 1 Myr as a function of ΔT_threshold. The results are shown for the 0 (left panels) and 5500 Pg C scenarios (right panels), with median projections (thick solid line) and 5th (dashed thin line) and 95th (thin solid line) percentiles across the 90 simulations.

For the 0 Pg C scenario, we find that t_glac is highly insensitive to the value of ΔT_threshold. Except for very low values of ΔT_threshold, n_glac also shows little change. This suggests that variations in the regional ice-sheet distribution during future glacial cycles, in absence of anthropogenic emissions, are not of critical importance for the timing of the first glaciation or the frequency of glaciations in Forsmark. However, unlike t_glac and n_glac, the projected durations (d_ind, and d_tot) increase notably with ΔT_threshold in the 0 Pg C scenario. In the most extreme case, with the highest identified values of ΔT_threshold, projections of d_ind, and d_tot reach almost 70 and 500 kyr, respectively (Fig. 6e, g).

In stark contrast to the largely ice-sheet dominated futures featured in the 0 Pg C scenario, our results for the 5500 Pg C scenario suggest that anthropogenic emissions could lead to mostly ice-free conditions in Forsmark over the next 1 Myr. This possibility persists regardless of ΔT_threshold, as shown by the 95th percentile projection of t_glac, which remains around 700–800 kyr for all investigated values of ΔT_threshold (Fig. 6b). In contrast, the median projection of t_glac decreases from approximately 700 to 300 kyr as ΔT_threshold increases. This decrease is reflected in the d_tot projections, which typically range from a few tens of thousands of years for the lowest ΔT_threshold values to approximately 200 kyr for the highest values (Fig. 6h).

4 Discussion and concluding remarks

The potential for future glaciations is a key concern for the long-term safety of a DGR located in the mid to high latitudes. We have developed a simplified methodology to project the frequency and duration of ice sheets over a site that has a recorded history of glaciations. Our approach integrates modelling and observational data into a straightforward framework, consisting of a conceptual model that captures the temporal evolution of global climate change and timings of past glaciations from observational data and/or modelling. A major advantage of our methodology is that it accounts for uncertainties in both future climate evolution and anthropogenic emissions without requiring time- and resource-intensive modelling, such as simulations with coupled ice sheet-climate models.

While straightforward, the methodology also possesses some notable limitations. First, the overall variability of future glaciations projected by the conceptual model mirrors the glacial cycles used for calibration. In our case, the model was calibrated with data covering the last 500 kyr, a period dominated by glacial-interglacial cycles with a characteristic timescale of 100 kyr. However, deep-ocean δ¹⁸O data shows that glaciations occurring before the mid-Pleistocene transition were characterised by shorter cycles of approximately 40 kyr. The cause of the mid-Pleistocene transition is not known (Berends et al., 2021; Herbert, 2023), adding uncertainty to the overall variability of future glaciations, especially given that the past 40 kyr cycles occurred during warmer climates with similar temperatures to some of those projected for the future. Capturing interactions that could alter the variability of future glacial cycles requires the use of a more comprehensive model than the one employed here. Second, there are considerable uncertainties in the timing of past glaciations at the DGR site, which is crucial for constraining the threshold for glaciation (ΔT_threshold) in this study. This uncertainty is particularly pronounced for glaciations prior to the LGM, as they are generally older than the effective range of the C-14 dating method (∼ 55 kyr; Reimer et al., 2020). To mitigate this issue, we have placed greater emphasis on metrics that are independent of the precise timing of these glaciations. For instance, our best-estimate ΔT_threshold is determined based on the number of projected glaciations over the past 120 kyr, rather than the exact timing of these glaciations.

Applying the proposed methodology to the planned Swedish DGR site, Forsmark, suggests that over the next 1 Myr, there will likely be a slightly reduced frequency and duration of glaciations compared to a case of repeating the reconstructed last glacial cycle over this period. This reduction is primarily due to a delay in the onset of the next global glaciation, caused by anthropogenic carbon emissions and low insolation variability during the first 50 kyr after present. Under the 1500 Pg C scenario, which can be considered a likely scenario given current climate policies, our results indicate that the next glaciation in Forsmark will not occur for at least 200 kyr, and possibly even several hundred thousand years longer than this, depending on the extent to which remaining anthropogenic CO₂ inhibits the next glacial inception. Uncertainty in future atmospheric CO₂ concentrations is also amplified by the possibility that humans will implement some form of Carbon Dioxide Removal (CDR) in the future (Keller et al., 2018).

Considering the full range of uncertainties in anthropogenic emissions and future climate evolution reveals a wide spectrum of possible outcomes, some of which diverge significantly from the likely scenario depicted above. At the extremes of this uncertainty range, the Forsmark site could experience ice-sheet coverage for nearly half of the next 1 Myr or remain almost entirely ice-free throughout this entire period. We believe both of these extremes have a low likelihood of occurrence. Furthermore, the significance of these scenarios for post-closure DGR safety may also depend on other factors unrelated to climate and ice sheets. For example, if Forsmark were to be covered by an ice sheet for half the assessment period of 1 Myr, the bedrock would likely be significantly depressed due to the ice load, submerging the DGR area beneath the sea for significant portions of the time with ice-free conditions. This would in turn prevent human settlements from establishing in the area, thereby reducing the risk that any potential leakage of radionuclides from the DGR could have a detrimental impact on human health. Conversely, shorter periods of ice-sheet coverage may lead to less bedrock sinking. This would in turn create opportunities for human use of the landscape around the DGR during the relatively long ice-free intervals between glaciations, potentially increasing the risk of higher radiological exposure due to a potential leak from the DGR.

In summary, we have developed a new methodology for assessing frequency and duration of future ice sheets at potential DGR sites with a recorded history of glaciations. This methodology combines conceptual modelling, which can be easily implemented on a standard computer, with site-specific data of past glaciations. Data of projected atmospheric CO₂ concentrations, which we obtained from external modelling efforts (Lord et al., 2016), is preferable for exploring likely future developments but not strictly necessary for examining extreme scenarios, which are valuable for evaluating the robustness of a DGR. For instance, assuming no anthropogenic emissions can be considered a sound approach when estimating the earliest possible occurrence or the maximum possible frequencies and durations of future glaciations at a certain site. Furthermore, since we have shown that Forsmark, located at 60° N in a region exposed to numerous Pleistocene glaciations, may experience predominantly ice-free conditions over the next 1 Myr, this will likely be the case for other potential DGR sites, most of which are located south of 60° N. This also implies that if data on past glaciations are unavailable for a site south of 60° N, the projected frequencies and durations of future glaciations in Forsmark presented here could potentially serve as a conservative upper-bound estimate for that location.