Uranium migration through the Swiss Opalinus Clay varies on the metre scale in response to differences of the stability constant of the aqueous, ternary uranyl complex Ca₂UO₂(CO₃)₃

The simulation of uranium migration through the Swiss Opalinus Clay is used as an example to quantify the influence of varying values of a stability constant in the underlying thermodynamic database on the migration lengths for the repository scale. Values for the stability constant of the neutral, ternary uranyl complex Ca₂UO₂(CO₃)₃ differ in literature by up to one order of magnitude. Within the studied geochemical system, either the neutral or the anionic complex ${\mathrm{CaUO}}_{\mathrm{2}}({\mathrm{CO}}_{\mathrm{3}}{)}_{\mathrm{3}}^{\mathrm{2}-}$ is the predominant one, depending on the chosen value for the neutral complex. This leads to a changed interaction with the diffuse double layers (DDL) enveloping the clay minerals and thus can potentially influence the diffusive transport of uranium. Hence, two identical scenarios only differing in the value for the stability constant of the Ca₂UO₂(CO₃)₃ complex were applied in order to quantify and compare the migration lengths of uranium on the host rock scale (50 m) after a simulation time of one million years. We ran multi-component diffusion simulations for the shaly and sandy facies in the Opalinus Clay. A difference in the stability constant of 1.33 log units changes the migration lengths by 5 to 7 m for the sandy and shaly facies, respectively. The deviation is caused by the anion exclusion effect. However, with a maximum diffusion distance of 22 m, the influence of the stability constant of the Ca₂UO₂(CO₃)₃ complex on uranium migration in the Opalinus Clay is negligible on the host rock scale.

1 Introduction

Safety of a repository is based to a large extent on the isolation of the radioactive waste within a suitable host rock (IAEA, 2003). Clay rocks provide an option due to their high retention capacity against radionuclides and very low hydraulic conductivity only allowing diffusive transport. However, diffusion processes in clay formations are complex due to the diffuse double layers (DDL) enveloping the clay minerals and the associated different migration behaviour for cationic, anionic and neutral species (Van Loon and Soler, 2003; Appelo and Wersin, 2007; Appelo et al., 2010). The DDL compensates the net surface charge resulting from the contact between pore water and external surfaces of the clay minerals by attraction of counter-ions and repulsion of co-ions and affects thereby their diffusive transport (Wersin et al., 2008). Therefore, determination of the speciation of an element in the pore water is crucial to quantify migration distances precisely.

To cover the spatial and temporal scales required for safety assessments, reactive transport simulations are a powerful tool to quantify transport of sorbing radionuclides considering the geochemical conditions within the system. They are based to a large extent on the use of chemical thermodynamic databases. Consequently, in addition to completeness, the selection of the data itself is also important as often various values dependend on the applied experimental conditions are given in literature (Thoenen et al., 2014; Mühr-Ebert et al., 2019). Because varying stability constants within the law of mass action change the overall aqueous species distribution and predominant species, the maximum migration distance of a radionuclide through a clay formation might be affected.

In the present study, we assess this influence for the example of uranium, one of the main components in spent fuel, in the Swiss Opalinus Clay, a potential host rock for the disposal of nuclear waste. For this, we perform multi-component diffusion simulations on the host rock scale (50 m) accounting for the interaction with the DDL as well as for the mineralogical heterogeneity between the shaly and sandy facies. In this geochemical system, uranium is mainly present as U(VI) in ternary uranyl complexes with calcium and carbonate (Hennig et al., 2020).

In previous numerical studies (Hennig et al., 2020; Hennig and Kühn, 2021), that used the PSI/Nagra thermodynamic database (Thoenen et al., 2014) with a logk of 29.22 for the neutral complex (Eq. 1), the anionic complex (Eq. 2) was the predominant species in the geochemical system of the Opalinus Clay.

$$\begin{array}{}\text{(1)}& \begin{array}{r}{\displaystyle }\mathrm{2}{\mathrm{Ca}}^{\mathrm{2}+}+{\mathrm{UO}}_{\mathrm{2}}^{\mathrm{2}+}+\mathrm{3}{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\rightleftharpoons {\mathrm{Ca}}_{\mathrm{2}}{\mathrm{UO}}_{\mathrm{2}}({\mathrm{CO}}_{\mathrm{3}}{)}_{\mathrm{3}}\left(\mathrm{aq}\right)\\ {\displaystyle }\mathrm{logk}=\mathrm{29.22}\end{array}\end{array}$$

$$\begin{array}{}\text{(2)}& \begin{array}{r}{\displaystyle }{\mathrm{Ca}}^{\mathrm{2}+}+{\mathrm{UO}}_{\mathrm{2}}^{\mathrm{2}+}+\mathrm{3}{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\rightleftharpoons {\mathrm{CaUO}}_{\mathrm{2}}({\mathrm{CO}}_{\mathrm{3}}{)}_{\mathrm{3}}^{\mathrm{2}-}\left(\mathrm{aq}\right)\\ {\displaystyle }\mathrm{logk}=\mathrm{27.18}\end{array}\end{array}$$

In contrast, in a sorption experiment done for the same system (Joseph et al., 2011), a value of 30.55 for the logk of the neutral complex (Bernhard et al., 2001) was used in the speciation calculations leading to the neutral complex as predominant one. Both complexes, anionic and neutral, cannot be clearly distinguished by the methods usually applied in experiments (Mühr-Ebert et al., 2019). Moreover, Guillaumont et al. (2003) remarked, that the constant of Bernhard et al. (2001) is not precise since the analysis indicates large experimental errors. Therefore, it was not used for the PSI/Nagra database (Thoenen et al., 2014). Thus, the uncertainty regarding the predominant uranium species in the geochemical system of the Opalinus Clay remains.¹

With our one-dimensional, multi-component diffusion models we quantify the influence of the thermodynamic constant of one of the main aqueous uranium species in the studied system, the neutral, ternary uranyl complex Ca₂UO₂(CO₃)₃, on the maximum diffusion length by using two different values for the logk in the underlying thermodynamic database. With this, we demonstrate, what the difference regarding the selected value for the stability constant means in metre on the host rock scale after one million years.

2 Methods

Simulations were performed with the multi-component option in PHREEQC Version 3.5.0 (Parkhurst and Appelo, 2013). The thermodynamic data is based on the PSI/Nagra database version 12/07 (Thoenen et al., 2014). The Davies approach (Davies, 1962) is used for the database to represent ion-ion interactions (Stockmann et al., 2017; Noseck et al., 2018) as ionic strength of the pore waters in the facies does not exceed 0.5 mol/L (Table 1). As already described in Hennig et al. (2020) and Hennig and Kühn (2021), it was updated and supplemented with the sorption data for the hydroxo-complexes of uranium on the inherent clay minerals (Table 1) as well as the self-diffusion coefficients in water D_w (m²/s) required to apply the multi-component option. This means, the uranium carbonate complexes dominating the speciation in the studied system (Joseph et al., 2011, 2013b; Hennig et al., 2020) were not taken into account for sorption. Consequently, the diffusive transport of uranium complexes and their interaction with the DDL governed by the ionic strength becomes more important, what is accounted for by the MC option in PHREEQC. In line with the database, all simulations were conducted for a temperature of 25 ^∘C as it has been shown, that elevated temperatures, for instance relevant for greater depths (Nagra, 2002), can be neglected (Hennig et al., 2020; Hennig and Kühn, 2021). Neither it significantly changes the pore water composition (<5 % for a temperature of 45 ^∘C, Wersin et al., 2016), nor it affects uranium migration up to temperatures of 60 ^∘C (Joseph et al., 2013b). The Pourbaix diagrams (Sect. 3.1) were created with a coupling between PHREEQC and the open source programming language R (De Lucia and Kühn, 2013, 2021).

The model applied here is based on the concepts presented in Hennig et al. (2020) and Hennig and Kühn (2021). Simulations were performed for the shaly and sandy facies of the Opalinus Clay representing higher and lower clay mineral quantities (76 wt. % and 45 wt. %) as well as major differences in the pore water composition as this primarily governs uranium sorption and migration. The initial input parameters are based on analyses from boreholes at the underground research laboratory Mont Terri (Switzerland) and are given in Table 1.

Table 1 Input parameters representing the shaly and sandy facies. Concentrations are given as average values from borehole analyses.

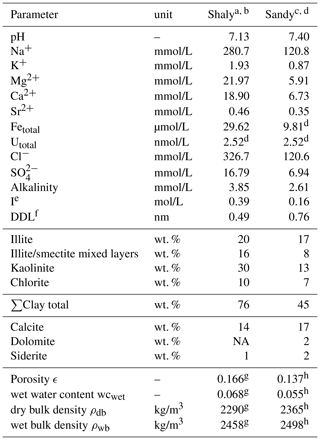
NA = no data available, ^a Vinsot et al. (2008), borehole BPC-C1, ^b Pearson et al. (2003), borehole BPP-1, ^c Wersin et al. (2009), borehole BWS-A3, ^d Pearson et al. (2003), borehole BWS-A3, ^e calculated in PHREEQC, ^f thickness donnan-layer, calculated via ionic strength (Wigger and Van Loon, 2018), ^g Pearson et al. (2003), borehole BWS-A6, ^h Pearson et al. (2003), borehole BWS-E3.

The geochemical behaviour of the Opalinus Clay system and thus speciation as well as sorption of uranium highly depend on the calcite-carbonate ion system (Pearson et al., 2003; Wersin et al., 2009; Hennig et al., 2020). Therefore, we decided to fix the partial pressure of carbon dioxide pCO₂ to 10^−2.2 bar, what corresponds to measured values and is recommended for clay formations with similar mineralogy as the Opalinus Clay (Pearson et al., 2003, 2011; Vinsot et al., 2008; Gaucher et al., 2010; Lerouge et al., 2015). An initial E_H of −227 mV published by Bossart and Thury (2008) was chosen to represent the moderately reducing in-situ conditions (Pearson et al., 2011; Wersin et al., 2011). The pH, pe and the concentrations of the main ions are controlled by means of the fixed pCO₂ via an equilibrium with the present carbonates, calcite, dolomite and siderite, as well as pyrite. The redox couple ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}/{\mathrm{HS}}^{-}$ provides the most consistent results with measured values (Pearson et al., 2003, 2011; Wersin et al., 2009, 2011).

Each facies is represented by an one-dimensional diffusion model consisting of 100 cells a 0.5 m (= 50 m) and corresponds to the transport direction perpendicular to the bedding. Grid independence was confirmed by simulations with finer resolution (0.25 m). Numerical stability is ensured by the Neuman criteria. The source term from the e.g. high-level waste canisters is represented by a Dirichlet boundary condition with a constant uranium concentration of 1 µmol/L (Keesmann et al., 2005; Joseph et al., 2013b), whereas a Neumann boundary is applied to the model outlet. Since our focus lies on the influence of a stability constant on the migration length in the host rock, we do not consider the interaction with the engineered barriers. Hence, our results have to be considered as maximum diffusion lengths.

Sorption is quantified with mechanistic surface complexation models using the two-layer model of Dzombak and Morel (1990) as well as cation exchange (Hyun et al., 2001) following the bottom-up approach as described in Marques Fernandes et al. (2015) and Stockmann et al. (2017). The respective and proven dataset (Joseph et al., 2013a) with all surface parameters and reactions can be found in the Supplementary Materials of Hennig et al. (2020). In line with previous work (Bradbury and Baeyens, 2005a, b; Bradbury et al., 2005, 2010; Hartmann et al., 2008), sorption of uranium in the Opalinus Clay is modeled using only the clay minerals illite (Na-illite, Bradbury and Baeyens, 2005b) and montmorillonite (Na-montmorillonite, Bradbury and Baeyens, 2005a) as representative for the smectite group.

With the multi-component option in PHREEQC, diffusion is calculated individually for each species present in the system as sum of transport in the pore water as well as in the DDL via the electrochemical potential (Appelo and Wersin, 2007; Appelo et al., 2010; Parkhurst and Appelo, 2013). For this, PHREEQC uses the pore water diffusion coefficient D_p (m²/s), that is derived for each species analogous to Archie's law via the self-diffusion coefficient in water D_w (m²/s), the accessible porosity ϵ (–) and an empirical exponent n (-):

$$\begin{array}{}\text{(3)}& D_{\mathrm{p}}=D_{\mathrm{w}}\cdot {\mathit{ϵ}}^{\mathrm{n}}\end{array}$$

The exponent n is a constant, medium-specific parameter (Van Loon et al., 2007), that needs to be determined for the specific host rock. Hennig and Kühn (2021) calibrated their model by means of a diffusion experiment with uranium and Opalinus Clay (Joseph et al., 2013b). The best result was obtained for a value of n = 2.1, which we also used here. Anion exclusion is controlled by the amount of water in the DDL, derived here from the ionic strength (Wigger and Van Loon, 2018), and the water composition, which is calculated as average using the Donnan approximation implemented in PHREEQC (Parkhurst and Appelo, 2013). Further details on the model concept and the underlying equations can be found in Parkhurst and Appelo (2013), Appelo and Wersin (2007), Appelo et al. (2010), and Hennig and Kühn (2021).

Scenario 1 is in line with the PSI/Nagra database using the stability constant determined by Kalmykov and Choppin (2000) with a logk = 29.22, what leads to the predominance of the anionic complex ${\mathrm{CaUO}}_{\mathrm{2}}({\mathrm{CO}}_{\mathrm{3}}{)}_{\mathrm{3}}^{\mathrm{2}-}$, as already shown in Hennig et al. (2020). For Scenario 2, we have chosen the value obtained by Bernhard et al. (2001) with a logk = 30.55 since it was used for the speciation calculations in the diffusion experiment, on which the calibration of the parameter n is based (Joseph et al., 2013b).

3 Results

3.1 Pourbaix diagrams for the speciation of uranium

The Pourbaix diagrams were created using the pore water composition of the shaly facies (Table 1), that was initially equilibrated with the carbonates as well as pyrite for a pCO₂ of 10^−2.2 bar. From the Pourbaix diagrams, the predominant aqueous species can be read for a range of pH and pe conditions. In addition to the species shown in Fig. 1, the element under consideration, here uranium, can of course also be present in the form of further aquatic species in smaller proportion (Table 2). Speciation calculations were performed for standard pressure and temperature conditions (1 bar, 25 ^∘C) and a pH range from 2 to 10 as well as for E_H values between −413 mV and 413 mV corresponding to pe of −7 and 7, respectively. Figure 1a shows the aqueous speciation of uranium in the Opalinus Clay pore water of the shaly facies using the logk = 29.22 according to the PSI/Nagra database (Scenario 1), whereas in Fig. 1b the logk was exchanged by the value of 30.55 determined by Bernhard et al. (2001) (Scenario 2). The dashed box marks the pH and E_H range observed in the Opalinus Clay. The Pourbaix diagrams for the pore water composition of the sandy facies are identical with the ones shown in Fig. 1 and were already published in Hennig et al. (2020).

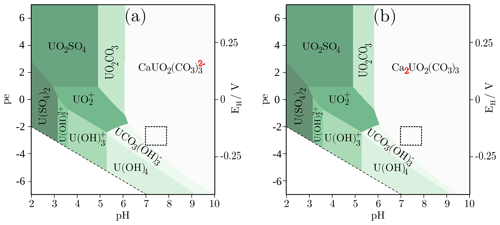
Figure 1 Pourbaix diagrams for the aqueous uranium speciation in the pore water of the shaly facies with an uranium background concentration of 2.52 µmol/L either using the logk = 29.22 given in the PSI/Nagra database (a) for the neutral, ternary uranyl complex or the value of 30.55 (b) obtained by Bernhard et al. (2001). The main change in speciation is highlighted by the red numbers. The pore water was initially equilibrated with the carbonates and pyrite for a pCO₂ of 10^−2.2 bar and calculations were performed for standard pressure and temperature conditions (1 bar, 25 ^∘C). The dashed box marks the pH and E_H range measured in-situ in the Opalinus Clay formation.

Table 2 Percentage of uranium species in the pore water of the shaly facies for the Scenario with logk = 29.22 (Scenario 1) and for the value of 30.55 (Scenario 2). Values of the sandy facies are given in brackets.

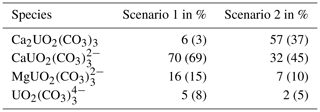
From Fig. 1 it becomes clear, that uranium is mainly present as U(VI) complexes with calcium and carbonate in the pH and pe range observed in the Opalinus Clay, whereby the chosen logk for the neutral, ternary uranyl complex governs uranium speciation in the modelled system. Depending on the selected value, either the ternary, anionic uranyl complex ${\mathrm{CaUO}}_{\mathrm{2}}({\mathrm{CO}}_{\mathrm{3}}{)}_{\mathrm{3}}^{\mathrm{2}-}$ (Scenario 1, Fig. 1a) is the predominant species or the neutral one Ca₂UO₂(CO₃)₃ (Scenario 2, Fig. 1b). A minor part (<2 %) is present as U(IV) as the in-situ conditions are close to the transition to the tetravalent state. Table 2 gives the distribution of uranium among the main species in the pore water of the shaly as well as sandy facies. The relative proportions of the species do not differ significantly (<1%) within the pH and E_H range marked by the dashed box in Fig. 1.

For Scenario 1, the percentage distribution of uranium among the individual species is similar in both facies. The main species is the anionic complex with calcium, followed by the anionic complex with magnesium ${\mathrm{MgUO}}_{\mathrm{2}}({\mathrm{CO}}_{\mathrm{3}}{)}_{\mathrm{3}}^{\mathrm{2}-}$ and minor parts of the neutral complex as well as ${\mathrm{UO}}_{\mathrm{2}}({\mathrm{CO}}_{\mathrm{3}}{)}_{\mathrm{3}}^{\mathrm{4}-}$. Whereas for the second Scenario, the proportion of the neutral complex increases in the sandy facies, but the anionic one is still the dominant. In the shaly facies, the neutral complex is predominant, as can be seen in Fig. 1b.

3.2 Uranium migration on the host rock scale

The difference of the uranium migration as a function of the predominant species was determined for the shaly and sandy facies of the Opalinus Clay by comparing the distances on the host rock scale (50 m) after a simulation time of one million years. Figure 2 shows the results for the shaly (Fig. 2a) and the sandy (Fig. 2b) facies, whereby Scenario 1 is represented by the solid line and Scenario 2 by the dashed line.

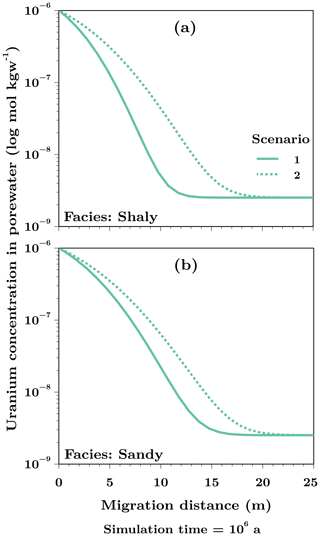
Figure 2 Uranium pore water concentrations in the shaly (a) and sandy facies (b) of the Opalinus Clay after a simulation time of one million years. The solid line shows the results for Scenario 1 using logk = 29.22 for the neutral, ternary uranyl complex and the dashed line represents the results for Scenario 2 with logk = 30.55.

For the two considered scenarios, migration distances of uranium varied after a simulation time of one million years between 13 m (Scenario 1) and 20 m (Scenario 2) in the shaly facies (Fig. 2a). In the sandy facies (Fig. 2b), it were 17 m (Scenario 1) and 22 m (Scenario 2). Thus, the difference between both scenarios and with that the influence of the predominant species on the maximum migration distance is stronger in the shaly facies. With a maximum distance of 22 m, uranium migrated the farthest in the sandy facies, although the difference to the shaly facies with a maximum of 20 m is only small.

4 Discussion

Based on the diffusion lengths of uranium after one million years, the influence of the stability constant for the neutral, ternary uranyl complex Ca₂UO₂(CO₃)₃ on the migration behaviour was quantififed with one-dimensional multi-component diffusion simulations in two scenarios and for different geochemical conditions as present in the shaly and sandy facies of the Opalinus Clay. For Scenario 1, the value according to the PSI/Nagra database (Thoenen et al., 2014) was chosen resulting in the anionic, ternary uranyl complex with calcium as predominant species (Fig. 1a) and less migration into the Opalinus Clay formation in both facies (solid line, Fig. 2) compared to Scenario 2. Here, a higher value determined by Bernhard et al. (2001) was applied and hence the thermodynamic equilibrium of the pore water was shifted towards the neutral, ternary uranyl complex as predominant species (Fig. 1b) with an associated farther migration of uranium. In metres, this means a difference between both scenarios of 7 and 5 m in the shaly and sandy facies, respectively.

The effect of anion exclusion hampers uranium migration. The predominant species in the modelled system, for instance anionic or neutral, governs the interaction with the DDL of the clay minerals. Due to their crystallographic structure, the surfaces of the clay minerals are negatively charged, what is compensated by the attraction of cationic species in the DDL and repulsion of anionic ones (Van Loon et al., 2003, 2007). This decreases the accessible (effective) pore space for anionic species leading to slower diffusion. Thus, the effect of anion exclusion explains the difference between the two investigated scenarios. The intensity of anion exclusion is thereby determined by the ionic strength of the pore water. With decreasing ionic strength, the thickness of the DDL increases and hence the effect of anion exclusion (Wersin et al., 2008, 2018; Wigger and Van Loon, 2018). This in turn implies, that the difference in migration length between the two scenarios should be greater for the sandy facies with the lower ionic strength and associated thicker DDL compared to the shaly (Table 1). However, unlike our expectations, we observed the opposite. This means, additional factors also play a role as the difference between the scenarios for the two facies shows.

Calcium concentration in the pore water, and hence the geochemical composition itself, controls uranium speciation stronger than selection of thermodynamic data. From previous numerical studies we know, that the pore water composition, mainly pCO₂ and calcium concentration, and with that the geochemical conditions in the facies of the Opalinus Clay govern uranium sorption (Hennig et al., 2020) and transport processes (Hennig and Kühn, 2021). This also applies here. Due to the lower initial calcium concentration in the sandy compared to the shaly facies (Table 1), the thermodynamic equilibrium of the pore water results in a governing anionic complex, even for Scenario 2. It is simply not enough calcium present in solution to completely shift the species distribution towards the neutral complex, as twice as much is required to form the complex. This is also reflceted by the aqueous species distribution of uranium for Scenario 2 in the sandy facies (values in brackets, Table 2). Therefore, the variant influence of the stability constant on the uranium migration lengths is explained by the major differences of the pore water composition for the two facies.

With the second update on the chemical thermodynamics of uranium of the NEA (Grenthe et al., 2020), the discussion about the value for the stability constant of the neutral, ternary complex Ca₂UO₂(CO₃)₃ was settled. Within this review, new studies have been discussed and evaluated and the logk of Endrizzi and Rao (2014) with a value of 30.8 has been selected as the most precise one published to-date. This value is even higher as the one of Bernhard et al. (2001) used for scenario 2 (logk = 30.55). This in turn means for uranium speciation in the geochemical system of the Opalinus Clay, that the neutral, ternary complex is the predominant one and migration lengths of uranium correspond more to the results of scenario 2 or probably even greater.

5 Conclusions

The influence of data selection for the underlying chemical database on the diffusion length in the Swiss Opalinus Clay was tested using the example of the thermodynamic data for uranium. As required for safety assessments of potential repositories, the migration distance after one million years, was quantified for the host rock scale. We have investigated the effect of two different values for the thermodynamic stability constant of a predominant uranium species as given in the literature. Our speciation calculations have shown, that uranium is mostly present as U(VI) with calcium and carbonate. Depending on the chosen value for the stability constant of the neutral, ternary uranyl complex Ca₂UO₂(CO₃)₃, the predominant species in the pH and pe range observed in the Opalinus Clay is either the neutral or the anionc complex ${\mathrm{CaUO}}_{\mathrm{2}}({\mathrm{CO}}_{\mathrm{3}}{)}_{\mathrm{3}}^{\mathrm{2}-}$. Hence, with our multi-component diffusion simulations accounting for the interaction of different charged species with the diffuse double layers (DDL) enveloping the clay minerals, we wanted to answer the question: What does the uncertainty regarding the thermodynamic data mean in metre of the migration distance on the host rock scale (50 m) after one million years? For this, we set up two scenarios identical except for the applied value for the stability constant of the neutral complex.

Simulations were performed for the shaly and sandy facies representing main differences in the pore water composition and clay mineral content as it has been shown, that uranium migration and sorption is mainly governed by the present geochemical conditions, namely pCO₂, calcium concentration, pH and pe, and less by the quantity of clay minerals. Uranium sorption on the clay minerals is decreased due to the formation of ternary complexes with calcium, magnesium and carbonate. Hence, the geochemical system in the facies is controlled by a fixed pCO₂ of 10^−2.2 bar and mineral equilibria with the carbonates (calcite, dolomite and siderite) as well as pyrite governing the concentrations of the main ions, pH and pe.

For the shaly facies, maximum migration distances after one million years were 13 m (Scenario 1, logk = 29.22) and 20 m (Scenario 2, logk = 30.55) for the scenario with the anionic and neutral complex as predominant species, respectively. In the sandy facies, the diffusion lengths were 17 and 22 m, correspondingly. The difference in the migration lengths of the two considered scenarios can be explained by the effect of anion exclusion and hence by the predominant species. Due to the negatively charged surfaces of the clay minerals, anions are excluded from the DDL and thus their accessible pore space and so their diffusive transport are diminished. Consequently, the larger the proportion of the anionic complex, the more is uranium diffusion through the facies hampered by the anion exclusion effect. The intensity of anion exclusion depends thereby on ionic strength as it governs the amount of water in the DDL. A lower ionic strength as in the sandy facies, for instance, is associated with a thicker DDL and thus stronger anion exclusion. Accordingly, the difference between the two scenarios should potentially be the largest in the sandy facies. However, the influence of the stability constant on the migration lengths and thus on the difference between the two scenarios is less in the sandy facies compared to the shaly facies. Due to the lower initial calcium concentration in the sandy facies, the anionic complex is predominant for both scenarios.

With this, we quantified the effect of the stability constant of the Ca₂UO₂(CO₃)₃ complex on the maximum diffusion length of uranium and demonstrated, what a difference of 1.33 log units means in metre on the host rock scale, e.g. 5 and 7 m for the sandy and shaly facies, respectively. However, as uranium is still retained within the formation with a thickness of around 160 m and no adjacent aquifer is reached, the effect is negligible in the geochemical system of the Opalinus Clay for the host rock scale. Furthermore, our results can serve as reference for clay formations with similar geochemistry, in case that speciation of uranium and thus migration is dominated by calcium and carbonate.