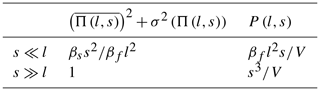On the Density Variability of Poissonian Discrete Fracture Networks, with application to power-law fracture size distributions

This paper presents analytical solutions to estimate at any scale the fracture density variability associated to stochastic Discrete Fracture Networks. These analytical solutions are based upon the assumption that each fracture in the network is an independent event. Analytical solutions are developed for any kind of fracture density indicators. Those analytical solutions are verified by numerical computing of the fracture density variability in three-dimensional stochastic Discrete Fracture Network (DFN) models following various orientation and size distributions, including the heavy-tailed power-law fracture size distribution. We show that this variability is dependent on the fracture size distribution and the measurement scale, but not on the orientation distribution. We also show that for networks following power-law size distribution, the scaling of the three-dimensional fracture density variability clearly depends on the power-law exponent.

1 Introduction

Characterizing fracture networks in geosciences is a key challenge for many industrial projects such as deep waste disposal, hydrogeology or petroleum resources, because it may change the mechanical (Davy et al., 2018; Grechka and Kachanov, 2006) and hydrological (Bogdanov et al., 2007; De Dreuzy et al., 2001a, b) behaviour of the rock mass. Fractures being ubiquitous and at all scales, the description of these physical properties is often far beyond the reach of a continuum approach (Jing, 2003). Discrete Fracture Networks are computational models explicitly representing the geometry of fractures in a network, and can be used as a basis for physical simulations (mechanical strength, flow, transport…) (see Jing, 2003; Lei et al., 2017, for a review). Considering the scarce nature of geological data, statistical methods have been widely used to generate DFN models, where all fracture geometrical attributes are treated as independent variables from probability distribution derived from the field. Indeed, fracture networks are often described from size distribution, sets of orientations, location, and densities (Dershowitz and Einstein, 1988). Unfortunately, the difficulty of access and resolution to volumetric data makes it difficult to directly measure three-dimensional fracture densities. Stereological analysis proposes theoretical relationship to calculate the 3-D density from 1-D or 2-D measurements under some assumptions (Berkowitz and Adler, 1998; Darcel et al., 2003a; Warburton, 1980). For example, the total fracture surface per unit volume p₃₂ can be calculated from one-dimensional fracture intersections along scanlines or boreholes using some conversion factor (Mauldon, 1994; Terzaghi, 1965; Wang, 2005). Most of these studies focus on characterizing the mean density of a fractured system with poor interest to the underlying variability. However, fracture density variability is an indicator for fracture clustering, which may have dramatical impact on connectivity (Darcel et al., 2003b; La Pointe, 1988; Manzocchi, 2002). Darcel et al. (2013) proposed an analytical solution to quantify at any scale, the standard deviation associated to fracture frequency p₁₀, considering fracture-borehole crossing as a one-dimensional Poisson point process (random positions with fixed density). They show that the standard deviation associated to the number of intersections per unit length p₁₀ is inversely proportional to the square root of the measurement scale. This solution was also demonstrated by Lu et al. (2017), who validated it numerically computing p₁₀ values on boreholes crossing three-dimensional Poissonian DFN models of fixed fracture density. In this paper, we aim to develop analytical solutions for three-dimensional Poissonian DFN models to quantify the range of variability of any kind of fracture density, of any dimension. Particularly, we propose solutions for three-dimensional density variability that cannot be obtained directly from the field. We show that this variability depends on the measurement scale and the fracture size distribution, but not on the orientation distribution. These solutions are validated by numerical simulations, computing the associated fracture densities mean and variance at various scales for three-dimensional Poissonian Discrete Fracture Networks.

2 Theoretical development

In the following, we will calculate the variability of the fracture densities p_Dd such as defined by Dershowitz and Herda (1992) and Mauldon and Dershowitz (2000). D and d refers to the dimensions of the embedding system Σ and of the fracture trace in Σ, respectively, so that d≤D. For instance, p₁₀ is the number of intersection points (d=0) along a line (D=1) per unit line size. We denote by μ_f the contribution of a fracture f to p_Dd (μ_f is a d-dimension measure) and s the scale at which p_Dd and μ_f are calculated so that:

$$\begin{array}{}\text{(1)}& p_{Dd}={\displaystyle \frac{{\sum }_f{\mathit{\mu }}_f\left(s\right)}{s^D}},\end{array}$$

First, we calculate the spatial variability of the measure μ_f(s) calculated in a D-sphere of size s embedded in a larger space Σ of volume V. In D-dimension, a fracture is represented by an object of dimension D−1 (a point in a scanline, a line in a 2-D outcrop, or a surface in the 3-D space) with a size S_f. The proportion of the total volume occupied by the fracture – i.e., the volume where the measure μ_f(s) is not nil – is:

$$\begin{array}{}\text{(2)}& P_f\left(s\right)=\left\{\begin{array}{cc}\frac{S_f\cdot s}{V},& S_f>s^{D-\mathrm{1}}\\ \frac{s^D}{V},& S_f<s^{D-\mathrm{1}}\end{array}\right.,\end{array}$$

We then assume that, when it is not nil, the measure μ_f(s) derives from a distribution with a mean $\stackrel{\mathrm{‾}}{{\mathit{\mu }}_{f,s}}$ and a standard deviation ${\mathit{\sigma }}_{{\mathit{\mu }}_{f,s}}$. For the total system, we can calculate the first and second order moment of μ_f(s):

$$\begin{array}{}\text{(3a)}& {\displaystyle }\langle {\mathit{\mu }}_f\rangle =P_f\left(s\right)\cdot \stackrel{\mathrm{‾}}{{\mathit{\mu }}_{f,s}},\text{(3b)}& {\displaystyle }\langle {\mathit{\mu }}_f^{\mathrm{2}}\rangle =P_f\left(s\right)\cdot \left({\stackrel{\mathrm{‾}}{{\mathit{\mu }}_{f,s}}}^{\mathrm{2}}+{\mathit{\sigma }}_{{\mathit{\mu }}_{f,s}}^{\mathrm{2}}\right),\end{array}$$

The variance σ²(μ_f) is written as:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\mathit{\sigma }}^{\mathrm{2}}\left({\mathit{\mu }}_f\right)& =\langle {\mathit{\mu }}_f^{\mathrm{2}}\rangle -\langle {\mathit{\mu }}_f{\rangle }^{\mathrm{2}}\\ & =P_f\left(s\right)\left(\mathrm{1}-P_f\left(s\right)\right)\cdot {\stackrel{\mathrm{‾}}{{\mathit{\mu }}_f}}^{\mathrm{2}}+P_f\left(s\right){\mathit{\sigma }}_{{\mathit{\mu }}_{f,s}}^{\mathrm{2}},\end{array}\end{array}$$

We now sum the contribution of all fractures to calculate $\mathit{\mu }\left(s\right)={\sum }_f{\mathit{\mu }}_f\left(s\right)$. With the Poisson's hypothesis, all fractures are independent events and the variance σ²(μ) is the sum of the variance of each fracture:

$$\begin{array}{}\text{(5)}& {\mathit{\sigma }}^{\mathrm{2}}\left(\mathit{\mu }\right)={\mathit{\sigma }}^{\mathrm{2}}\left({\sum }_f{\mathit{\mu }}_f\right)={\sum }_f{\mathit{\sigma }}^{\mathrm{2}}\left({\mathit{\mu }}_f\right),\end{array}$$

And finally, the variability of the density measure p_Dd is ${\mathit{\sigma }}^{\mathrm{2}}\left(p_{Dd}\right)={\mathit{\sigma }}^{\mathrm{2}}\left(\mathit{\mu }\right)/s^{\mathrm{2}D}$. In the following, we compute the dimensionless ratio between the variance σ²(p_Dd) and the square of the mean $\stackrel{\mathrm{‾}}{p_{Dd}}$:

$$\begin{array}{}\text{(6)}& \mathit{\lambda }\left(p_{Dd}\right)={\left[{\displaystyle \frac{\mathit{\sigma }\left(p_{Dd}\right)}{\stackrel{\mathrm{‾}}{p_{Dd}}}}\right]}^{\mathrm{2}},\end{array}$$

In the fractal theory, λ(⋅) is called lacunarity (Plotnick et al., 1996). This is a scale dependent measure, whose analysis gives an idea of the scaling of fracture network textural heterogeneity and potentially on different regimes (Plotnick et al., 1996; Roy et al., 2014).

For geological environments, fracture networks are characterized by a wide distribution of fracture sizes. We denote by n(l) the density distribution of fracture sizes, and n(l)dl is the number of fractures of size in the range $[l,l+dl]$ per system volume (Davy, 1993). The total number of fractures in a system of volume V is $N=V\int n\left(l\right)dl$ . We then assume that the measure μ_f(s) and the occupied volume ratio P_f(s) only depends on the fracture size l so that ${\mathit{\mu }}_f\left(s\right)=\mathit{\mu }(l,s)$ and $P_f\left(s\right)=P(l,s)$. Equation (6) can now be written as a function of the fracture size distribution:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}& \mathit{\lambda }\left(p_{Dd}\right)=\\ & {\displaystyle \frac{V}{{\stackrel{\mathrm{‾}}{p_{Dd}}}^{\mathrm{2}}}}{\displaystyle \frac{\int \left({\displaystyle \begin{array}{c}P\left(l,s\right)\cdot \left[\mathrm{1}-P\left(l,s\right)\right]\cdot {\stackrel{\mathrm{‾}}{\mathit{\mu }\left(l,s\right)}}^{\mathrm{2}}\\ +P\left(l,s\right)\cdot {\mathit{\sigma }}^{\mathrm{2}}\left(\mathit{\mu }\left(l,s\right)\right)\end{array}}\right)\cdot n\left(l\right)dl}{s^{\mathrm{2}D}}},\end{array}\end{array}$$

In the following, we especially focus on the power-law size distribution, which have been found to adequately fit natural systems (Bonnet et al., 2001; Bour, 2002; Bour and Davy, 1999; Odling, 1997):

$$\begin{array}{}\text{(8)}& n\left(l\right)=\mathit{\alpha }\cdot l^{-a},\end{array}$$

with a the power-law exponent, α the density term.

2.1 1-D measurements

Fracture abundance is often quantified on boreholes using the one-dimensional fracture frequency p₁₀ measurement, defined as the number N of crossing fractures per unit borehole length L. If a fracture intersecting this borehole is also part of a subsample of size s, the associated measure $\mathit{\mu }(l,s)=\mathrm{1}$. The ratio of subsamples intersected by this fracture is $P\left(l,s\right)=s/L$. Considering that s≪L, then $P\left(l,s\right)\ll \mathrm{1}$, and the lacunarity of such measurement is the one of a one-dimensional Poisson point process (Darcel et al., 2013; Lu et al., 2017):

$$\begin{array}{}\text{(9)}& {\mathit{\lambda }}_{p_{\mathrm{10}}}\left(s\right)={\displaystyle \frac{\mathrm{1}}{{\stackrel{\mathrm{‾}}{p_{\mathrm{10}}}}^{\mathrm{2}}}}{\displaystyle \frac{N(s/L)}{s^{\mathrm{2}}}}={\displaystyle \frac{\mathrm{1}}{\stackrel{\mathrm{‾}}{p_{\mathrm{10}}}}}{s}^{-\mathrm{1}},\end{array}$$

2.2 3-D measurements

In three-dimensional systems, the fractures d-measures μ_f are either their occurrence (d=0), surface (d=2) or surrounded sphere (d=3). μ_f(s) such as defined in the previous section is the part of the measure μ_f that is included into a domain S of size s, that is the product of μ_f by the occurrence probability of the fracture to be included into the domain S, Π_f,s (also noted Π(l,s) following the notation of the previous section). We define Π_f,s as the ratio between the fracture surface included into the domain S to the total fracture surface. If the fracture size is larger than s, both the average value of Π_f,s and its standard deviation are proportional to the surface s². If $P\left(l,s\right)\ll \mathrm{1}$, that is for large systems, Eqs. (4) and (7) requires to know the expression of ${\left(\stackrel{\mathrm{‾}}{\mathrm{\Pi }\left(l,s\right)}\right)}^{\mathrm{2}}+{\mathit{\sigma }}^{\mathrm{2}}\left(\mathrm{\Pi }\left(l,s\right)\right)$. The scaling of ${\left(\stackrel{\mathrm{‾}}{\mathrm{\Pi }\left(l,s\right)}\right)}^{\mathrm{2}}+{\mathit{\sigma }}^{\mathrm{2}}\left(\mathrm{\Pi }\left(l,s\right)\right)$ and P(l,s) are given in Table 1, with β_s and β_f shape factors depending on domain S and fractures geometries respectively. This binary model will allow us to simplify the analytical solutions, although we may have significant errors when l∼s.

Table 1 Scaling of parameters ${\left(\stackrel{\mathrm{‾}}{\mathrm{\Pi }\left(l,s\right)}\right)}^{\mathrm{2}}+{\mathit{\sigma }}^{\mathrm{2}}\left(\mathrm{\Pi }\left(l,s\right)\right)$ and P(l,s).

2.2.1 Fracture number density p₃₀

The p₃₀ measure counts the number of fractures N per unit volume V. Fracture occurrence can be measured as $\mathit{\mu }\left(l,s\right)=\mathrm{\Pi }\left(l,s\right)$. The corresponding lacunarity ${\mathit{\lambda }}_{p_{\mathrm{30}}}$ under our hypothesis is then given by:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}& {\mathit{\lambda }}_{p_{\mathrm{30}}}\left(s\right)=\\ & {\displaystyle \frac{V}{{\stackrel{\mathrm{‾}}{p_{\mathrm{30}}}}^{\mathrm{2}}}}{\displaystyle \frac{\int P\left(l,s\right)\cdot \left[{\left(\stackrel{\mathrm{‾}}{\mathrm{\Pi }\left(l,s\right)}\right)}^{\mathrm{2}}+{\mathit{\sigma }}^{\mathrm{2}}\left(\mathrm{\Pi }\left(l,s\right)\right)\right]\cdot n\left(l\right)dl}{s^{\mathrm{6}}}},\end{array}\end{array}$$

If we consider that fractures have all the same size l_f, then:

$$\begin{array}{}\text{(11)}& {\mathit{\lambda }}_{p_{\mathrm{30}}}\left(s\right)=\left\{\begin{array}{ll}({\mathit{\beta }}_s^{\mathrm{2}}/\stackrel{\mathrm{‾}}{p_{\mathrm{32}}})\cdot s^{-\mathrm{1}},& s\ll l_f\\ (\mathrm{1}/\stackrel{\mathrm{‾}}{p_{\mathrm{30}}})\cdot s^{-\mathrm{3}},& s\gg l_f\end{array}\right.\end{array}$$

If we consider now that the network follows a power-law size distribution with minimum and maximum fracture size l_min and l_max, the p₃₀ lacunarity equation is defined by three regimes:

$$\begin{array}{}\text{(12)}& {\mathit{\lambda }}_{p_{\mathrm{30}}}\left(s\right)=\left\{\begin{array}{ll}\left(\frac{\mathit{\alpha }}{{\stackrel{\mathrm{‾}}{p_{\mathrm{30}}}}^{\mathrm{2}}}\frac{{\mathit{\beta }}_s^{\mathrm{2}}}{{\mathit{\beta }}_f}{\int }_{l_{min}}^{l_{max}}{l}^{-\left(a+\mathrm{2}\right)}dl\right)s^{-\mathrm{1}},& s\ll l_{min}\\ \frac{\mathit{\alpha }}{{\stackrel{\mathrm{‾}}{p_{\mathrm{30}}}}^{\mathrm{2}}}\left(s^{-\mathrm{3}}{\int }_{l_{min}}^s{l}^{-a}dl\right.& \\ \left.+\frac{{\mathit{\beta }}_s^{\mathrm{2}}}{{\mathit{\beta }}_f}{s}^{-\mathrm{1}}{\int }_s^{l_{max}}{l}^{-(a+\mathrm{2})}dl\right),& s\in [l_{min},l_{max}]\\ (\mathrm{1}/\stackrel{\mathrm{‾}}{p_{\mathrm{30}}})\cdot s^{-\mathrm{3}},& s\gg l_{max}\end{array}\right.\end{array}$$

2.2.2 Fracture intensity p₃₂

Fracture intensity p₃₂ measures the total fracture surface per unit volume. The contribution of each fracture of size l in the domain S is $\mathit{\mu }\left(l,s\right)=\mathrm{\Pi }\left(l,s\right){\mathit{\beta }}_f{l}^{\mathrm{2}}$. The corresponding lacunarity ${\mathit{\lambda }}_{p_{\mathrm{32}}}$ is then given by:

$$\begin{array}{}\text{(13)}& \begin{array}{rl}& {\mathit{\lambda }}_{p_{\mathrm{32}}}\left(s\right)=\\ & {\displaystyle \frac{{\mathit{\beta }}_f^{\mathrm{2}}}{{\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}}^{\mathrm{2}}}}{\displaystyle \frac{\int P\left(l,s\right)\cdot \left[{\left(\stackrel{\mathrm{‾}}{\mathrm{\Pi }\left(l,s\right)}\right)}^{\mathrm{2}}+{\mathit{\sigma }}^{\mathrm{2}}\left(\mathrm{\Pi }\left(l,s\right)\right)\right]\cdot l^{\mathrm{4}}\cdot n\left(l,L\right)dl}{s^{\mathrm{6}}}},\end{array}\end{array}$$

Following the same reasoning as for p₃₀ density, if we consider that all fractures have the same size l_f, we find that the p₃₂ lacunarity ${\mathit{\lambda }}_{p_{\mathrm{32}}}$ follows Eq. (11). If we consider now that the network follows a power-law size distribution, the p₃₂ lacunarity equation is defined by three regimes:

$$\begin{array}{}\text{(14)}& {\mathit{\lambda }}_{p_{\mathrm{32}}}\left(s\right)=\left\{\begin{array}{ll}({\mathit{\beta }}_s^{\mathrm{2}}/\stackrel{\mathrm{‾}}{p_{\mathrm{32}}})\cdot s^{-\mathrm{1}},& s\ll l_{min}\\ \frac{\mathit{\alpha }}{{\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}}^{\mathrm{2}}}\left({\mathit{\beta }}_f^{\mathrm{2}}{s}^{-\mathrm{3}}{\int }_{l_{min}}^s{l}^{\mathrm{4}-a}dl\right.& \\ \left.+{\mathit{\beta }}_f{\mathit{\beta }}_s^{\mathrm{2}}{s}^{-\mathrm{1}}{\int }_s^{l_{max}}{l}^{\mathrm{2}-a}dl\right),& s\in [l_{min},l_{max}]\\ (\mathrm{1}/\stackrel{\mathrm{‾}}{p_{\mathrm{30}}})\cdot s^{-\mathrm{3}}& s\gg l_{max}\end{array}\right.\end{array}$$

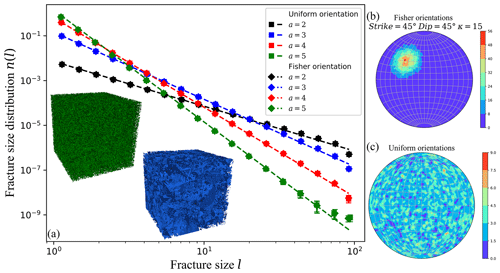
Figure 1 (a) Fracture size distribution of generated networks sets (3–6) following power-law size distribution with a bulk density $\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}=\mathrm{0.5}$ and different power-law exponent a indicated in the legend box (a=3 in blue, a=5 in green), and (b)–(c) stereonets for the two defined orientation distributions.

Figure 2 Theoretical (dash) and experimental (dots) p₁₀ lacunarity curves for fracture network sets (3–6) following power-law size distribution at bulk density $\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}=\mathrm{0.5}$.

2.2.3 Percolation parameter p

The percolation parameter gives an idea of the connectivity of the network (Bour and Davy, 1997, 1998; Robinson, 1983). Fundamentally, it is total excluded volume around fractures per unit volume so that for disk-shaped fractures the associated measure $\mathit{\mu }(l,s)=({\mathit{\pi }}^{\mathrm{2}}/\mathrm{8})\cdot \mathrm{\Pi }\left(l,s\right)l^{\mathrm{3}}$ (De Dreuzy et al., 2000). The corresponding lacunarity λ_p is then given by:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}& {\mathit{\lambda }}_p\left(s\right)=\\ & {\displaystyle \frac{{\mathit{\pi }}^{\mathrm{4}}}{\mathrm{64}}}{\displaystyle \frac{V}{{\stackrel{\mathrm{‾}}{p}}^{\mathrm{2}}}}{\displaystyle \frac{\int P\left(l,s\right)\cdot \left[{\left(\stackrel{\mathrm{‾}}{\mathrm{\Pi }\left(l,s\right)}\right)}^{\mathrm{2}}+{\mathit{\sigma }}^{\mathrm{2}}\left(\mathrm{\Pi }\left(l,s\right)\right)\right]\cdot l^{\mathrm{6}}\cdot n\left(l\right)dl}{s^{\mathrm{6}}}},\end{array}\end{array}$$

If we consider that all fractures have the same size l_f, then:

$$\begin{array}{}\text{(16)}& {\mathit{\lambda }}_p\left(s\right)=\left\{\begin{array}{ll}(\mathrm{1}/\stackrel{\mathrm{‾}}{p_{\mathrm{30}}})\cdot s^{-\mathrm{3}},& s\ll l_f\\ \frac{{\mathit{\pi }}^{\mathrm{2}}}{\mathrm{8}}.\frac{{\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}}^{\mathrm{2}}}{\stackrel{\mathrm{‾}}{p}\cdot \stackrel{\mathrm{‾}}{p_{\mathrm{30}}}}\cdot \frac{{\mathit{\beta }}_s^{\mathrm{4}}}{{\mathit{\beta }}_f^{\mathrm{3}}}\cdot s^{-\mathrm{1}},& s\gg l_f\end{array}\right.\end{array}$$

If fracture size distribution follows a power-law size distribution, the percolation parameter lacunarity becomes:

$$\begin{array}{}\text{(17)}& {\mathit{\lambda }}_p\left(s\right)=\left\{\begin{array}{ll}\left(\frac{\mathit{\alpha }}{{\stackrel{\mathrm{‾}}{p}}^{\mathrm{2}}}\cdot \frac{{\mathit{\pi }}^{\mathrm{4}}}{\mathrm{64}}\cdot \frac{{\mathit{\beta }}_s^{\mathrm{2}}}{{\mathit{\beta }}_f}{\int }_{l_{min}}^{l_{max}}{l}^{\mathrm{4}-a}dl\right)\cdot s^{-\mathrm{1}},& s\ll l_{min}\\ \frac{{\mathit{\pi }}^{\mathrm{2}}}{\mathrm{8}}\frac{\mathit{\alpha }}{{\stackrel{\mathrm{‾}}{p}}^{\mathrm{2}}}(s^{-\mathrm{3}}{\int }_{l_{min}}^s{l}^{\mathrm{6}-a}dl+\frac{{\mathit{\beta }}_s^{\mathrm{4}}}{{\mathit{\beta }}_f^{\mathrm{3}}}{s}^{-\mathrm{1}}& \\ {\int }_s^{l_{max}}{l}^{\mathrm{4}-a}dl),& s\in [l_{min},l_{max}]\\ \left(\frac{\mathit{\alpha }}{{\stackrel{\mathrm{‾}}{p}}^{\mathrm{2}}}\cdot \frac{{\mathit{\pi }}^{\mathrm{4}}}{\mathrm{64}}{\int }_{l_{min}}^{l_{max}}{l}^{\mathrm{6}-a}dl\right)\cdot s^{-\mathrm{3}},& s\gg l_{max}\end{array}\right.\end{array}$$

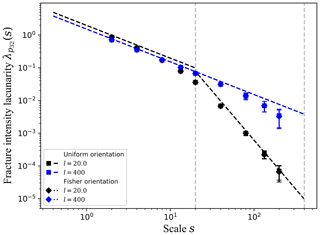
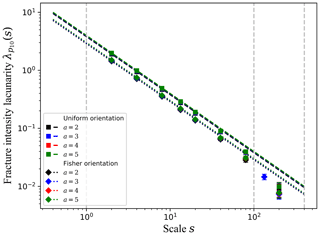
Figure 3 Fracture intensity lacunarity curves ${\mathit{\lambda }}_{p_{\mathrm{32}}}$ for networks with constant fracture size and bulk density $\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}=\mathrm{0.5}$.

Figure 4 Fracture densities lacunarity curves (a) ${\mathit{\lambda }}_{p_{\mathrm{30}}}\left(s\right)$, (b) ${\mathit{\lambda }}_{p_{\mathrm{32}}}\left(s\right)$, (c) λ_p(s) for networks following power-law fracture size distributions with total fracture intensity $\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}=\mathrm{0.5}$, and (d) evolution of fracture intensity lacunarity ${\mathit{\lambda }}_{p_{\mathrm{32}}}$ at fixed scale (s=20) with fracture bulk intensity $\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}$.

3 Density variability of DFN with power-law size distributions and various orientation distribution

In this section, we aim at validating the analytical solutions developed in Sect. 2, with numerical experiments on Discrete Fracture Networks (DFN). We generate some very simple Poissonian DFN models where the position of each fracture is set randomly within a cubic system of size L=400, and other fracture parameters (orientations, size…) are picked up in the corresponding distribution independently of each other. The fracture shapes are disks, and the diameters l are either constant or power-law distributed. In order to minimize finite-size effects, fracture centers are generated in a cubic box system of size $\left(L+l_{max}\right)$ with l_max the largest fracture. We here define two fracture network sets with constant size: (1) $l_f=\mathrm{20}\ll L$ and (2) $l_f=L=\mathrm{400}$. We also define four fracture network sets (3, 4, 5, 6) following power-law size distribution with $l_{min}=\mathrm{1}$, $l_{max}=\mathrm{100}$, and where the power-law exponent a is within the range [2,5]. All network sets are simulated for different fracture intensities $p_{\mathrm{32}}\in \mathit{\{}\mathrm{0.1},\mathrm{0.2},\mathrm{0.3},\mathrm{0.4},\mathrm{0.5}\mathit{\}}$. We test two different fracture orientation distributions: (a) uniform, all orientations are equally represented, (b) Fisher distribution f(θ,κ) (Fisher, 1953) with a mean pole θ defined by a strike and dip angle both of 45^∘, and a dispersion factor κ=15. For statistical analysis, we perform 50 realizations of each fracture sets. Figure 1 shows examples of generated networks and their associated size distributions.

3.1 1-D measurements

We compute the p₁₀ lacunarity curves on 81 boreholes crossing the whole domain, equally spaced and parallel to the z direction, divided in subsamples of size $s\in [\mathrm{0.02}L,L]$ with no overlap. The general p₁₀ lacunarity curve of the system is obtained by stacking the contribution of each borehole. Figure 2 shows that the lacunarity curves associated to the generated Poissonian DFN models with power-law size distribution and mean density $\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}$ follow Eq. (9) as predicted by Darcel et al. (2013) and Lu et al. (2017). When s∼L, the lacunarity curve drops down because of finite-size effects. Lacunarity curves are not the same for the uniform and the Fisher orientation distributions, because the $\stackrel{\mathrm{‾}}{p_{\mathrm{10}}}$ densities are not the same. Indeed, for the same p₃₂ density, the p₁₀ value measured on a borehole depends of the relative orientation between fractures and the borehole. For uniform orientation $p_{\mathrm{10}}=p_{\mathrm{32}}/\mathrm{2}$, and for the defined Fisher orientation p₁₀=0.75p₃₂ which can be found from Wang (2005) formulae.

3.2 3-D measurements

To construct the experimental three-dimensional density lacunarity curves, we divide the cubic domain of size L in L³∕s³ subdomains with no overlap at different scales s. On each subdomain, the three-dimensional fracture densities defined in Sect. 2.2 (p₃₀, p₃₂, p) are computed numerically in order to obtain the associated mean and standard deviation over the whole domain at scale s, giving access to the corresponding lacunarities. For the analytical analysis, we consider that the fracture disk shape factor is ${\mathit{\beta }}_f=\mathit{\pi }/\mathrm{4}$, and that the subdomain shape factor is β_s=1. Figure 3 focuses on the p₃₂ lacunarity of constant size fracture networks with total fracture intensity $\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}=\mathrm{0.5}$. For the case where the fracture size l_f=20, Eq. (10) shows two asymptotes for the experimental lacunarity curves for s≪l_f and for s≫l_f, respectively. When s∼l_f, the equations overpredict the lacunarity by a factor of at most 3.

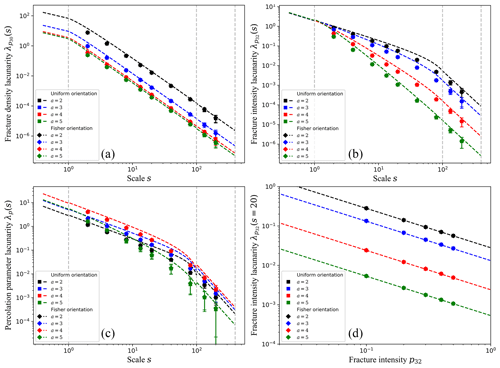
Figure 4 focuses on various 3-D density lacunarity curves for networks following power-law size distributions. When the study scale s is larger than the minimum fracture size l_min, the p₃₀ lacunarity curves (Fig. 4a) evolves as a three-dimensional binomial process ($\sim s^{-\mathrm{3}}$), which is coherent with the fact that fractures are positioned randomly in space. The fracture intensity lacunarity ${\mathit{\lambda }}_{p_{\mathrm{32}}}$ and percolation parameter lacunarity λ_p (Fig. 4b and c respectively), are divided in three different regimes. When we investigate the dependence upon the scale $s\in \left[l_{min},l_{max}\right]$, their scaling clearly depends of the power-law size distribution exponent a. For large a values (a≥5), the p₃₂ lacunarity curve scales as $\sim s^{-\mathrm{3}}$ because small fractures are dominant. For this range of study scale, we can notice a slight discrepancy between the analytical solutions and the numerical experiments. The lower a the larger this discrepancy. This can be explained by the fact that for low a values, the number of fractures whose size l∼s is always significant. Nevertheless, these analytical solutions reproduce well the observed scaling of fracture densities lacunarity. At scale $s\sim l_{max}$, the difference of p₃₂ lacunarity between networks following either a power-law size distribution of exponent a=2 or a=5 vary up to a factor 10³. Finally, Fig. 4d analyses ${\mathit{\lambda }}_{p_{\mathrm{32}}}$ at fixed scale s=20 for different bulk $\stackrel{\mathrm{‾}}{p_{\mathrm{32}}}$ values, highlighting that fracture density lacunarity is inversely proportional to the total fracture density. Finally, for any fracture density, all lacunarity curves are identical whatever the fracture orientation distribution (uniform or Fisher), which proves the orientation independency.

4 Conclusion

We propose here analytical solutions to quantify the density variability associated to Poissonian fracture networks, using the dimensionless variance parameter λ that we call lacunarity. Solutions are demonstrated for any kind of fracture density of any dimension, with application to uniform and power-law size distribution. The application to other fracture size distribution (exponential, log-normal…) is straightforward. These analytical solutions were validated numerically by computing the density variability on Poissonian DFN models for different bulk density values, fracture size and orientation distributions. We show that the variability of three-dimensional densities is dependent on the study scale and the fracture size distribution, but not on the orientation distribution. Moreover, we show that for networks following power-law size distributions, the scaling of the variability of the fracture intensity p₃₂ is strongly dependent of this power-law exponent. This suggest that the variability of p₃₂ density cannot be estimated from borehole p₁₀ measurements, as it is done to quantify the mean p₃₂ density over the whole network using simple stereological rules. These solutions, which are developed for purely stochastic networks, can thus be used as a reference to estimate three-dimensional fracture density variability on the field, which is out of reach of our investigation technics. Further work is ongoing to quantify the fracture density variability for networks showing fractal correlations (Darcel et al., 2003b), which may also be quantified from the field. We expect the clustering effect associated to such networks to increase significantly the variability of fracture densities and its scaling.